ОПРЕДЕЛЕНИЕ ОБЪЕМОВ ТЕЛ ВРАЩЕНИЯ ВОКРУГ ОСИ ОРДИНАТ С ПОМОЩЬЮ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Секция: Физико-математические науки

LXXII Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
ОПРЕДЕЛЕНИЕ ОБЪЕМОВ ТЕЛ ВРАЩЕНИЯ ВОКРУГ ОСИ ОРДИНАТ С ПОМОЩЬЮ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Аннотация. Статья направлена на изучение способов вычисления объемов тел вращения плоских фигур вокруг оси ординат. Объемы тел вращения, как известно, вычисляются с применением двойного или тройного интегралов. В данной статье предлагается вычислить объем тела вращения вокруг оси ординат лишь с помощью определенного интеграла.
Ключевые слова: объем тела вращения; цилиндрические оболочки; кратный и определенный интегралы.
Актуальность исследования заключается в насущной необходимости определения объемов тел вращения плоских фигур вокруг оси ординат. Целью исследования является изучение наиболее экономичного метода вычисления объемов.
Пусть ![]() – область, ограниченная сверху графиком функции
– область, ограниченная сверху графиком функции ![]() , сни-зу осью
, сни-зу осью ![]() , с двух сторон прямыми
, с двух сторон прямыми ![]() ,
, ![]() . Требуется определить объем
. Требуется определить объем ![]() тела вращения
тела вращения ![]() , получаемого вращением области
, получаемого вращением области ![]() вокруг оси
вокруг оси ![]() .
.
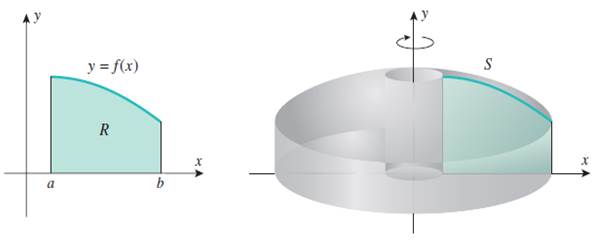
Рисунок 1. Область R и тело вращения этой области вокруг оси ![]()
Объем тела, получающегося при вращении области R вокруг оси ![]() , вычисляется с помощью определенного интеграла [1-3]:
, вычисляется с помощью определенного интеграла [1-3]:

Объем тела, получающегося при вращении области R вокруг оси ![]() , вычисляется с помощью кратных интегралов [1-3] и определенного интеграла [4]:
, вычисляется с помощью кратных интегралов [1-3] и определенного интеграла [4]:

Цилиндрическая оболочка – это твердое тело, окруженное двумя концентрическими правильными круглыми цилиндрами.

Рисунок 2. Цилиндрическая оболочка
Как известно, объем цилиндрической оболочки с внутренним радиусом ![]() и внешним радиусом
и внешним радиусом ![]() и высотой
и высотой ![]() вычисляется так
вычисляется так
![]()
![]()
Основная идея определения указанного объема состоит в разделении отрезка ![]() на
на ![]() внутренних интервалов. Тогда область
внутренних интервалов. Тогда область ![]() делится соответственно на следующие
делится соответственно на следующие ![]() полос:
полос: ![]() ,
, ![]() , …,
, …, ![]() . При вращении области
. При вращении области ![]() вокруг оси
вокруг оси ![]() эти полосы образуют трубообразные тела
эти полосы образуют трубообразные тела ![]() ,
, ![]() , …,
, …, ![]() , лежащие одна внутри другой и все они вместе образуют тело
, лежащие одна внутри другой и все они вместе образуют тело ![]() .
.
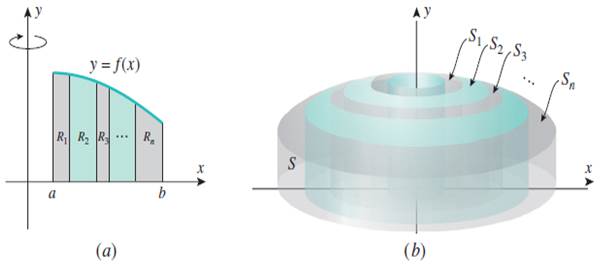
Рисунок 3. Тела вращений полос области ![]() вокруг оси
вокруг оси ![]()
Объем тела вращения ![]() определяется сложением объемов трубообразных твердых тел
определяется сложением объемов трубообразных твердых тел ![]() ,
, ![]() , …,
, …, ![]() :
:
![]() Обычно внешние поверхности этих трубообразных тел
Обычно внешние поверхности этих трубообразных тел ![]()
![]() сильно изогнуты и поэтому не существуют простых формул для определения объемов
сильно изогнуты и поэтому не существуют простых формул для определения объемов ![]()
![]() . Если же полосы достаточно тонкие, то можно аппроксимировать каждую полосу прямоугольником. При вращении каждой полосы вокруг оси
. Если же полосы достаточно тонкие, то можно аппроксимировать каждую полосу прямоугольником. При вращении каждой полосы вокруг оси ![]() образуется цилиндрическая оболочка и ее объем приблизительно равен объему трубы, образованной прямоугольником.
образуется цилиндрическая оболочка и ее объем приблизительно равен объему трубы, образованной прямоугольником.
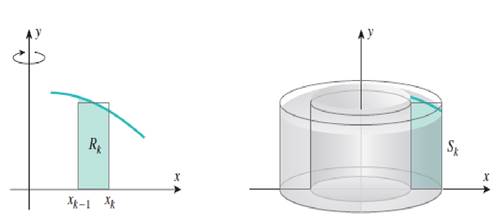
Рисунок 4. Аппроксимация полосы области ![]() прямоугольником
прямоугольником
Складывая объемы цилиндрических оболочек определяют сумму Римана, которая аппроксимирует искомый объем ![]() , и вычисляя предел сумм Римана получают интеграл, который точно вычисляет значение объема
, и вычисляя предел сумм Римана получают интеграл, который точно вычисляет значение объема ![]() . Для осуществления данной идеи считают, что
. Для осуществления данной идеи считают, что ![]() -тая полоса тянется от точки
-тая полоса тянется от точки ![]() до точки
до точки ![]() , а ширина такой полосы равна
, а ширина такой полосы равна ![]() . Пусть
. Пусть ![]() - средняя точка отрезка
- средняя точка отрезка ![]() . При вращении прямоугольника с высотой
. При вращении прямоугольника с высотой ![]() вокруг оси
вокруг оси ![]() образуется цилиндрическая оболочка со средним радиусом
образуется цилиндрическая оболочка со средним радиусом ![]() , с толщиной
, с толщиной ![]() и высотой
и высотой ![]() .
.
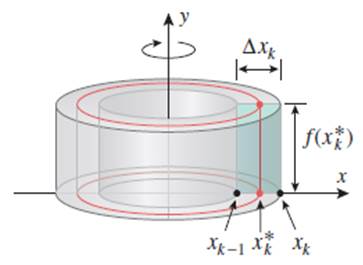
Рисунок 5. Образование цилиндрической оболочки
Объем ![]() частной цилиндрической оболочки определяется формулой:
частной цилиндрической оболочки определяется формулой:
![]()
Сложив объемы всех ![]() цилиндрических оболочек, получим следующую сумму Римана, которая аппроксимирует объем
цилиндрических оболочек, получим следующую сумму Римана, которая аппроксимирует объем ![]() тела вращения:
тела вращения:
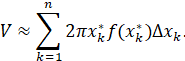
Если перейти к пределу при неограниченном увеличении числа интервалов ![]() и уменьшении ширины всех интервалов до нуля, то получится определенный интеграл:
и уменьшении ширины всех интервалов до нуля, то получится определенный интеграл:

Заключение. Объем ![]() тела, которое получается при вращении области
тела, которое получается при вращении области ![]() вокруг оси
вокруг оси ![]() , вычисляется с помощью определенного интеграла (1) [4, с. 434].
, вычисляется с помощью определенного интеграла (1) [4, с. 434].
Далее, на примерах 1-5 показывается экономичность вычисления объемов тел вращения вокруг оси ординат помощью формулы (1).
Пример 1. С помощью цилиндрических оболочков определите объем тела, которое получается при вращении области, ограниченной заданными прямыми ![]() ,
, ![]() ,
, ![]() , вокруг оси
, вокруг оси ![]() .
.
Решение. Объем тела вращения вычисляется формулой (1):
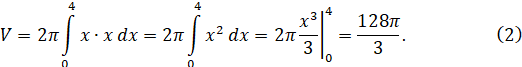

Рисунок 6. Треугольная область для вращения вокруг оси ![]()
Проверка. ![]() , где
, где ![]() – объем цилиндра с радиусом
– объем цилиндра с радиусом ![]() круга основания и высотой
круга основания и высотой ![]() ,
, ![]() – объем конуса, находящегося внутри данного цилиндра, с радиусом
– объем конуса, находящегося внутри данного цилиндра, с радиусом ![]() круга основания и высотой
круга основания и высотой ![]() . Тогда объем цилиндра
. Тогда объем цилиндра
![]()
и объем конуса
![]()
или

Поэтому искомый объем тела вращения
![]()
т.е. результат (2), найденный с помощью цилиндрических оболочек, верен.
Пример 2. Определите с помощью цилиндрических оболочек объем тела вращения, получающегося вращением плоской области, ограниченной прямыми ![]() ,
, ![]() 0,
0, ![]() ,
, ![]() , вокруг оси
, вокруг оси ![]() .
.
Решение. Объем такого тела вращения можно вычислить формулой (1):

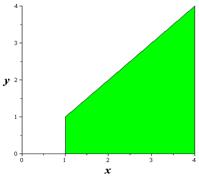
Рисунок 7. Трапециодальная область для вращения вокруг оси ![]()
Проверка. ![]() , где
, где ![]() – объем цилиндра с радиусом круга основания и высотой
– объем цилиндра с радиусом круга основания и высотой ![]() ,
, ![]() – объем усеченного конуса внутри цилиндра с радиусами кругов основания
– объем усеченного конуса внутри цилиндра с радиусами кругов основания ![]() ,
, ![]() и высотой
и высотой![]() ,
, ![]() – объем внутреннего цилиндра с радиусом основания
– объем внутреннего цилиндра с радиусом основания ![]() и высотой
и высотой ![]() . Следовательно, объем цилиндра
. Следовательно, объем цилиндра
![]()
объем усеченного конуса
![]()
или
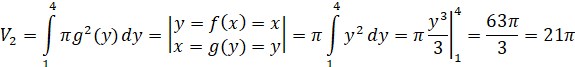
и объем внутреннего цилиндра
![]()
Поэтому объем тела вращения
![]()
то есть результат (3), найденный с помощью цилиндрических оболочек, верен.
Пример 3. Определите с помощью цилиндрических оболочек объем тела вращения области, ограниченной кривой ![]() и прямыми
и прямыми ![]() ,
, ![]() (см. рис. 8а).
(см. рис. 8а).
Решение. Объем тела вращения вычисляется формулой (1):

Проверка. ![]() , где
, где ![]() – объем цилиндра с радиусом
– объем цилиндра с радиусом ![]() и высотой
и высотой ![]() ,
, ![]() – объем внутреннего конусообразного тела с радиусом
– объем внутреннего конусообразного тела с радиусом ![]() круга основания сол и высотой
круга основания сол и высотой ![]() . Следовательно, объем цилиндра
. Следовательно, объем цилиндра
![]()
и объем конусообразного тела

Поэтому объем тела вращения
![]()
то есть результат (4), найденный с помощью цилиндрических оболочек, верен.
Пример 4. Определите с помощью цилиндрических оболочек объем тела вращения области, ограниченной кривой ![]() и прямыми
и прямыми ![]() ,
, ![]() , во-круг оси
, во-круг оси ![]() .
.
Решение. Объем тела вращения вычисляется формулой (2):

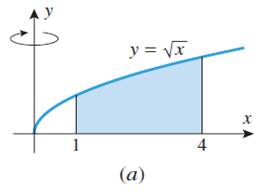

Рисунок 8. Параболическая область для вращения вокруг оси ![]()
Проверка. ![]() , где
, где ![]() – объем цилиндра с радиусом
– объем цилиндра с радиусом ![]() круга основания и высотой
круга основания и высотой ![]() ,
, ![]() – объем внутреннего конусообразного тела с радиусом
– объем внутреннего конусообразного тела с радиусом ![]() круга основания и высотой
круга основания и высотой ![]() ,
, ![]() – объем внутреннего цилиндра с радиусом
– объем внутреннего цилиндра с радиусом ![]() круга основания и высотой
круга основания и высотой ![]() . Объем цилиндра
. Объем цилиндра
![]() ,
,
объем усеченного конусообразного тела

и объем внутреннего цилиндра
![]()
Поэтому объем тела вращения
![]()
то есть результат (5), найденный с помощью цилиндрических оболочек, верен.
Пример 5. Определите с помощью цилиндрических оболочек объем тела вращения фигуры, ограниченной прямой ![]() и кривой
и кривой ![]() , вокруг оси
, вокруг оси ![]() .
.
Решение. Объем тела вращения вычислятся формулой (1):
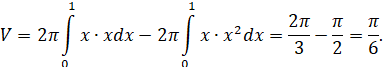

Рисунок 9. Лепестковая область для вращения вокруг оси ![]()





