ТУННЕЛЬНЫЙ ЭФФЕКТ В ЯВЛЕНИИ ПОЛНОГО ВНУТРЕННЕГО ОТРАЖЕНИЯ СВЕТА
Секция: 3. Физические науки

XIII Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: естественные и медицинские науки»
ТУННЕЛЬНЫЙ ЭФФЕКТ В ЯВЛЕНИИ ПОЛНОГО ВНУТРЕННЕГО ОТРАЖЕНИЯ СВЕТА
Туннельный эффект — это преодоление микрочастицей потенциального барьера в случае, когда её полная энергия меньше высоты барьера. Раньше полагали, что туннельный эффект это явление исключительно квантовой природы, невозможное в классической механике и даже полностью противоречащее ей. Классический шарик никогда не перекатится через горку, если его кинетическая энергия меньше потенциальной энергии шарика на вершине горки. Причиной туннельного эффекта для микрочастиц по гипотезе де Бройля является волновая природа микрочастиц. Длина волны де Бройля равна отношению импульса микрочастицы к постоянной Планка:
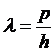 .
.
Решение волнового уравнения Шредингера для падения волн де Бройля на потенциальный барьер приводит к выводу, что волны частично проникают сквозь барьер. Коэффициент прозрачности барьера, равный доле частиц, проникших через барьер, определяется формулой:
![]() ,
,
где:  — волновой вектор.
— волновой вектор.
Как видно, коэффициент прозрачности отличен от нуля, если ширина барьера меньше длины волны.
Итак, причиной туннельного эффекта в микромире является волновая природа микрочастиц. Поэтому можно предполагать, что подобное явление может наблюдаться для волн другой природы. Тем более что основное уравнение квантовой механики — уравнение Шредингера, получено преобразованием волнового уравнения, справедливого для волн любой природы, введением вместо длины волны импульса микрочастицы.
Действительно, для световых волн туннельный эффект наблюдается. Он проявляется в проникновении световой волны через границу раздела со средой в условиях, когда с точки зрения геометрической оптики происходит полное внутреннее отражение. Глубина проникновения порядка длины световой волны [1; 2]. Туннельный эффект наблюдается даже для механических волн, например, для волн на поверхности воды [3].
Целью данной работы является разработка макета лабораторной установки «Исследование туннельного эффекта». Экспериментальное исследование явления туннельного эффекта было проведено на примере световых волн. Для этого применялась установка, состоящая из лазера и двух стеклянных призм (рисунок 1). Призмы прижимались друг к другу с помощью винтового зажима. Интенсивность излучения измерялась с помощью кремниевого фотоэлемента по величине фотоЭДС.
Свет лазера под разными углами падает в центр первой стеклянной призмы. Если угол падения луча лазера превысит предельный угол полного внутреннего отражения ![]() , то преломленного луча исчезает. Здесь n — показатель преломления стекла призм. Но если подставить и прижать вторую призму с зазором меньше чем длина волны, то луч свет проникает через зазор. В этом заключается явление туннельного эффекта для световых волн.
, то преломленного луча исчезает. Здесь n — показатель преломления стекла призм. Но если подставить и прижать вторую призму с зазором меньше чем длина волны, то луч свет проникает через зазор. В этом заключается явление туннельного эффекта для световых волн.

Рисунок 1. Схема установки
При отсутствии нижней призмы в пределах углов падения от нуля до угла полного внутреннего отражения (43о), направление преломленного луча подчиняется закону преломления света. При превышении угла падения луча лазера свыше 43 градусов преломленный луч отсутствует.
При обеих сжатых призмах направление распространения луча, проникшего через зазор в интервале углов падения от нуля до 90о градусов, совпадает с направлением распространения луча лазера.

Рисунок 2. Зависимость интенсивности излучения от угла падения луча лазера
Интенсивность прямого луча, прошедшего через зазор в интервале от нуля до 43о примерно постоянна. Точно также как было бы при отсутствии второй призмы (рисунок 2). При превышении угла падения угла полного внутреннего отражения интенсивность монотонно убывает до нуля. Причем в зоне перехода, когда прямой луч превращается в луч, прошедший вследствие туннельного эффекта, интенсивность изменяется плавно. Изменяется только распределение яркости по сечению луча от центра к краям.
Самым важным в данной работе является исследование зависимости интенсивности проникающего при полном внутреннем отражении луча от величины зазора. Достаточно чуть-чуть ослабить зажимы, прижимающие призмы друг к другу, как проникающий луч исчезает. Величину зазора d будем считать пропорциональной силе F, с который оттягивали нижнюю призму и, соответственно, деформации пружины. Согласно уравнению коэффициента прозрачности спад интенсивности должен происходить по экспоненциальному закону. Это более четко проявляется, если построить график зависимости логарифма интенсивности от деформации пружины (рисунок 3). Как видно, зависимость, с точностью до погрешности опыта, подчиняется линейной зависимости.

Рисунок 3. Зависимость логарифма интенсивности от нажатия
пружины
Проделав данную работу, мы обнаружили прохождение световой волны через воздушный зазор между призмами при явлении полного внутреннего отражения, что является проявлением туннельного эффекта. Установлена экспоненциальная зависимость интенсивности проникающего через зазор луча от усилия пружины, раздвигающей зазор. В лабораторной установке следует воздушный зазор выполнить в форме клина с углом ![]() , где h — толщина пленки, устанавливаемая на краю между призмами. При этом луч лазера перемещать вдоль зазора от места угла клина.
, где h — толщина пленки, устанавливаемая на краю между призмами. При этом луч лазера перемещать вдоль зазора от места угла клина.
Список литературы:
1. Ландсберг Г.С. Оптика — М.: Наука, 1979 — 486 с.
2. Крауфорд Ф. Волны — М.: Наука,1975 — 308 с.
3. Поль Р.В. Механика, акустика и учение о теплоте — М.:Наука,1971 — 271 с.





