ПРИМЕНЕНИЕ АЛГЕБРАИЧЕСКИХ МЕТОДОВ ДЛЯ ДОКАЗАТЕЛЬСТВА ГЕОМЕТРИЧЕСКИХ ТЕОРЕМ

Аннотация. Наша цель в данной статье - продемонстрировать доказательство геометрических теорем, используя алгебраические методы. Введем, декартовы координаты на евклидовой плоскости. Затем мы можем написать полиномиальные уравнения, связывающие координаты набора точек указаны в гипотезах и выводах этих теорем. При работе с большими системы уравнений, имеющие алгебраическую структуру для представления геометрических теорем, позволяет использование технологий для эффективной проверки выводов теорем. Чтобы использовать технологии, однако у нас должны быть соответствующие входные данные, и мы должны знать, как интерпретировать результаты. Компьютерная программа может быстро выполнять алгоритмы, но не может осуществлять планирование. Если мы не знаем, какой результат нам нужен, мы не узнаем, доказана ли теорема.

От геометрических теорем к полиномиальным уравнениям

Свойства геометрических фигур, таких как линии, углы, многоугольники и окружности. не изменяется при перемещении и вращении в евклидовой плоскости, поэтому, когда мы вводим Декартовы координаты, мы можем расположить объект нашей теоремы в любом удобном месте. Координаты одних точек будут произвольными, а другие будут зависеть от произвольные. Обычной практикой является использование переменных u_i для представления произвольных значений. и x_i для представления координат, определяемых произвольными.

Следующее предложение перечисляет геометрические утверждения, которые мы будем использовать в примерах.

Предложение. Пусть A, B, C, D — различные точки плоскости. Тогда каждое утверждение может быть выражена одним или несколькими полиномиальными уравнениями.

(i) A, B, C коллинеарные.

(ii) AB перпендикулярна CD.

(iii) Расстояние от A до B равно расстоянию от C до D: AB = CD

(iv) C является серединой 

Доказательство. Пусть A = (a₁, a₂), B = (b₁, b₂), C = (c₁, c₂) и D = (d₁, d₂) — различные точки в самолет.

(і) Точки A, B и C лежат на одной прямой, если наклоны и  равны. С использованием формула наклона, мы имеем

Отсюда можно получить полиномиальное уравнение

p₁ = (a₂ − b₂)(b₁ − c₁) − (a₁ − b₁)(b₂ − c₂) = 0.

(ii) Чтобы показать, что  ⊥, мы выражаем  как вектор (b₁ − a₁, b₂ − a₂), а  как вектор (d₁ − c₁, d₂ − c₂). Тогда  ⊥  означает, что векторы ортогональны.  Другими словами, скалярное произведение равно нулю. Итак, у нас есть

(b₁ − a₁, b₂ − a₂) · (d₁ − c₁, d₂ − c₂) = 0

что дает полиномиальное уравнение

p₂ = (b₁ − a₁)(d₁ − c₁) + (b₂ − a₂)(d₂ − c₂) = 0.

(iii) Чтобы показать AB = CD, мы используем формулу расстояния, чтобы показать AB² = CD².

АВ² = (b₁ - а₁)² + (b₂ - а₂)²

CD² = (d₁ − c₁)² + (d₂ - с₂₎²

Теперь AB² = CD² дает полиномиальное уравнение

р₃ = (b₁ - а₁)² + (b₂ - а₂)² - (d₁ - с₁)² - (d₂ - с₂)² = 0

(iv) Если C является серединой AB, то A, B и C коллинеарны и AC = BC, поэтому мы имеем полиномиальные уравнения из утверждений (i) и (iii).

Другие общие геометрические утверждения, такие как две прямые параллельны, точка находится на окружность, прямая касается окружности, а прямая делит угол пополам, также могут быть выражены как полиномиальные уравнения.

Пример. Ортоцентр треугольника.

Средний геометрический системе ортоцентр треугольника определяется как точка, в которой пересекаются три высоты треугольника. Уделяется внимание кажущееся противоречивым представление о том, что центр треугольника на самом деле может находиться за пределами треугольник или, в случае прямоугольного треугольника, быть одной из вершин, но мысль о том, что такая точка параллелизма существует, считается данностью. Здесь мы докажем, что все три высоты треугольника совпадают.

Теорема. Пусть ∆ABC — треугольник на плоскости. Затем строки, содержащие высоты треугольника сходятся в одной точке, называемой ортоцентром треугольника.

Высота из вершины A — это отрезок прямой из A, пересекающий прямую, содержащую противоположная сторона  под прямым углом. Как показано на рисунке ниже, мы будем называть это точки встречи D и обратите внимание, что сторона  была расширена, чтобы точка пересечения могла быть идентифицированы. Высота от вершины B - это отрезок прямой из B, пересекающий прямую содержащий противоположную сторону  под прямым углом. На рисунке ниже это пересечение точка помечена E. Высота от вершины C — это отрезок линии от C, пересекающий противоположная сторона  под прямым углом. Как показано ниже, сторона  расширена, а точка пересечения помечена буквой F

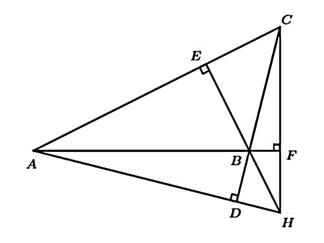
Рисунок 1. ∆ABC с высотами

Мы снова поместим A в начало координат и выровняем AB по горизонтальной координате ось, поэтому A = (0, 0) и B = (u₁, 0). Пусть C = (u₂, u₃). Координаты подножия р высота от каждой вершины до линии, содержащей противоположную сторону каждой стороны треугольника полностью определяются вершинами. Имеем D = (x₁, x₂), E = (x₃, x₄), F = (х₅, х₆). Координаты ортоцентра также полностью определены, поэтому мы напишите Н = (х₇, х₈). Теперь, мы можем получить полиномиальные уравнения из гипотезы:

B, D, C коллинеарно: 

производит

h₁ = x₂(u₂ − u₁) − u₃(x₁ − u₁) = 0.

Выражая отрезки в виде векторов, имеем

AD ⊥ : AD · BC = (x1, x2) · (u2 − u1, u3) = 0

который производит

h₂ = x₂u₃ + x₁(u₂ − u₁) = 0.

Так же,

A, E, C коллинеарны: h₃ = x₄u₂ − x₃u₃ = 0

 ⊥  : h₄ = x₄u₃ + u₂(x₃ − u₁) = 0

A, B, F коллинеарны: h₅ = x₆ = 0

 ⊥  : h₆ = u₂ − x₅ = 0

Теперь мы идентифицируем H как точку, где пересекаются две высоты,  и , что дает еще два гипотетических полинома:

A, D, H коллинеарны: h₇ = x₂x₇ − x₁x₈ = 0

B, E, H коллинеарны: h₈ = x₄(x₇ − u₁) − x₈(x₃ − u₁) = 0

Вывод, H также на высоте CF переводится

C, F, H коллинеарны: g = (x₆ − u₃)(x₇ − u₂) − (x₅ − u₂)(x₈ − u₃) = 0

Приведенный базис Гребнера для идеала

(h₁, h₂, h₃, h₄, h₅, h₆, h₇, h₈, 1 – yg) ⊂ (u₁, u₂, u₃)[x₁, . . . , х₈, у]

представленный «Сейдж» с использованием порядка lex, соответствует, как и хотелось, поэтому мы заключаем, что g обращается в нуль на V (h₁, h₂, h₂, h₄, h₅, h₆, h₇, h₈), что подтверждает вывод о том, что точка H находится на высоте .

Мы описали, как выразить геометрическую теорему в виде системы многочленов уравнения, так что компьютер может быть использован для проверки теоремы. Единственная часть доказательства, которая требует человеческого рассуждения, - это вывод система полиномиальных уравнений.