Практическое применение теоремы Холла в профессиональной сфере, её алгоритмизация и программирование
Секция: Технические науки

XL Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Практическое применение теоремы Холла в профессиональной сфере, её алгоритмизация и программирование
Аннотация. Задумывались ли вы когда-нибудь над тем, что графы имеют широкое распространение в повседневной жизни? Без них реализация многих привычных нам вещей была бы сложна или даже невозможна. В рамках данной работы нам удалось доказать это, а также автоматизировать на примере практического применения одной из теорем, входящих в теорию графов, а именно, теоремы Холла.
Ключевые слова: граф, двудольный граф, теорема Холла, алгоритмизация, блок-схемы, неориентированный граф, практическое применение, теорема Форда-Фалкерсона, метод математической индукции, автоматизация.
В современном мире каждый человек что-то слышал про «граф». Но не все могут представить, как обширно его применение во всех областях жизнедеятельности. Теорема Холла, рассматриваемая в данной статье, также нашла своё отражение в различных сферах деятельности. При изучении наибольший интерес вызвала профессиональная сфера, где применение графов неочевидно, а также возможность алгоритмизации и автоматизации теоремы.
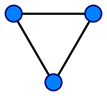
Граф — совокупность точек и линий, проведенных между точками [1].
|
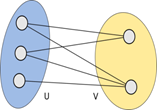
Неориентированный граф G – упорядоченная пара G:=(V,E), где V – непустое множество вершин или узлов, Е – множество пар неупорядоченных вершин (рёбра). Один из видов графов, двудольный, рассматривается и в исследуемой теореме Холла [2]. |
Рисунок 1. Неориентированный граф |
|
|
Рисунок 2. Двудольный граф |
Двудольный граф – это граф, множество вершин которого можно разбить на две части так, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует рёбер между вершинами одной и той же части [4]. |
|
Доказанная в 1935 году Филиппом Холлом теорема также имеет непосредственное отношение к теории графов и её практическому применению. В общественности она наиболее известна как «Теорема о свадьбах». Официальная формулировка теоремы Холла: Необходимое и достаточное условие состоит в том, чтобы любое множество из k объектов одного множества в совокупности «предпочитает» по меньшей мере k объектов из другого множества, 1 ≤ k ≤ n.
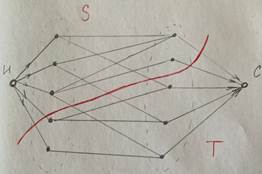
Доказательство можно проводить двумя методами: метод математической индукции, с помощью теоремы Форда-Фалкерсона. Рассмотрим второй вариант. Теорема Форда-Фалкерсона: мощность максимального потока сети равна минимальной пропускной способности её разрезов (линии, делящей граф на две несвязные части). Следовательно, максимальный поток равен количеству вершин, входящих в первую долю. Это означает выполнение условия теоремы Холла [3].
|
|
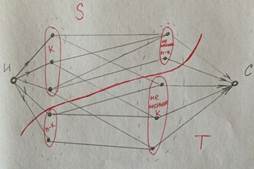
Рисунок 4. Определение пропускной способности разреза |
С помощью разреза каждая доля двудольного графа была разделена на 2 части. Известно, что в первой доле содержалось n вершин. Предположим, что в той части доли, которая относится к стороне разреза S, содержится k вершин (k<n). Тогда в части, относящейся к стороне разреза T, n-k вершин (рисунок 4). Исходя из условия теоремы Холла, во второй доле, относящейся к стороне разреза T, не меньше k вершин. Соответственно, в части, относящейся к стороне разреза S, не меньше n-k вершин. Следовательно, суммарная пропускная способность разреза будет не меньше n.
С практической точки зрения теорема Холла нашла широкое применение в разных сферах деятельности человека: процессы, события, имеющие отношение к каким-либо распределительным задачам. Подробнее рассмотрим применение данной теоремы в профессиональной сфере:
1. приём сотрудников на работу в организацию. Неотъемлемая часть поиска работы - резюме. Со стороны работодателя необходимо отсортировать и просмотреть в зависимости от направленности и желания потенциального сотрудника каждое из резюме;
2. распределение отпусков среди отдела какой-либо организации. В соответствии с законом каждый сотрудник должен ежегодно уходить в отпуск на определённый период. Но при этом компания не должна переставать функционировать, то есть постоянно должен работать каждый из отделов;
3. атака на компьютерные системы. Для наибольшего охвата каждый хакер (член группы) должен специализироваться и отвечать за конкретную область компьютерной системы.
Рассмотрим конкретную ситуацию и варианты исходов для каждой из поставленных выше задач. Пусть n в каждой из задач – это количество человек, m – это:
a. количество должностей;
b. количество месяцев для отпуска;
c. количество областей воздействия.
1. Рассмотрим неблагоприятный исход. Для всяких m < n:
|
Рисунок 5. Реализация ситуации 1 |
2. Может быть и такая ситуация, что m = n, но теорема Холла всё равно не выполнится:
|
Рисунок 6. Реализация ситуации 2 |
3. Рассмотрим относительно благоприятную ситуацию, когда m > n:
|
Рисунок 7. Реализация ситуации 3 |
4. Рассмотрим благоприятный исход, когда n = m и выполняется теорема Холла:
|
Рисунок 8. Реализация ситуации 4 |

Рисунок 9. Алгоритмизация теоремы Холла (пример 1)
На рисунке 9 все рассмотренные ситуации преобразованы в общую блок – схему для примера №1, то есть, произведена алгоритмизация.
Исходя из проведенных исследований, помимо очевидных областей применения, таких как транспортное сообщение и сетевые коммуникации, выяснено, что графы, а именно двудольные, применяются в трудовой сфере. Особое внимание было уделено теореме Холла, её алгоритмизации и автоматизации. В наше время автоматизация различных процессов играет немаловажную роль, позволяя упростить пользователю работу, сократить временные затраты. Её реализация возможна на различных языках программирования, наиболее популярные из которых – это С, С++, C#, Python, Java. Выбор какого-либо из них зависит от задачи, которую необходимо решить. Для автоматизации теоремы Холла подходит язык программирования Python.
На рисунках 9 и 10 приведены результаты работы программы в различных ситуациях (корректная и некорректная). Очевидно, что при невнимательности или невозможности подобрать наилучший вариант решения задачи, программа не выдаёт итогового распределения, что уберегает пользователя от ошибки.
|
Рисунок 10. Результат выполнения программы при корректных данных |
Рисунок 11. Результат выполнения программы при некорректных данных |
На рисунках 12 – 15 представлен код разработанной программы, включающий в себя рассмотрение различных ситуаций и принятие решений в зависимости от имеющегося набора информации.
|
Рисунок 12. Код программы (часть 1) |
Рисунок 13. Код программы (часть 2) |
|
|
|
Очевидно, что теорема Холла, её алгоритмизация и автоматизация способны существенно упростить пользователю процесс распределения. Созданная программа может применяться в различных областях деятельности, выполняя ряд задач вместо человека, что поспособствует повышению производительности и сокращению затрат человеческих ресурсов на задачи распределения.