ТЕОРЕМА ЕДИНСТВЕННОСТИ РЕШЕНИЯ БЕСКОНЕЧНОЙ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

UNITY THEOREM FOR SOLUTIONS OF AN INFINITE SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS

Madina Gazdieva

Student Ingush State University, Russia, Magas

Ismail Tankiev

Scientific adviser,  Candidate of physical and mathematical sciences, Head of the Department of Mathematical Analysis, Professor,

Ingush State University,  Russia, Magas

Аннотация. В данной статье рассматривается теорема единственности  решения бесконечной системы обыкновенных дифференциальных уравнений, а также её доказательство.

Abstract. In this article, we consider the uniqueness theorem for the solution of an infinite system of ordinary differential equations, as well as its proof.

Ключевые слова: бесконечная система ОДУ, теорема Тихонова, единственность решения, условие Липшица.

Keywords: infinite system of ODE, Tikhonov's theorem, uniqueness of a solution, Lipschitz condition.

Первой по времени теоремой существования и единственности решения бесконечной системы нелинейных дифференциальных уравнений

была теорема, принадлежащая А. Н. Тихонову [1].

Относительно правых частей системы (1) предполагается, что:

1) функции  определены при  в области D:

2) функции  непрерывны по совокупности переменных  при фиксированном 

3) при фиксированных  функции  измеримы по 

4) при произвольном выборе переменных  из области D функции  удовлетворяют условиям

для всех  где  функция положительная, суммируемая в отрезке: 

5) интеграл Лебега от функции  ограничен

Итак, рассмотрим бесконечную систему (1).

Теорема. (А. Н. Тихонов). Если выполняются условия 1)–5), то существует, по крайней мере, одна система решений системы уравнений (1), удовлетворяющая начальным условиям

где  произвольная система начальных значений.    

Установим условия однозначности решения задачи (1)(3). Мы скажем, что система функций  удовлетворяет условиям Липшица относительно переменных  …, если

Теорема (А. Н. Тихонов). Пусть дана бесконечная система дифференциальных уравнений, правые части которой  удовлетворяют условия Липшица (4), ряды

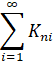сходятся и равноограничены, т.е.

Тогда существует одна и только одна система решений  удовлетворяющая начальным условиям (3), для которой выполнено условие

(равномерно ограничена).

Доказательство: Пусть  и  две системы решений уравнений (1), удовлетворяющие одним и тем же начальным условиям (3)

и еще условиям

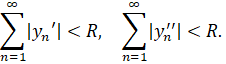
Тогда из системы уравнений (1) имеем

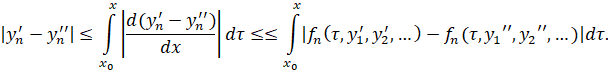
В силу (4) получим

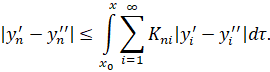
Отсюда следует, что

На основании (5) получим неравенство

Принимая во внимание условие (6), получим

Отсюда следует, что положительная возрастающая последовательность равномерно ограничена и производная каждой  по , как легко видеть, меньше  Следовательно, эта последовательность сходится к непрерывной положительной функции Y(x), для которой выполняется неравенство

Это неравенство может удовлетворяться только при  ибо предположение о том, что ее максимум на отрезке  равен числу  приводит к противоречию:

Следовательно, имеют место тождества

которые доказывают теорему [2-5].