РАСЧЁТ НАГРЕВА СТЕНКИ РЕЗЕРВУАРА В ПРОГРАММЕ Elcut
Журнал: Научный журнал «Студенческий форум» выпуск №19(242)
Рубрика: Технические науки

Научный журнал «Студенческий форум» выпуск №19(242)
РАСЧЁТ НАГРЕВА СТЕНКИ РЕЗЕРВУАРА В ПРОГРАММЕ Elcut
Для расчета Elcut использует метод конечных элементов [1 с.103]. В качестве единственного типа конечных элементов разработчиками был выбран линейный треугольник. Использование метода конечных элементов позволяет практически снять ограничения на сложность расчетной области, нелинейность свойств материалов.
В программе Elcut 6.2 была создана геометрическая модель системы, а также заданы условия задачи представленные на рисунке 1 и 2 соответственно.

Рисунок 1. Геометрическая модель системы «примыкающий индуктор – плоская загрузка»
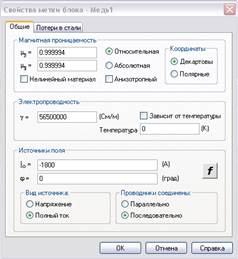
Рисунок 2. Окно задания электромагнитных свойств метки блока «Медь»
На этапе моделирования рассмотрен нагрев пластины толщиной 10 мм. Толщина воздушного зазора между примыкающим индуктором и загрузкой – 5 мм. Картина распределения плотности тока представлена на рисунке 3. Черными линиями показаны линии магнитного поля, цветная картина – распределение плотности тока. Наибольшее значение плотности тока – на поверхности в центре загрузки j = 4,5·106 ![]() а к полюсам магнитопровода и по толщине материала она уменьшается.
а к полюсам магнитопровода и по толщине материала она уменьшается.
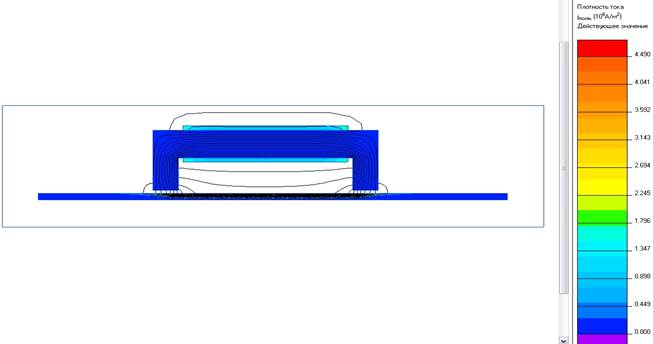
Рисунок 3. Картина распределения плотности тока при одностороннем нагреве плоской загрузки
График распределения плотности тока по толщине загрузки представлен на рисунке 4. Из графика видно, что на нижней границе загрузки плотность тока равна 0, т.е. в воздушном зазоре и загрузке выделяется 100 % активной мощности электромагнитного поля, преобразованной в теплоту.
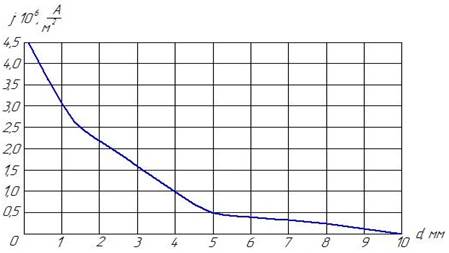
Рисунок 4. График распределения плотности тока по толщине загрузки
Проведено исследование распределения основных параметров электромагнитного поля под индуктором по длине загрузки (на глубине 5 мм). К основным параметрам электромагнитного поля относятся напряженность, индукция, плотность тока и тепловыделение.
Наибольшие значения параметры электромагнитного поля имеют в центре загрузки, а к полюсам магнитопровода их значения уменьшаются до 0. Использование магнитопровода позволяет сконцентрировать основную часть магнитного потока под индуктором.
Далее был произведен расчет задачи нестационарной теплопередачи.
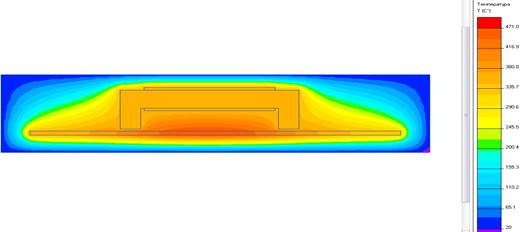
Рисунок 5. Картина распределения температуры по объему загрузки при одностороннем нагреве
Из анализа картины распределения температуры по объему загрузки, приведенной на рисунке 5, следует, что наибольшая температура в центре загрузки, а к полюсам магнитопровода она уменьшается. Наибольшее значение температуры составляет 470 0С, наименьшее – 399 0С. Разница температур между центром загрузки и полюсами магнитопровода составляет 71 0С, что говорит о неравномерности нагрева и концентрации основных источников тепла под обмоткой.
Вывод: при моделировании нагрева одним индуктором наибольшие значения основных параметров электромагнитного и теплового полей находятся в центре загрузки под магнитопроводом, а к полюсам магнитопровода они уменьшаются.
Разность температур при нагреве одним индуктором составляет 71 0С, что говорит о неравномерном нагреве. Применение нескольких индукторов смещенных друг от друга на определенное расстояние должно позволить добиться равномерного нагрева.

