ИССЛЕДОВАНИЕ ВЗАИМОСВЯЗИ МАКСИМАЛЬНЫХ ПРОГИБОВ И СОБСТВЕННЫХ ЧАСТОТ ПОПЕРЕЧНЫХ КОЛЕБАНИЙ МНОГОСЛОЙНЫХ ТРЕУГОЛЬНЫХ ПЛАСТИН С ЖЕСТКИМ ОПИРАНИЕМ ПО КОНТУРУ

Работа многослойных изотропных пластин на податливых механических связях является актуальной проблемой. Пластинки разнообразной формы в настоящее время являются распространенными строительными конструктивными элементами, которые подвержены воздействию не только статических, но и динамически нагрузок.

В данной работе рассматривается взаимосвязь граничных условий, произведения частот собственных поперечных колебаний пластины ω и максимального прогиба W0 при действии равномерно распределённой нагрузки q.

Численные исследования составных двухслойных пластин на податливых связях проводились методом конечных элементов. В ходе численных исследований определение прогибов и частот колебаний проводилось в программном комплексе «ЛИРА САПР». В качестве модели исследования была выбрана треугольная двухслойная составная пластина. Каждый слой был разбит сеткой 40×40 на конечные элементы (КЭ); таким образом, размер каждого конечного элемента составил 100×100 мм.

Толщина пластин задавалась различной: толщина нижней пластины принята постоянной 5 мм, толщина верхней принималась равной 3…15 мм. Пластины связаны между собой поперечными связями (препятствующими сближению и отдалению слоёв) и связями сдвига. При исследованиях жесткость связей принята постоянной и составляла ЕА_пс = 512000 Н для поперечных связей, ЕА_сс=10000 Н для связей сдвига. Плотность материала слоёв принята ρ = 740 кг/м³. Все исследования производились в предположении упругой стадии работы материала слоев, поперечных связей и связей сдвига.

Критерием точности во всех исследованиях служил коэффициент K, который определялся из (1):

Этот коэффициент для прямоугольных пластин с различными опираниями по контуру различны.

Пластины загружались равномерно распределенной нагрузкой q = 1 кН/м2, которая прикладывалась к верхнему слою составной пластины. Для нахождения частот собственных колебаний в узлы конечных элементов прикладывались сосредоточенные массы от собственного веса слоев в зависимости от грузовой площади узла.

Частоты собственных колебаний и максимальный прогиб двухслойной пластины, полученные при расчёте в программном комплексе «ЛИРА САПР» приведены в таблице 1. По данным таблицы 1 построены графики изменения максимальных прогибов и частот колебаний в зависимости от отношения толщин t₂/t₁, представленные на рисунке 1.

Таблица 1.

Численные исследование составных двухслойных треугольных пластин с комбинированными граничными условиями

Анализ полученных результатов показывает, что независимо от отношения толщин слоев фундаментальная зависимость (1) выполняется с точностью от +2,404 до -2,917% для двухслойной пластины с жесткими граничными условиями.

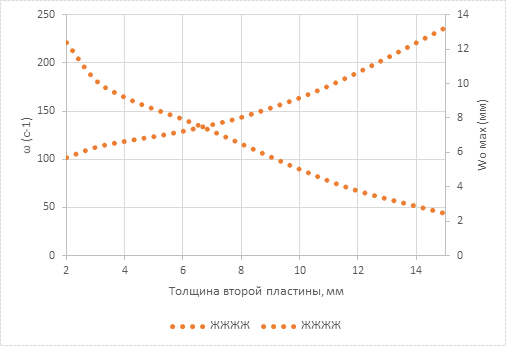
Рисунок 1. Взаимосвязь максимальных прогибов и частот собственных колебаний от отношения толщин двухслойной пластины