Исследование сил физического взаимодействия между магнитными полями постоянных магнитов
Конференция: XXX Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Секция: Физика магнитных явлений

XXX Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Исследование сил физического взаимодействия между магнитными полями постоянных магнитов
THE STUDY OF THE FORCES OF PHYSICAL INTERACTION BETWEEN THE MAGNETIC FIELDS OF PERMANENT MAGNETS
Denis Zakiev
Engineer, Volga State Technological University, Russia, Yoshkar-Ola
Andrey Margin
Student, Volga State Technological University, Russia, Yoshkar-Ola
Nikolay Krutskikh
Candidate of Technical Sciences, Associate Professor, Volga State Technological University, Russia, Yoshkar-Ola
Sergey Alibekov
Doctor of Technical Sciences, Professor, Volga State Technological University, Russia, Yoshkar-Ola
Аннотация. Приведены основные известные теоретические способы расчета постоянных магнитов и механических сил возникающих между их магнитными полями. Представлен способ исследования физических сил взаимодействия между постоянными магнитами и предложена обобщенная математическая функция описывающая зависимость возникающей силы от расстояния между постоянными магнитами. Представлен обобщенный способ исследования постоянных магнитов для разработки динамических магнитных опор и подвесов состоящих из магнитных сегментов позволяющих получать равномерное магнитное поле.
Abstract. The main known theoretical methods for calculating permanent magnets and mechanical forces arising between their magnetic fields are given. A method for studying the physical forces of interaction between permanent magnets is presented, and a generalized mathematical function is described that describes the dependence of the arising force on the distance between the permanent magnets. A generalized method for the study of permanent magnets for the development of dynamic magnetic supports and suspensions consisting of magnetic segments allowing to obtain a uniform magnetic field is presented.
Ключевые слова: исследования; коэрцитивная сила; магнитная муфта; магнитная опора; межмагнитное взаимодействие; постоянный магнит.
Keywords: research; coercive force; magnetic coupling; magnetic support; intermagnetic interaction; permanent magnet.
Исследование физических сил, возникающих между постоянными магнитами (ПМ), представляет интерес в связи с расчетом различных устройств и механизмов в которых используются ПМ, например, таких как магнитные муфты для бесконтактной передачи вращающего момента с ведущего вала на ведомый или магнитных подвесов и опор, обладающих значительными преимуществами по сравнению с традиционными опорами, повышающими общую надежность, долговечность и КПД механизма, вследствие сведения к минимуму сил механического трения в совокупности с отсутствием системы управления, т.к. использование ПМ устраняет необходимость наличия источника питания, что повышает автономную и эксплуатационную надежности системы в целом.
Для изготовления ПМ используют оксид железа Fe2O3 в соединении с ферритом бария или ферритом стронция, литые и металлокерамические сплавы на основе Fe-Al-Ni-Co (альнико), редкоземельные магниты (РЗМ) на основе SmCo (самарий-кобальт) и неодимовые NdFeB (неодим-железо-бор).
Достоинством ферритовых магнитов является низкая стоимость, устойчивость к размагничиванию и коррозионная стойкость. Как недостаток можно выделить хрупкость и низкие показатели остаточной индукции.
Магниты из сплава альнико характеризуются устойчивостью к нагреву, высокой коррозионной стойкостью, но обладают низкой коэрцитивной силой, вследствие чего легко размагничиваются.
Самарий-кобальтовые магниты (SmCo) при высокой технологичности, стойкости к высоким температурам и коррозионной стойкости, обладают высокой себестоимостью.
Неодимовые магниты (NdFeB) характеризуются высокой коэрцитивной силой при низкой стоимости, но обладают низкой коррозионной стойкостью, вследствие чего покрываются медью, никелем или цинком.
В соответствии с требованиями, предъявляемыми к современным изделиям заключающимся в низких себестоимости и весе, малых габаритных размерах и высокой надежности наиболее оптимальным является использование неодимовых магнитов (NdFeB).
Применение РЗМ приводит к компактности и миниатюрности и считается более целесообразным и экономически обоснованным [3].
Магниты делятся на классы (N33, N35, N38…), которые характеризуются величинами остаточной магнитной индукции, коэрцитивной силы, но в большей степени их мощностью, измеряемой в кДж/м3 и определяемой как относительная сила, которую необходимо приложить к магниту для отрыва его от листа (как правило стального) при соблюдении ряда условий по направлению прикладываемой силы, толщине, габаритам, состоянию поверхности и материалу, чем выше класс магнита, тем выше величина этой силы. К цифровой маркировке магнита добавляется буквенная, например N35M, которая обозначает верхний предел эксплуатационной температуры магнита. N (Normal) – до 80°С; M (Medium) – до 100°С; H (High) – до 120°С; SH (Super High) до 150°С; UH (Ultra High) – до 180°С; EH (Extra High) – до 200°С.
При расчете магнитных систем измерительных приборов и средств автоматики применяют три основных метода: метод отношений, метод размагничивающего фактора и метод эквивалентного соленоида. Метод отношений используют при расчете магнитов с арматурой, метод размагничивающего фактора – при расчете магнитов без арматуры в форме брусков и цилиндров, метод эквивалентного соленоида – при расчете магнитов без арматуры, выполненных из материалов с очень высокими значениями коэрцитивной силы и энергетического произведения, т.е РЗМ [3].
Метод эквивалентного соленоида основан на возможности рассматривать ПМ как однослойный соленоид, имеющий очень тонкую обмотку, по которой протекает намагничивающий ток. Условием эквивалентности является равенство магнитных моментов соленоида и магнита [3].
Расчет сил, возникающих при взаимодействии между ПМ, осуществляется методом эквивалентных диполей [3], [4]. Суть метода заключается в замене магнитов эквивалентными магнитными диполями. Условием эквивалентности является равенство значений магнитного момента у диполя и магнита:
qm∙l = Mm∙Vm , (1)
где qm – магнитный заряд; l – плечо эквивалентного диполя; Mm – намагниченность материала магнита; Vm – объем магнита.
Исходя из закона Кулона – модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними, при условии, что l << r0 , где r0 – расстояние между центрами диполей, сила F взаимодействия магнитов определяется как:
F = (3∙μ0∙Pm1∙Pm2)/(2∙π∙z4), (2)
где μ0 – магнитная постоянная; z – расстояние между магнитами; Pm1 и Pm2 – магнитные моменты первого и соответственно второго магнитов.
Вследствие того, что в формулу (2) в качестве характеристик магнитов входят только их магнитные моменты, она может быть применена для магнитов любой формы, при условии, чтобы расстояние между ними превышало их размеры, и их магнитные моменты были параллельны. Сила взаимодействия между ПМ обратно пропорциональна четвертой степени расстояния между ними, вследствие диполь-дипольного характера взаимодействия.
Для расчета сил межмагнитного взаимодействия, существуют различные программные продукты, например, ELCUT, в котором производится моделирование электромагнитных, тепловых и упругих полей методом конечных элементов. Решение задач магнитостатики могут проводиться как в линейной так и нелинейной постановках, в ELCUT используется уравнение Пуассона для векторного магнитного потенциала А (В = rot А, В – вектор магнитной индукции).
Силы отталкивания или притяжения между двумя ПМ равны [1], что также подтверждается расчетами выполняемыми в ELCUT, поэтому экспериментальные исследования взаимодействия между ПМ сводятся к нахождению силы притяжения.
Установка для проведения экспериментов изображена на Рис.1.
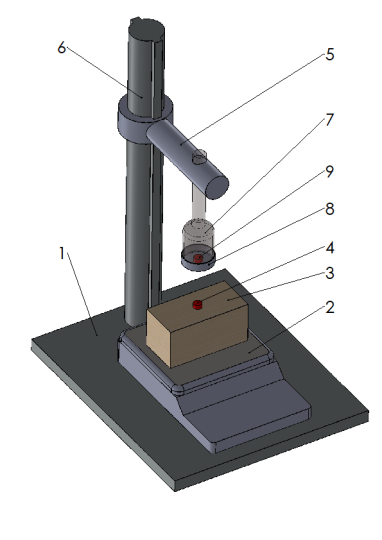
Рисунок 1. Экспериментальная установка
В нижней части, на основании 1, устанавливаются электронные весы 2 с точностью измерения 0,01г., на которых располагается груз 3 выполненный из немагнитного материала, на котором крепится исследуемый магнит 4. Вверху установки, на держателе 5, установленным на направляющей штанге 6 с возможностью осевого перемещения, крепится полая емкость 7, выполненная из немагнитного материала как и съемная крышка 8, в которую помещается второй образец исследуемого магнита 9.
Для проведения эксперимента на установку помещаются магниты 9 и 4 разноименными полюсами друг напротив друга. По показаниям весов фиксируется вес груза 3 с магнитом 4 и обозначается как базовый. После этого магнит 9 смещается вниз к магниту 4 на минимально возможное расстояние между ними для самоустановки магнита 9 относительно магнита 4 и соответственно совмещения их магнитных полей. После этого магнит 9 отводится в исходное положение и, с определенным дифференцированным шагом, начинает опускаться вниз, с одновременным снятием и записью, в каждой точке останова, показаний весов и расстояния между магнитами. Сила взаимодействия между ПМ определяется как разность, в каждой точке останова, изначального базового значения от текущего показания весов.

Рисунок 2. График зависимости сил притяжения двух геометрически равных РЗМ класса N38, в зависимости от расстояния между ними
Проведены исследования сил взаимодействия ряда РЗМ (NdFeB) отличающихся между собой как по форме, так и по размерам. По данным, полученным в результате проведенных опытов, были построены графические и математические зависимости. В качестве примера, на Рис.2, представлен график зависимости сил притяжения двух геометрически равных РЗМ класса N38, в зависимости от расстояния между ними.
В виде частичной выборки часть проводимых измерений сверялась с данными по расчетам полученными в программном пакете ELCUT_6.3Student выражаемых в пондеромоторной силе, как суммарной магнитной силе, действующей на тела, заключенных в заданном объеме. Расхождения с полученными данными в ELCUT и данными по эксперименту в среднем составило от 5 до 15%, что возможно связано как с погрешностью измерений и параметров материала, так и ограничением по числу узлов в сетке конечных элементов накладываемых в ELCUT и выбору контура интегрирования, что влияет на точность получаемых результатов.
Вычисление сил межмагнитного взаимодействия с помощью формулы (2), дает относительно точный результат только после введения в формулу поправочных коэффициентов. Неудобство ее использования также обусловлено отсутствием в ней четких граничных условий, т.к. известно что область ее применения ограничена определенным соотношением линейных размеров магнитов и расстоянием между ними.
Для всех выбранных пар исследуемых магнитов, в независимости от их формы и размеров, наиболее оптимальной, по методу наименьших квадратов [2], оказалась обобщенная математическая функция вида:
(a/x2) + b/x + c, (3)
которая показала хорошую сходимость с экспериментальными данными.
С учетом рассчитанных коэффициентов полученная квадратичная зависимость, для магнитов Рис.2, выглядит как: (17087,3/x2) – (523,8/х) + 3,8, где x – расстояние между магнитами. Данное уравнение дает достаточно точный результат начиная с расстояния между магнитами 37мм и ниже. Именно в этом пределе наблюдается наименьшее (менее 10%) расхождение между опытными и рассчитанными по зависимости (3) результатами.
Учитывая, что параметры магнитных материалов даются с точностью 5%, а принятые методы расчета магнитных проводимостей имеют ряд допущений, точность расчета магнитных систем в 10-15% считается удовлетворительной [3].
Для зависимости расстояния 37мм и выше до момента начала физического контакта магнитных полей, также характерна квадратичная зависимость. В результате обобщенные результаты измерений, для каждой пары магнитов, представляются в виде системы состоящей из двух уравнений, граничные условия выбора между которыми определяются нелинейной зависимостью их суммарного объема от расстояния между ними и которые могут быть выражены, например, в виде степенного полинома. В полученную систему уравнений, для расчета взаимодействия между магнитами других классов, вводятся поправочные коэффициенты на величину остаточной магнитной индукции.
В результате, расчет систем межмагнитного как статического, так и динамического взаимодействия, с учетом возросших скоростей расчета и обработки информации процессорной техникой, может быть представлен в виде обобщения получаемых эмпирических систем уравнений, посредством использования различных алгоритмов таких языков программирования как С++, С# или Java, в единой математической модели.
Полученный выше результат исследований может быть применен к магнитным муфтам, для расчета передаваемого ими крутящего момента. Для систем, состоящих из магнитных опор и подвесов, работающих не в статическом режиме, представляет интерес экспериментальные исследования сил возникающих между магнитами при наличии градиента смещения между их плоскостями симметрии, которые выражаются функциональной зависимостью F(x, ∆r, V), где F – величина возникающей силы, х – расстояние между магнитами, ∆r – величина ассиметричного смещения в системе ПДСК по плоскости взаимодействия, V – объем магнита, или безразмерная величина характеризующая геометрические параметры ПМ.
Данные исследования позволяют с достаточной степенью точности рассчитать, например, системы магнитных опор или подвесов, выполненных не из сплошного ПМ, а набираемых из магнитных сегментов. Величины полученных сил, в совокупности с методами 3D моделирования позволяют определить общее оптимальное количество магнитных пар в системе и выполнить их оптимальную расстановку, в которой сведены к минимуму «провалы» (неравномерность) магнитного поля за счет их перекрытия соседними и противолежащими парами ПМ.
Проведенное исследование позволяет повысить КПД магнитной опоры (подвеса), снизить ее себестоимость, отказаться от ограничений по привязке к существующим размерам сплошных ПМ при проектировании магнитных опор, или дорогостоящего изготовления ПМ нестандартного размера, а также позволяет определить общее оптимальное количество магнитных пар в системе и выполнить их оптимальную расстановку с целью уменьшения «провалов» (неровномерности) магнитного поля за счет перекрытия с соседними и противолежащими парами постоянных магнитов.


