Программа для имитационного моделирования физических процессов

Аннотация. При отсутствии серьезных навыков программирования у студентов первых курсов возникает необходимость разработки программного обеспечения для поддержки лабораторного практикума. В статье рассматривается схема упругого взаимодействия между телами без учета внешних сил с использованием метода Эйлера. 

Abstract. In the absence of serious programming skills of students there will need to develop software to support laboratory practical work. The article discusses the scheme of elastic interaction between bodies without external forces using the Euler method.

Ключевые слова: упругое столкновение; сила взаимодействия; моделирование; визуализация.

Keywords: elastic collision; force of interaction; modeling; rendering.

Программа разработана для имитационного моделирования упругого столкновения тел, предназначена для студентов 1-ого и 2-ого курса кафедры ИСКМ ВолГУ и будет помогать в изучении дисциплины «Физические основы современных технологий». Такое программное обеспечение может использоваться студентом в качестве основы при разработке программ численного моделирования.

Численный алгоритм реализован в среде MS Visual Studio и написан на языке C++ с использованием графической библиотеки OpenGL и GLUT.

В основе решения задачи нахождения силы взаимодействия между телами лежит II закон Ньютона

здесь  – масса  - го тела,  – его ускорение,  – сила, действующая на  - е тело со стороны всех других тел.

По определению ускорение есть производная от скорости по времени

где  – скорость k-го тела.

Применяем метод Эйлера для нахождения скорости и положения тела [3]

Выражаем скорость на следующем шаге по времени  

Выражаем положение тела на следующем шаге по времени

В работе рассмотрена схема упругого взаимодействия  тел без учета внешних сил.  Чтобы рассчитать силу взаимодействия для каждого тела  со стороны всех остальных тел нужно высчитать сумму

здесь  - сила взаимодействия между  и  телом,  – общее количество тел.

Так как моделируется абсолютно упругое столкновение, нужно рассчитать силу упругости между телами

здесь  – коэффициент упругости,  – расстояние, на которое изменяется исходная длина тела.

Поставим, что  – глубина проникновения тел друг в друга,  - индекс тела,  - индекс соседнего тела. Тогда формула будет выглядеть так

Глубину проникновения  можно найти по формуле 

где  – радиус -ого тела,  – радиус -ого тела,  - расстояние между телами.

Для того чтобы вычислить глубину проникновения тел нужно рассчитать расстояние между телами по формуле

Так как расчёт идет в декартовой системе координат необходимо вычислить силу для x и y компонент. Для каждого тела  вычисляем две компоненты силы

Таким образом, подставляем значения в формулу (1) и вычисляем силу взаимодействия.

Алгоритм работы программы

- Задаем начальные параметры, инициализируем тела.

- Для каждого тела k рассчитываем скорость, положение и силу взаимодействия с другими телами на шаге по времени Δt.

- Записываем полученные значения в файл.

- Если тело достигло края расчетной области, рассчитываем зеркальное отражение.

При запуске программы на экране появляется окно визуализации. Окно визуализации содержит наблюдаемую сцену, тела и некоторые параметры системы. Интерфейс работы программы представлен на рисунке 1.

Рисунок 1. Интерфейс работы программы

Проведем проверку использованного метода путем исследования вычислений на закон сохранения механической энергии

здесь  и - скорость первого и второго тела до столкновения,  и  - скорость первого и второго тела после столкновения.

 Согласно классической механике полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной

здесь  - кинетическая энергия до удара,  - кинетическая энергия после удара. 

Рассмотрим частный случай, в котором два тела имеют одинаковую массу, одно тело движется с постоянной скоростью в сторону другого. На рисунке 2 находится график изменения полной механической энергии.

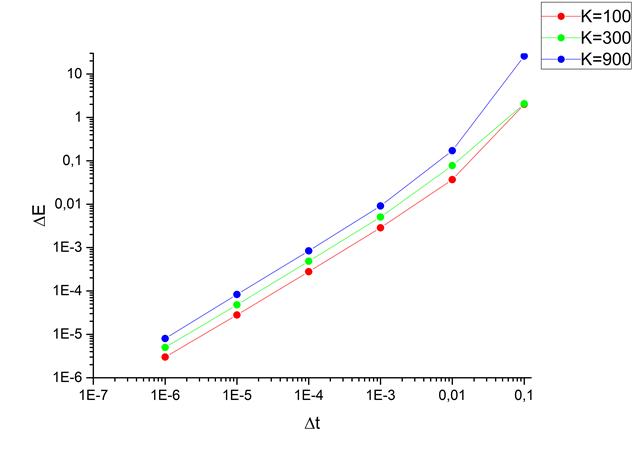
Рисунок 2 . График изменения полной механической энергии ().  - шаг по времени,  - коэффициент упругости

Из этого графика следует, что метод имеет погрешность, чем больше значение , K, тем сильнее видно отклонение.

Существенным недостатком простого метода Эйлера является слишком большая погрешность. Данный факт хорошо виден на рисунке 2. Улучшить приближение можно при помощи уменьшения шага по времени.

Проведенное исследование показывает, что при работе с программой можно решать ряд задач: исследование системы на закон сохранения энергии; влияние коэффициента упругости и шага по времени на точность вычислений; построение и анализ графиков на основе данных, записанных в файл.