Применение Q-критерия Розенбаума для сравнения рейтинговых баллов

Application Q-criterion Rosenbaum for comparison rating points

Irina Ushakova

undergraduate Federal State Budget Educational Institution of Higher Education «Sholom-Aleichem Priamursky State University», Russia, Birobidzhan

Аннотация. В статье представлено применение непараметри­ческого критерия Q-Розенбаума для сравнения результатов обучения (рейтинговых баллов) студентов 1 курса технических направлений подготовки по дисциплине «Математический анализ».

Abstract. The article presents the application of the non-parametric Q-Rosenbaum criterion for comparing the results (rating points) of the first-year students' training in the technical areas of training in the discipline "Mathematical Analysis".

Ключевые слова: рабочая тетрадь; презентации с динамической компьютерной визуализацией; критерий Q-Розенбаум.

Keywords: workbook; presentation computer with dynamic visualization; criterion Q-Rosenbaum.

Математическая статистика играет важную роль при статис­тическом исследовании вероятностных явлений. В ней в полной мере находят применение такие методы как теория статистической проверки вероятностных гипотез, теория статистической оценки распределений испытаний.

Статистическое описание совокупности объектов занимает промежуточное положение между индивидуальным описанием каждого из объектов совокупности, с одной стороны, и описанием совокупности по её общим свойствам, совсем не требующим её расчленения на отдельные объекты − с другой. По сравнению с первым способом статистические данные всегда в большей или меньшей степени обезличены и имеют лишь ограниченную ценность в случаях, когда существенны именно индивидуальные данные (например, учитель, знакомясь с классом, получит лишь весьма предварительную ориентировку о положении дела из одной статистики числа выставленных его предшественником отличных, хороших, удовлетворительных и неудовлетворительных оценок). С другой стороны, по сравнению с данными о наблюдаемых извне суммарных свойствах совокупности статистические данные позволяют глубже проникнуть в суть дела. Например, данные гранулометри­ческого анализа породы (то есть данные о распределении образующих породу частиц по размерам) дают ценную дополнительную информацию по сравнению с испытанием нерасчленённых образцов породы, позволяя в некоторой мере объяснить свойства породы, условия её образования и прочее.

Следовательно, методы математической статистики позволяют оценить параметры имеющихся закономерностей, проверить те или иные гипотезы об этих закономерностях.

В федеральных образовательных стандартах третьего поколения высшей школы указано на возможность применять электронное обучение и дистанционные образовательные технологии. Для реализации данного положения разработаны рабочая тетрадь и курс презентаций, в котором используются ролики с компьютерной визуализацией по математическому анализу для студентов 1 курса технических направлений подготовки. Рабочая тетрадь позволяет студентам меньше времени тратить на написание лекций, так как основные теоретические положения в ней представлены, остаётся только вписывать расчёты и формулы. Презентации разработаны для всех разделов курса математического анализа с использованием роликов, которые позволяют наглядно демонстрировать студентам теорети­ческий материал: что происходит с данной функцией на конкретном промежутке, при её растяжении и сжатии, или как изменяется предел функции при изменении значений переменной.

В исследовании приняли участие студенты 1 курса двух академи­ческих групп технического направления подготовки. В одной из групп изложение материала происходило традиционным способом, в другой – с применением динамической компьютерной визуализации. После изучения курса математического анализа в осеннем семестре сравнили результаты обучения (в рейтинговых баллах) студентов каждой группы, используя непараметрический Q-критерий Розенбаума для несвязных выборок. Критерий используется для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. В каждой из выборок должно быть не менее 11 испытуемых. Данный критерий основан на сравнении двух упорядоченных, но не обязательно равных по численности рядов наблюдений [1, с. 14].

Баллы студентов, изучающих математический анализ тради­ционным способом: 0; 0; 0;1; 1; 4; 5; 5; 6,5; 8; 11; 15; 22,5; 25; 38; 39;40.

Баллы студентов, изучающих математический анализ с приме­нением динамической компьютерной визуализации: 2; 3; 5; 7; 10; 18,5; 32,5; 38; 46,5; 48,5; 54,5; 55,5; 62; 66.

Нулевая гипотеза является проверяемым предположением, которое обычно формулируется как отсутствие различий, отсутствие влияния фактора, отсутствие эффекта. Противоположное предположение является конкурирующей или альтернативной гипотезой, которая выдвигается для опровержения нулевой гипотезы.

Гипотезы:

H₀ − баллы студентов, изучающих математический анализ с применением динамической компьютерной визуализации, не превышают баллы студентов, изучающих математический анализ традиционным способом.

H₁ − баллы студентов, изучающих математический анализ с применением динамической компьютерной визуализации, превышают баллы студентов, изучающих математический анализ традиционным способом.

Решение.

Считаем выборкой один ту, в которой баллы выше, а выборкой два − ту, в которой баллы ниже. Следовательно, выборка один – это выборка студентов, изучающих математический анализ с применением динамической компьютерной визуализации, а выборка два – это выборка студентов, изучающих математический анализ традиционным способом.

Согласно Q-критерию Розенбаума находим максимальное значение выборки два и подсчитываем количество значений в выборке один, которые выше этого значения, обозначаем полученную величину буквой T.

Определяем минимальное значение выборки один и подсчитываем количество значений в выборке два, которые ниже этого значения, обозначаем полученную величину буквой S.

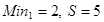
Находим эмпирическое значение по формуле . 

Вычисляем критические значения по таблице, используя объем выборок n₁ =14, n₂=17,

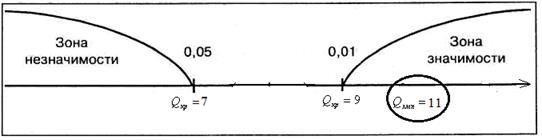
Рисунок 1. Ось значимости

Итак, эмпирическое значение попало в зону значимости, следова­тельно, принимается альтернативная гипотеза на уровне значимости 0,01. Значит, баллы студентов, изучающих математический анализ с применением динамической компьютерной визуализации, превышают баллы студентов, изучающих математический анализ традиционным способом.