Алгоритм обнаружения и устранения ошибок измерения во временных рядах со свойствами персистентности и неподчинения нормальному закону распределения
Конференция: VI Международная заочная научно-практическая конференция "Научный форум: технические и физико-математические науки"
Секция: Информатика, вычислительная техника и управление

VI Международная заочная научно-практическая конференция "Научный форум: технические и физико-математические науки"
Алгоритм обнаружения и устранения ошибок измерения во временных рядах со свойствами персистентности и неподчинения нормальному закону распределения
The algorithm for detecting and eliminating measurement errors in time series with persistence and non-obeying the law of normal distribution
Viacheslav Petrenko
сandidate of technical sciences, associate professor, North Caucasus Federal University, SKFU, Russia, Stavropol
Alesya Sidorchuk
graduate student, North Caucasus Federal University, SKFU, Russia, Stavropol
Аннотация. В предлагаемом алгоритме ошибка измерения во временном ряде влечет за собой потерю такого внутреннего свойства, как персистентность значений. Для устранения ошибок измерения в методе предлагается заменить его на спрогнозированную величину с помощью адаптации уточненного метода Брауна. Алгоритм применим для временных рядов быстропротекающих процессов, распределение которых не подчиняется нормальному закону.
Abstract. In the proposed algorithm, the measurement error in the time series entails the loss of such an intrinsic property as the persistence of the values. To eliminate measurement errors in the method, it is proposed to replace it with the predicted value by adapting the refined Brown method. The algorithm is applicable to time series of fast processes, the distribution of which does not obey the normal law.
Ключевые слова: временной ряд; ошибка измерения; персистентность, неподчинение нормального закону распределения; показатель Херста; прогнозирование; уточненный метод Брауна
Keywords: Time series; measurement error; persistence, non-compliance with the normal distribution law; Hurst rate; forecasting; refined method of Brown.
Своевременное выявление и устранение ошибок измерения во временных рядах наблюдаемых процессов является актуальной проблемой практически всех систем ситуационного управления [12]. Ошибочные значения временного ряда оказывают существенное влияние на основные характеристики временного ряда. Ошибочные значения наблюдений могут возникнуть по техническим причинам: ошибки при агрегировании и дезагрегировании показателей, при передаче информации и др. [11].
В настоящей работе предлагается алгоритм обнаружения и устранения ошибок измерения во временных рядах со свойствами персистентности [2; 7;8] и неподчинения закону нормального распределения [9]. Свойство персистентности означает наличие долговременной коррелированности настоящих и предыдущих значений временного ряда. Не подчинение закону нормального распределения происходит из-за стремительного развития многих наблюдаемых процессов.
Предлагаемый алгоритм обнаружения и устранения ошибок измерения во временных рядах со свойствами персистентности и неподчинения закону нормального распределения состоит из 4 этапов:
1) проверка временного ряда на подчинение/неподчинение закону нормального распределения;
2) проверка временного ряда на наличие или отсутствие персистентности;
3) обнаружение ошибочных значений;
4) устранение ошибочных значений.
На этапе 1 для проверки временного ряда на подчинение/неподчинение закону нормального распределения предлагается воспользоваться тестом Шапиро-Уилка [1]. Тест Шапиро-Уилка применим при ![]() и основан на упорядоченных наблюдениях. Процедура проверки следующая: выдвигается нулевая гипотеза о нормальном распределении генеральной совокупности. Значения временного ряда
и основан на упорядоченных наблюдениях. Процедура проверки следующая: выдвигается нулевая гипотеза о нормальном распределении генеральной совокупности. Значения временного ряда ![]() необходимо упорядочить по возрастанию
необходимо упорядочить по возрастанию ![]() , где
, где ![]() . Вычисляется промежуточная сумма
. Вычисляется промежуточная сумма ![]() по формуле
по формуле ![]() , где
, где ![]() , если
, если ![]() четно, и
четно, и ![]() , если
, если ![]() нечетно;
нечетно; ![]() – специальные табличные коэффициенты [1]. Рассчитывается наблюдаемое значение критерия Шапиро-Уилка
– специальные табличные коэффициенты [1]. Рассчитывается наблюдаемое значение критерия Шапиро-Уилка ![]() , где
, где ![]() ,
, ![]() – объем выборки,
– объем выборки, ![]() – выборочный центральный момент второго порядка. Наблюдаемое значение
– выборочный центральный момент второго порядка. Наблюдаемое значение ![]() сравнивается с критическим значением
сравнивается с критическим значением ![]() , которое находится по таблице критических точек критерия Шапиро-Уилка в зависимости от объёма выборки и уровня значимости. Если
, которое находится по таблице критических точек критерия Шапиро-Уилка в зависимости от объёма выборки и уровня значимости. Если ![]() , то нулевая гипотеза о нормальном распределении результатов принимается; при
, то нулевая гипотеза о нормальном распределении результатов принимается; при![]() она отвергается.
она отвергается.
На этапе 2 для проверки временного ряда на наличие или отсутствие персистентности предлагается проводить анализ значений показателя Херста вдоль временного ряда. Рассчитать значения показателя Херста можно по методу нормированного размаха [2, 7], идея которого состоит в следующем. Для временного ряда ![]() рассматриваются начальные отрезки
рассматриваются начальные отрезки ![]() ,
, ![]() . Для каждого начального отрезка нужно вычислить текущие средние
. Для каждого начального отрезка нужно вычислить текущие средние 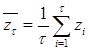 . Далее, вычислить накопленные отклонения
. Далее, вычислить накопленные отклонения ![]() и размах
и размах ![]() . Нормированный размах представляет собой безразмерную величину и находится по формуле
. Нормированный размах представляет собой безразмерную величину и находится по формуле 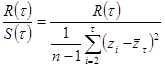 . Херстом введено эмпирические соотношение
. Херстом введено эмпирические соотношение ![]() ,где
,где ![]() – показатель Херста,
– показатель Херста, ![]() – среднее квадратичное отклонение внутри начального отрезка
– среднее квадратичное отклонение внутри начального отрезка ![]() . Для вывода показателя Херста
. Для вывода показателя Херста ![]() следует прологарифмировать обе части выражения
следует прологарифмировать обе части выражения ![]() :
: , где
, где ![]() . В результате получим формулу показателя Херста
. В результате получим формулу показателя Херста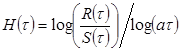 . В [2] рекомендовано
. В [2] рекомендовано ![]() брать по основанию 10, а константе
брать по основанию 10, а константе ![]() присвоить значение 0,5. В результате имеем формулу расчета показателя Херста для каждого начального отрезка
присвоить значение 0,5. В результате имеем формулу расчета показателя Херста для каждого начального отрезка ![]() :
: ![]() . Для ответа на вопрос, является ли временной ряд персистентным, рекомендуется получить усредненное значение показателя Херста
. Для ответа на вопрос, является ли временной ряд персистентным, рекомендуется получить усредненное значение показателя Херста ![]() . Если
. Если ![]() , то временной ряд персистентен, в противном случае неперсистентен.
, то временной ряд персистентен, в противном случае неперсистентен.
На этапе 3 для обнаружения ошибочных значений предлагается сформировать ![]() -траекторию из вычисленных значений показателя Херста
-траекторию из вычисленных значений показателя Херста ![]() ,
, ![]() . Точка
. Точка ![]() временного ряда
временного ряда ![]() будет считаться ошибочным значением, если, начиная с нее
будет считаться ошибочным значением, если, начиная с нее ![]() -траектория уходит из области персистентности и больше не возвращается, т.е.
-траектория уходит из области персистентности и больше не возвращается, т.е. ![]() ,
,![]() .
.
На этапе 4 устранение ошибочных значений предлагается осуществлять путем их замены на прогнозные величины. Для прогнозирования ошибочного значения предлагается использовать адаптацию уточненного метода Брауна [10]. Классический метод Брауна имеет расчетную формулу ![]() ,
,
где: ![]() – коэффициент сглаживания из интервала
– коэффициент сглаживания из интервала ![]() . Этот коэффициент следует выбирать так, чтобы относительные отклонения прогнозных величин от фактических значений были минимальны
. Этот коэффициент следует выбирать так, чтобы относительные отклонения прогнозных величин от фактических значений были минимальны  . В уточненном методе Брауна коэффициент сглаживания
. В уточненном методе Брауна коэффициент сглаживания ![]() находится в интервале
находится в интервале ![]() и рассчитывается по формуле
и рассчитывается по формуле ![]() . После подстановки коэффициента
. После подстановки коэффициента ![]() в формулу (3), имеем расчетную формулу уточненного метода Брауна
в формулу (3), имеем расчетную формулу уточненного метода Брауна ![]() , где
, где ![]() – усредненное значение показателя Херста. Адаптация уточненного метода Брауна состоит в следующем: для получения прогноза ошибочного значения
– усредненное значение показателя Херста. Адаптация уточненного метода Брауна состоит в следующем: для получения прогноза ошибочного значения ![]() следует брать не усредненную величину показателя Херста
следует брать не усредненную величину показателя Херста ![]() , а отдельные значения показателя Херста в точках
, а отдельные значения показателя Херста в точках ![]() и
и ![]() :
: ![]() и
и ![]() . Прогноз ошибочного значения в этом случае можно осуществить по формуле
. Прогноз ошибочного значения в этом случае можно осуществить по формуле ![]() . При замене ошибочного значения на прогнозную величину получаем новый временной ряд
. При замене ошибочного значения на прогнозную величину получаем новый временной ряд ![]() . Если во временном ряде имеется несколько подозрительных ошибочных значений, то следует применять предлагаемый метод несколько раз. Начинать необходимо с наиболее ранее встречающегося подозрительного значения, после его подтверждения и устранения нужно перейти к следующему и т.д. до конца временного ряда.
. Если во временном ряде имеется несколько подозрительных ошибочных значений, то следует применять предлагаемый метод несколько раз. Начинать необходимо с наиболее ранее встречающегося подозрительного значения, после его подтверждения и устранения нужно перейти к следующему и т.д. до конца временного ряда.
Предлагаемый алгоритм позволит своевременного обнаруживать и устранять ошибки измерения во временных рядах наблюдаемых процессов в системах ситуационного управления. Технически реализовать этот алгоритм можно в модуле предварительной обработки данных с использованием предложенных в работах [6; 3; 4; 5] вычислительных устройств сумматоров, инверторов, умножителей, мультиплексора.

