Роль математического образования в формировании функциональной грамотности обучающихся

В настоящее время вопрос развития уровня функциональной грамотности наравне с повышением качества образования [1-2] занимает одно из главных мест в образовательном процессе. Научить молодое поколение решать стандартные и нестандартные жизненные задачи в различных сферах жизнедеятельности на основе полученных знаний является одной из основных задач учителя.

Вопросу функциональной грамотности, зачем она нужна, пути её развития посвящено много работ, например [3-6]. Функциональной грамотности посвящено исследование Международной оценки образовательных достижений учащихся – PISA (Programme for International Student Assessment). В исследовании оценивается, главным образом, способность использовать полученные знания, умения и навыки для решения самых разных жизненных задач. Основные направления исследования: читательская грамотность, математическая и естественнонаучная. Министерством просвещения был разработан проект «Мониторинг формирования функциональной грамотности».

Основной вывод - процесс формирования функциональной грамотности должен быть непрерывным, задачи на развитие функциональной грамотности должны присутствовать как непосредственно в учебном процессе, так и дополнительное и предпрофессиональное образовании учащихся.

Рассмотрим следующую математическую модель - уровень функциональной грамотности U_ф можно представить формулой

,

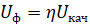где U_кач – уровень качества образования, 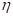 – коэффициент способности использования приобретенных знаний.

Уровень качества образования U_кач определим следующим образом:

,

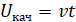где v – коэффициента качества подачи информации, t – время подачи информации.

Предположим, что данный коэффициент зависит от уровня методики повышения функциональной грамотности и объема материала (задач) по её повышению, а также от коэффициента качества подачи информации v.

На основании этого коэффициент 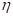 можно представить в следующем виде:

.

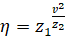Здесь параметры z1, z2 задают уровни методики и объёма материала. Они принимают значения в диапазоне от 0 до 1.

Чтобы уровень функциональной грамотности U_ф был наибольшим необходимо, чтобы было принято максимальное значение функция .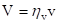

Значения коэффициента качества подачи информации, при котором достигается максимальный уровень функциональной грамотности, приведены на рисунке: сплошная линия соответствует случаю: z1=0,5; параметр z2 изменяется от 0 до 1; штриховая линия: z2=0,5; z1 изменяется от 0 до 1.

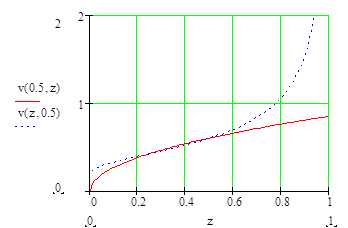
Рисунок. Значения коэффициента качества подачи информации, при котором достигается максимальный уровень функциональной грамотности

Из рисунка видно, что при средних значениях параметров z1 и z2 методика и объём задач одинаково влияют на уровень функциональной грамотности. Однако, при увеличении этих значений, повышении качества методики повышения функциональной грамотности более значительно влияют на её уровень.

Конечно же, это особенности модели, но здесь есть и рациональное зерно – для повышения уровня функциональной грамотности надо более тщательно подходить к подбору материала (задач) для развития функциональной грамотности.

Рассмотрим математическую грамотность, как часть функциональной грамотности, позволяющую учащимся использовать и применять математические знания. Причем использование разделяется на два направления. При стандартном направлении мы просто применяем математические навыки вычислений в повседневной жизни и при изучении других предметов. Другое направление связано не с применением навыков, а непосредственно с развитием математических способностей, с использованием математики для решения проблем, анализа ситуаций, разработки путей решения и выдачи практических рекомендаций. Данный подход связан с развитием логического мышления, умением анализировать, обобщать, выделять основное, главное, критически мыслить.

Что можно предложить в этом направлении? Тут нельзя забывать о наработках советского периода - занковская система для начальных классов, обучение ТРИЗ-технологиям, которые учили детей мыслить, рассуждать, поступать нешаблонно.

Так же как нельзя лучше подходит для повышения математической грамотности научно-практическая деятельность школьников в рамках Всероссийской конференции «Шаг в будущее» на всех её этапах от школьного до всероссийского. В этом контексте математика консолидирует другие направления функциональной грамотности - компьютерную и естественно-научную грамотность. Математическая грамотность позволяет решать различные прикладные задачи на основе анализа исходных данных, построения математической модели, разработки и реализации численного алгоритма, моделирующего стратегию решения задачи, анализа и выдачи практических рекомендаций. Некоторые конкретные примеры таких задач, решенные школьниками под моим руководством, в рамках участия во Всероссийской конференции «Шаг в будущее» приведены ниже:

Задача 1. Построена на примере компьютерной игры «Братья Пилоты: По следам полосатого слона». Сценарий игры выдержан в стиле пародийного детектива, в котором сыщики Братья Пилоты вынуждены искать выход из любых ситуаций, возникающих в ходе расследования похищения слона из зоопарка. По ходу игры необходимо решить занимательную головоломку − открыть холодильник, закрытый хитрым замком, который открывался поворотом ручек замка, при повороте которых их расположение изменялось по некоторому правилу. Для открытия замка требовалось получить нужное расположение ручек замка. В пособии по компьютерным играм решения данной головоломки приведено не было, т. е. автору пособия оно не было известно. Для решения данной задачи пришлось провести некоторые интересные исследования. Была построена  математическая модель замка холодильника, представляющая собой таблицы, состоящие из n строк и n столбцов. Элементы таблицы принимают значения «1» и «-1». Для данного класса объектов была введена операция произведения и «умножением на элемент» a_ijA. Результатом исследований было написание программы игрушки, которая помогла изучить поведение замка и получить практические рекомендации по открытию холодильника.

Задача 2. Рассмотрен учебный процесс в отдельно взятом классе. Предметом исследования было качество обучения учащихся. Результатом исследования было построение математической модели; проведение численного эксперимента; анализ результатов

Группа учащихся по успеваемости делилась на три подгруппы: С – слабая; В – средняя; А – сильная. В процессе обучения учащиеся могут переходить из одной группы в другую. Группа содержит N человек.

В задаче моделируется процесс изменения численности трех подгрупп по успеваемости в отдельно взятом классе. Для решения задачи была предложена математическая модель, которая выражает зависимость численности подгрупп от их численности на предыдущем шаге.

Задача 3. Каждый день миллионы людей садятся за руль личного автомобиля и вливаются в транспортный поток. Машины в потоке едут неравномерно – то приближаясь к едущей впереди машине, то слегка удаляясь от нее. Если кто-то зазевался и подъехал слишком близко, то приходится нажимать на тормоз. И если скорость будет уменьшена ниже определенной критической отметки, следующая машина вынуждена притормозить сильнее и так далее. В результате мы имеем аварийную ситуацию и, в лучшем случае, поток машин останавливается почти полностью.

Целью данной работы была разработка и реализация численного алгоритма, моделирующего стратегию движения автомобиля в транспортном потоке.

Предложенная математическая модель позволяет определять оптимальное расстояние между машинами, чтобы избежать аварийной ситуации, и учитывать нелинейность ускорения. Для исследования потока машин как взаимосвязанного механизма модель реализована для замкнутой траектории. Рассмотрены тестовые примеры разгона и остановки потока машин.

Модель реализована в виде расчетной программы на Visual Basic for Applications в среде Excel, позволяющая рассматривать изменение положения машин с заданным интервалом времени.

Данный алгоритм можно использовать для создания прибора определения оптимальной скорости на основе лазерных дальномеров со связью с ПК.

Задача 4. Вода является важным элементом для существования жизни. Человек на 70-75% (в зависимости от возраста) состоит из воды. Вода, которую мы пьем, обеспечивает все биохимические процессы в организме. Поэтому качество воды даже важнее, чем качество пищи, которую мы едим. Да и пищу мы готовим прежде всего на воде.

Очевидно, что проблема контроля качества и очистки воды стоит в наше время очень остро.

Очищать воду можно методом частичного замораживания. Дело в том, что в первую очередь замерзает наиболее пресная и чистая часть воды, а после - содержащая соли и различные примеси.

Учитывая положительное влияние талой воды на организм человека, некоторые геронтологи выдвинули предположение, что одной из причин большого количества долгожителей в Якутии и на Кавказе является преимущественное потребление талой воды. Ведь ничего общего в этих отдаленных друг от друга районах нет, за исключением того, что люди там пьют воду, образовавшуюся в результате таяния снега или льда.

Целью данной работы было установление влияния способа замораживания питьевой воды в домашних условиях на ее качество для выбора лучшего из них в зависимости от сезона года.

Для этого были сформулированы  и решались следующие задачи:

1.Проведение натурного эксперимента по замораживанию воды в домашних условиях.

2. Проведение в лабораторных условиях химического анализа воды.

3. Анализ результатов и разработка рекомендаций.

Задача 5. Человек, как биологический объект, в своей ежедневной жизни подвержен влиянию биологических ритмов в полной мере. Биоритмы воздействуют на все аспекты его жизнедеятельности: активность, выносливость, уровень иммунитета, мыслительные способности и прочие качества. В Европе многие специалисты свободных по графику профессий стали изучать свои ритмы и жить по схеме – работать по максимуму, когда работается и отдыхать, когда работа ну не идет и все. Многие из них оставляют положительные отзывы о программах расчетов биоритмов. Хотя кто знает, может это просто психосоматика срабатывает. Как говорят, не стоит верить на слово – мы решили убедиться во всем лично!

Целью данной работы стало исследование данного вопроса – исследование связи биологических ритмов на количество баллов при сдаче ГИА по математике.

Для решения исследуемой поставленной проблемы были поставлены следующие задачи исследований:

1. Составить модель и написать программу расчета биоритмов конкретного человека от указанного дня отсчета на задаваемый промежуток времени.

2. Подготовить данные для оценки влияния биологических ритмов на примере школьного экзамена ГИА по математике.

3. Разработка критерия оценки связи сдачи школьниками экзамена ГИА с их биологическими ритмами школьников.

4. На основании разработанного критерия ответить на вопрос о влиянии биологических ритмов на сдачу экзамена для рассматриваемого класса.

Задача 6. Многочисленными опытами было обнаружено, что при изменении размеров образцов из различных материалов их свойства (в том числе и прочность) меняются. Важность этой проблемы для горной промышленности состоит в том, что все горно-инженерные воздействия на массив должны выполняться на основе достоверных знаний о свойствах и состоянии горных пород, слагающих этот массив. При этом, главная сложность состоит в том, чтобы перенести результаты лабораторных испытаний породных образцов малых размеров на достаточно большие участки массива сложного структурного строения.

Целью работы было исследование связи фрактальной размерности и масштабного эффекта для оценки прочности образцов горной породы и руды

Задачи исследования:

1. Оценка влияния масштабного эффекта на прочность горной породы .

2. Разработка экспериментального способа определения фрактальной размерности разлома, полученного при расколе куска горной породы.

3. Оценка зависимости фрактальной размерности разлома от характерного размера куска, которая помогает прогнозировать прочность в массиве.

Задача 7. Рассмотрим задачу равновесия жесткой плиты. Сначала рассматривалась задача расстановки опор, а затем расстановки весовых точек нагрузки. При расстановке весовых точек нагрузки особое место занимала задача расстановки двух точек с заданными весами. Определялась область возможного расположения одной весовой точки, при котором её можно было бы уравновесить другой, то есть, если первая точка находится внутри данной области, то на треугольнике существует точка, такая что, если в неё поместить вторую весовую точку, то реакции опор останутся равными.

Целью данной работы было нахождение оптимального расположения весовых точек на треугольнике. Рассматривались следующие задачи:

1. Оптимальное расположение опор.

2. Оптимальное расположение нагрузки.

3. Определение области возможного приложения нагрузки для случая двух грузов.

4. Написание программы в среде MathCAD для расчета и отображения данной области.

Задача 8. Оптимальная работа буфета. Некоторые учащиеся не хотят питаться в столовой по разным причинам, не которым просто не хватает. Поэтому кроме домашних завтраков у них остается единственный вариант – пойти в буфет.

Для исследования работы буфета были решены следующие задачи:

-  тестирование среди учащихся средней и старшей школы на предмет посещения буфета;

-  мониторинг работы буфета;

- написана программа, моделирующую  буфетную очередь, в которую случайным образом вводились задержки на расспросы и попытки покушать без очереди.

В результате работы было выдача рекомендаций по работе буфета на основе желающих питаться в нем и его пропускной способности.

Увлеченность творческой деятельностью приносит свои плоды и повышает качество математического образования, и как следствие уровень функциональной грамотности, что позволяет нашим выпускникам успешно учиться в ведущих технических вузах России.