СУЩЕСТВОВАНИЕ ОБЩЕЙ РЕШЁТКИ ДЛЯ ДЕВЯТИ ЭЛЕМЕНТОВ НА МНОЖЕСТВЕ ИЗ ПЯТИ ЭЛМЕНТОВ, ИМЕЮЩИХ ВЕРНХНЮЮ И НИЖНЮЮ ГРАНИЦУ.
Секция: 6. Математические науки

XXXIV Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
СУЩЕСТВОВАНИЕ ОБЩЕЙ РЕШЁТКИ ДЛЯ ДЕВЯТИ ЭЛЕМЕНТОВ НА МНОЖЕСТВЕ ИЗ ПЯТИ ЭЛМЕНТОВ, ИМЕЮЩИХ ВЕРНХНЮЮ И НИЖНЮЮ ГРАНИЦУ.
Аннотация. В данной работе исследуется метод построение решётки для девяти элементов: a,b, c, a˅c, b˅c, a˄c, b˄c, a˄ (b˅c), b˅(a˄c), при условии, что b<a и аксиомы теории решётки действительны. Целью работы является доказательство существование такой решётки и построение её диаграмм.
Ключевые слова: Определение: Решётка – чaстичнo yпоpядoченнoe мнoжecтвo, в котором каждое двухэлементное подмножество имеет как точную верхнюю (sup), так и точную нижнюю (inf) грани. Отсюда вытекает существование этих граней для любых непустых конечных подмножеств.
Определение: Алгебра <L˄,˅> называется решёткой, если L- непустое множество, а ˄ и ˅- бинарные отношения операций на L, которые идемпотентны, коммутативны, ассоциативны и удовлетворяют двум тождествам поглощения.
Вспомогательные теоремы:
для того, чтобы доказать существование общей решётки для девяти элементов на множестве из пяти элментов, имеющих вернхнюю и нижнюю границу, выведем вспомогательные леммы, на которые будем опираться при преобразованиях выражений.
Лемма 1. (L1) Идемпотентность:a˄a=a; a˅a=a
Лемма 2. (L2) Коммутативность: a˄b=b˄a; a˅b=b˅a
Лемма 3. (L3) Ассоциативность: (a˄b)˄ c=a˄ (b˄c)
(a˅b) ˅ c=a˅ (b˅c)
Лемма 4. (L4) Тождества поглощения: a˄ (a˅b)=a , a˅ (a˄b=a)
Введение.
В первой половине девятнадцатого века попытка Джорджа Буля формализовать пропозициональную логику привела к понятию булевой алгебры. Исследуя аксиоматику булевых алгебр в конце девятнадцатого века, Чарльз Пирс и Эрнст Шрёдер сочли полезным ввести понятие решётки. Независимо от них, Ричард Дедекинд, в своих исследованиях по идеалам алгебраических чисел пришёл к тому же самому понятию. На самом деле Дедекинд ввёл также модулярность, ослабленную форму дистрибутивности. Хотя некоторые из ранних результатов этих математиков очень элегантны и нетривиальны, они не привлекли внимание математической общественностей.
И только работы Гаррета Биркгофа в середине 30-х годов дали толчок общему развитию теории решёток. В блестящей серии работ он продемонстрировал важность теории решёток и показал, что она является унифицирующим каркасом для доселе разрозненных достижений во многих математических дисциплинах. Сам Биркгоф, Валерий Иванович Гливенко, Карл Мингер, Джон фон Нейман, Ойстейн Оре и другие достаточно продвинулись в этой области, чтобы Биркгоф мог сделать попытку "подать" её широкой математической общественности, что он и сделал с удивительным успехом в первом издании своей монографии “Lеttice theory”.
Цель данной работы формулируется очень просто: доказать существование «самой общей решётки» для девяти элементов. На наш взгляд, дистрибутивные решётки сыграли многогранную роль в развитии теории решёток. Исторически теория решёток началась с (булевых) дистрибутивных решёток; в результате теория дистрибутивных решёток представляет одну из наиболее обширных и одну наиболее удовлетворительных глав теории решёток. Дистрибутивные решётки проясняют и обосновывают многие результаты общей теории решёток. Многие условия на решётки, а также элементы и идеалы решёток являются ослабленными формами дистрибутивности. Поэтому глубокое знание дистрибутивных решёток неоценимо при работе в теории решёток. Наконец, во многих приложениях на решётки, возникающие в различных областях математики, и особенно алгебры, налагается условие дистрибутивности.
Общий вид решётки из 5 элементов с условием сравнимости двух промежуточных элементов.
Будем использовать обозначения:
a![]() b=inf{a,b} a
b=inf{a,b} a![]() b=sup{a,b}
b=sup{a,b}
и будем называть «![]() »– пересечением, а «
»– пересечением, а «![]() »-объединением. В решётках они являются бинарными операциями, которые, будучи применены к паре элементов a,b
»-объединением. В решётках они являются бинарными операциями, которые, будучи применены к паре элементов a,b![]() L, снова дают элемент из L .
L, снова дают элемент из L .
Операции ![]() идемпотентны, коммутативны и ассоциативны, т.е обладают следующими свойствами:
идемпотентны, коммутативны и ассоциативны, т.е обладают следующими свойствами:
(L1) Идемпотентность:a˄a=a; a˅a=a
(L2) Коммутативность: a˄b=b˄a; a˅b=b˅a
(L3) Ассоциативность: (a˄b)˄ c=a˄ (b˄c)
(a˅b) ˅ c=a˅ (b˅c)
(L4) Тождества поглощения: a˄ (a˅b)=a , a˅ (a˄b=a)
Описание решёток:
Конечную решётку можно всегда описать с помощью таблицы пересечений и таблицы объединений.
Например: Пусть L={0,a,b,1}

Мы видим, что большая часть информации приведённой в таблицах, является лишней. Т.к обе операции коммутативны, то таблицы симметричны относительно главной диагонали. Более того, x˄x=x, x˅x=x, поэтому главные диагонали не несут в себе новой информации. Таким образом, две таблицы можно собрать в одну:
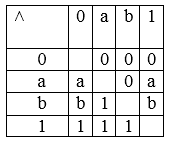
Другой способ описания решётки состоит в описании частичного порядка, т.е. множества всех таких <x,y>, что x![]() y.В предыдущем примере получаем:
y.В предыдущем примере получаем:
![]() ={(0,0),(0,a),(0,b),(0,1),(a,a),(a,1),(b,b),(b,1),(1,1)}
={(0,0),(0,a),(0,b),(0,1),(a,a),(a,1),(b,b),(b,1),(1,1)}
Очевидно, все пары вида (x,x) можно не включать в список, т.к. мы знаем, что x![]() x.Мы также знаем, что если x
x.Мы также знаем, что если x![]() y и y
y и y![]() z, то x
z, то x![]() z .Например, когда мы знаем, что 0
z .Например, когда мы знаем, что 0![]() a и a
a и a![]() 1,то нам не надо указывать, что 0
1,то нам не надо указывать, что 0![]() 1. Уточним нашу идею; будем говорить, что в частично упорядоченном множестве (P;
1. Уточним нашу идею; будем говорить, что в частично упорядоченном множестве (P; ![]() ) a покрывает b или b покрывается элементом a (и обозначать это так: a
) a покрывает b или b покрывается элементом a (и обозначать это так: a ![]() b или b
b или b![]() a ), если a>b и не существует x, такого, что a>x>b
a ), если a>b и не существует x, такого, что a>x>b
Отношение покрываемости в предыдущем примере имеет вид:
![]() ={(0,a),(o,b),(a,1),(b,1)}.
={(0,a),(o,b),(a,1),(b,1)}.
Диаграммы.
На диаграмме частично упорядоченного множества (P; ![]() ) элементы изображаются в виде маленьких кружков; кружки, соответствующие элементам x,y, соединяются прямой линией тогда и только тогда, когда один из них покрывает другой, если x покрывает y, то кружок соответствующий элементу x ,помещается выше кружка соответствующего элементу y [1].
) элементы изображаются в виде маленьких кружков; кружки, соответствующие элементам x,y, соединяются прямой линией тогда и только тогда, когда один из них покрывает другой, если x покрывает y, то кружок соответствующий элементу x ,помещается выше кружка соответствующего элементу y [1].
Постановка проблемы:
Пусть решётка имеет пять элементов 0,a,b,c,I и b<a, c![]() b=I, a
b=I, a![]() c=0.
c=0.
Покажем, что девять элементов
a,b, c, a˅c, b˅c, a˄c, b˄c, a˄ (b˅c), b˅(a˄c) образуют решётку. Изобразим общий её вид. Надо доказать, что из них при помощи операций объединения и пересечения мы не получим новых элементов. Мы должны проверить тридцать шесть объединений и тридцать шесть пересечений:
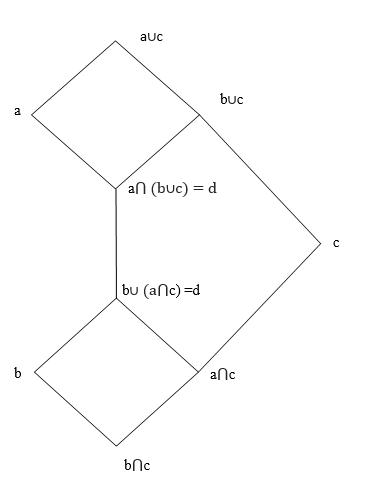
Рисунок 1. Диаграмма (общий вид) решётки для девяти элементов
Таблица 1.
Матрица для операции “˅”
|
|
a |
b |
c |
a˅c |
b˅c |
a˄c |
b˄c |
d |
t |
|
a |
--------- |
b |
a˅c |
a˅c |
a |
a˄c |
b˄c |
a |
a |
|
b |
b |
--------- |
b˅c |
a˅c |
b˅c |
D |
b |
d |
t |
|
c |
a˅c |
b˅c |
--------- |
a˅c |
b˅c |
C |
c |
b˅c |
b˅c |
|
a˅c |
a˅c |
a˅c |
a˅c |
--------- |
a˅c |
a˄c |
a˄c |
a˅c |
a˅c |
|
b˅c |
a |
b˅c |
b˅c |
a˅c |
--------- |
b˄c |
b˄c |
b˅c |
b˅c |
|
a˄c |
a˄c |
d |
c |
a˅c |
b˅c |
--------- |
a˄c |
d |
t |
|
b˄c |
b˄c |
b |
c |
a˅c |
b˅c |
a˄c |
--------- |
d |
t |
|
d |
a |
d |
b˅c |
a˅c |
b˅c |
D |
d |
--------- |
t |
|
t |
a |
t |
b˅c |
a˅c |
b˅c |
T |
t |
t |
--------- |
1) b˅a=a, ( т.к.a>b)
2) a˅b=a˅c (L2)
3) c˅b=b˅c (L2)
4) (a˅c) ˅a=a˅a˅c=a˅c (L2,L1)
5) (a˅c) ˅b=a˅b˅c=a˅c (L2,L1)
6) (a˅c) ˅c=a˅c (L2, т.к. a>b)
7) (b˅c) ˅a=b˅a˅c=a˅c (L2,L1)
8) (b˅c) ˅b=b˅b˅c=b˅c
9) (b˅c) ˅c=b˅c
10) (b˅c) ˅(a˅c)=b˅a˅c˅c=a˅c (L1,L4)
11) (a˄c) ˅a=a (L4)
12) (a˄c) ˅b=b˅ (a˄c) (L2)
13) (a˄c) ˅c=c (L4)
14) (a˄c) ˅a˅c=a˅c (L4,L2)
15) (a˄c) ˅ (b˅c)=(a˄c) (по свойствам дистрибутивности, L4)
16) a˅ (b˄c)= b˄c (L4)
17) (b˄c) ˅b=b (L4)
18) (b˄c) ˅c=c (L4)
19) (b˄c) ˅a˅c=(b˄c) ˅c˅a=a˅c (L2,L4)
20) (b˄c) ˅(b˅c)=b˅c (L4)
21) (b˄c) ˅(a˄c)= a˄c (L2)
22) b˅(a˄c) ˅a=a˅b˅(a˄c)a˅(a˄c)=a (т.к. a>b, L2,L4)
23) b˅(a˄c) ˅b=b˅b˅(a˄c)=b˅(a˄c) (L1,L2)
24) b˅(a˄c) ˅c=b˅c (L4)
25) b˅(a˄c) ˅a˅c=b˅a˅c˅(a˄c)=a˅c (т.к. a>b, L2,L4)
26) b˅(a˄c) ˅b˅c=b˅b˅c˅(a˄c)=b˅c (L1,L2)
27) b˅(a˄c) ˅(a˄c)=b˅(a˄c) (L1,L2)
28) b˅(a˄c) ˅(b˄c)=b˅(b˄c) ˅(a˄c)=b˅(a˄c) (L2,L4)
29) (a˄ (b˅c)) ˅a=a (L4)
30) (a˄ (b˅c)) ˅b=(b˅a) ˄ (b˅(b˅c))=a˄ (b˅c) (L1, т.к.a>b)
31) (a˄ (b˅c))˅c=(a˅c) ˄ (b˅c˅c)=(a˅c) ˄ (b˅c)=(a˅c)˄( c˅b)=b˅c(L2, L4)
32) (a˄ (b˅c)) ˅(a˅c)=a˅c (L4,по свойствам дистрибутивности)
33) (a˄ (b˅c)) ˅(b˅c)=b˅c (L4)
34) (a˄ (b˅c)) ˅(a˄c)= a˄ (b˅c) (L1,L2)
35) (a˄ (b˅c)) ˅( b˄c)= a˄ (b˅c) (L4)
36) (a˄ (b˅c)) ˅( b˅(a˄c))= b˅(a˄c) (L1,L2)
Таблица 2.
Матрица для операции “˄”
|
|
a |
b |
c |
a˅c |
b˅c |
a˄c |
b˄c |
d |
t |
|
a |
--------- |
b |
a˄c |
a |
a |
a˄c |
b˄c |
d |
t |
|
b |
b |
--------- |
b˄c |
b |
b |
b˅c |
b˄c |
b |
b |
|
c |
a˄c |
b˄c |
--------- |
c |
c |
a˄c |
b˄c |
a˄c |
a˄c |
|
a˅c |
a |
b |
c |
--------- |
b˅c |
a˄c |
b˄c |
d |
t |
|
b˅c |
a |
b |
c |
b˅c |
--------- |
a˄c |
b˄c |
d |
t |
|
a˄c |
a˄c |
b˄c |
a˄c |
a˄c |
a˄c |
--------- |
b˄c |
a˄c |
a˄c |
|
b˄c |
b˄c |
b˄c |
b˄c |
b˄c |
b˄c |
b˄c |
--------- |
b˄c |
b˄c |
|
d |
d |
b |
a˄c |
d |
d |
a˄c |
b˄c |
--------- |
d |
|
t |
t |
b |
a˄c |
t |
t |
a˄c |
b˄c |
d |
--------- |
1) a˄b=b(т.к a>b)
2) c˄a=a˄c (L2)
3) c˄b=b˄c(L2)
4) (a˅c)˄a=a (L4)
5) (a˅c)˄b=(a˄b) ˅(c˄b)=b˅(c˄b)=b (т.к a>b , L4)
6) (a˅c)˄c=c(L4 )
7) (b˅c)˄a=a˄(b˅c) (L2)
8) (b˅c)˄b=b (L4)
9) (b˅c)˄c=c (L4)
10) (b˅c)˄(a˅c)=((b˅c)˄a) ˅((b˅c)˄c)=((b˅c)˄a) ˅c=b˄a˅(c˄a) ˅c=b˅c( т.к a > b, L4, по свойствам дистрибутивности)
11) (a˄с)˄a=a˄a˄c=a˄c (L2,L1)
12) (a˄c)˄b=a˄b˄c=b˄c (т.к a>b, L2)
13) (a˄c)˄c= a˄c (L1)
14) (a˄c) ˄(a˅c)=(a˄c˄a) ˅(a˄c˄c)=(a˄c) ˅(a˄c)=a˄c (L1)
15) (a˄c)˄(b˅c)=a˄c
16) (b˄c)˄a=b˄a˄c=b˄c (т.к a>b, L2)
17) (b˄c)˄b=b˄b˄c=b˄c (L2, L1)
18) (b˄c)˄=b˄c (L1)
19) (b˄c)˄(a˅c)=(b˄c˄a) ˅(b˄c˄c)=(b˄c) ˅(b˄c)=b˄c (по свойствам дистрибутивности)
20) (b˄c)˄(b˅c)=(b˄c˄b) ˅(b˄c˄c)=(b˄c) ˅(b˄c)= b˄c (по свойствам дистрибутивности и L1)
21) (b˄c)˄(a˄c)=b˄a˄c˄c=b˄c (L2, т.к a>b, L1)
22) (b˅(a˄c))˄a=((a˄c) ˅(b˄a)=(a˄c) ˅b (L2, т.к a>b)
23) (b˅(a˄c))˄b=b (L4)
24) (b˅(a˄c))˄c=a˄c (L4, по свойствам дистрибутивности)
25) (b˅(a˄c))˄(a˅c)=b˅(a˄c) (L4)
26) (b˅(a˄c))˄(b˅c)=(b˅c)˄b˅(a˄c˄b˄c)=b˅(a˄b˄c˄c)=b˅(a˄c) (т.к a>b, L1)
27) (b˅(a˄c))˄(a˄c) =a˄c (L4)
28) (b˅(a˄c))˄(b˄c)=(b˄c˄c) ˅(a˄b˄b˄c)=(b˄c) ˅(b˄b˄c)=(b˄c) ˅(b˄c)=b˄c (L2,L1, т.к a>b)
29) (a˄(b˅c))˄a=a˄a˄(b˅c)=a˄(b˅c) (L1, L2 по свойствам дистрибутивности)
30) (a˄b(b˅c))˄b=a˄b˄(b˅c)=b˄(b˅c)=b (т.к a>b , L4)
31) (a˄(b˅c))˄c=((a˄c)˄)b˅c=a˄c (L4)
32) (a˄(b˅c))˄(a˅c)=a˄(a˅c)˄(b˅c)=a˄(b˅c) (L2, L4)
33) (a˄(b˅c))˄(b˅c)= a˄(b˅c) (L1)
34) (a˄(b˅c))˄(a˄c)=a˄a˄c(b˅c)=a˄c (L1, L2, L4)
35) (a˄(b˅c))˄(b˄c)= a˄b˄c=b˄c (т.к a>b, L4)
36) (a˄(b˅c))˄(b˅(a˄c))=(a˄(b˅c)˄b) ˅ ˅(a˄(a˄c)˄(b˅c)=(a˄b)˅(a˄c)=b˅(a˄c) (т.к a>b, L4,L1)
Заключение/
Проведя алгебраические преобразования и составив по результатам матрицы, мы пришли к выводу, что возможно построение общей решётки для девяти элементов, т.к. новых элементов получено не было. Тем самым доказательство теории решёток для данных условий на девяти элементах a,b, c, a˅c, b˅c, a˄c, b˄c, a˄ (b˅c), b˅(a˄c), при условии что b<a и аксиом теории решётки верно.





