МОДИФИКАЦИЯ АЛГОРИТМОВ ВЫДЕЛЕНИЯ СОЦИАЛЬНЫХ СООБЩЕСТВ НА ОСНОВЕ ИНФОРМАЦИОННОГО СОДЕРЖАНИЯ

В настоящее время социальные сети становятся все более популярными. При этом увеличивается не только число пользователей в одной социальной сети, но и увеличивается число самих социальных сетей. В связи с этим возникает огромное множество актуальных и интересных для исследования задач, связанных со структурированием, обработкой и анализом информации, содержащейся в социальных сетях. Решение одной из таких задач, а именно задачи метрической кластеризации выделения сообществ в социальных сетях, – предмет данной статьи.

Анализ социальных сетей – это направление, которое занимается описанием и анализом социальных сетей посредством различных методов, в том числе с помощью теории графов. Одной из основных задач анализа социальных сетей является определение групповых структур сетей (сообществ). Сообщество, или кластер – это набор вершин, относительно сильно связанных друг с другом, и, возможно, обладающих общими свойствами или играющих схожие роли в сети. Знания о структуре сообществ незаменимы для предсказания связей и атрибутов пользователей, расчёта близости пользователей в социальном графе, оптимизации потоков данных в социальной сети, некоторых аналитических приложений и т.д. Существует множество критериев для графа, которые показывают некоторую его качественную характеристику. Широко используемым критерием для обнаружения сообщества является модулярность. Модулярность - это скалярная величина из отрезка [−1, 1], которая количественно описывает неформальное определение структуры сообществ:

,

где: m - количество связей,  - матрица смежности графа, k_i - степень вершины

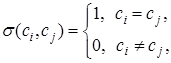
c_i - номер класса, к которому принадлежит вершина i.

Задача поиска выделения сообществ в графе сводится к поиску таких с_i, которые максимизируют значение модулярности. Достоинства модулярности заключаются в том, что она достаточно просто интерпретируется. Ее значение равно разности между долей ребер внутри сообщества и ожидаемой доли связей, если бы ребра были размещены случайно. Модулярность возможно эффективно пересчитывать при небольших изменениях в кластерах.

Обработка социальных данных требует также разработки соответствующих алгоритмических и инфраструктурных решений, позволяющих учитывать их размерность. К примеру, граф социальной сети Facebook на сегодняшний день содержит более 1 миллиарда пользовательских аккаунтов и более 100 миллиардов связей между ними. Каждый день пользователи добавляют более 200 миллионов фотографий и оставляют более 2 миллиардов комментариев к различным объектам сети. На сегодняшний день большинство существующих алгоритмов, позволяющих эффективно решать актуальные задачи, не способны обрабатывать данные подобной размерности за приемлемое время [2,5–10]. В связи с этим, возникает потребность в новых решениях, позволяющих осуществлять распределённую обработку и хранение данных без существенной потери качества результатов.

 В данной статье рассмотрим метод, с помощью которого можно эффективно выделять сообщества в сети, базируясь на модификации алгоритмов для нахождения сообществ [3]. Общую схему работы алгоритма выделения сообществ можно представить следующим образом.

Изначально каждая вершина считается отдельным сообществом. Вычисляется целевая функция L(M)

                                ,                                       (1)  

где: 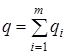 - вероятность перехода между сообществами на каждом шаге случайного блуждания, q_i - вероятность покинуть сообщество i, p_α - вероятность посетить вершину α,  - вероятность остаться в сообществе i. Энтропию переходов между сообществами, определяемую как нижняя граница средней длины кодового слова для именования сообществ, представим в виде

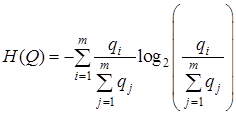                               ,                                     (2)

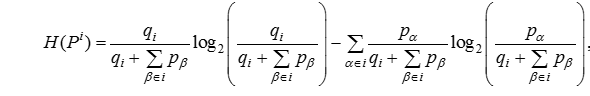(3)

 - энтропия перемещения внутри сообщества i, нижняя граница средней длины кодового слова для именования вершин в сообществе i. Тогда более детальное описание метрики L(M) можно представить в виде

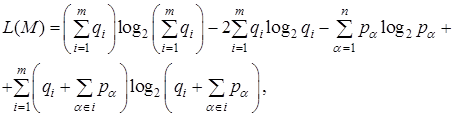                          (4)

где: 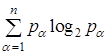 не зависит от разбиения сети на сообщества. Поэтому, при оптимизации разбиения сети, необходимо учитывать все изменения:  — вероятность, с которой случайное блуждание входит и выходит из сообществ, и  — долю времени, которую случайное блуждание проводит в каждом из

сообществ.

Далее случайное блуждание формирует последовательность вершин. С учётом частоты встречаемости вершин в полученной последовательности выбираются подмножества вершин, которые объединяются в сообщества. Для заданного разбиения вычисляется метрика L(M). Если её значение стало меньше, то разбиение M сохраняется и продолжается работа алгоритма. Иначе, если значение целевой функции L(M) не уменьшилось, то полученное разбиение M можно считать результатом выделения сообществ в сети.

Рассмотрим модификацию метода для неориентированных взвешенных сетей[3]. Введём относительный вес вершины α

                                                   ,                                               (5)

где: l_α - множество инцидентных связей вершины α, w_l - вес связи l. Тогда с учётом (5) задается относительный вес сообщества i

.

Пусть  - вес выхода из сообщества i

,

где: - множество связей, выходящих из сообщества i.

Общий вес связей, соединяющих сообщества

.

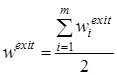При использовании неориентированных взвешенных сетей метрика качества разбиения L(M) будет выглядеть следующим образом:

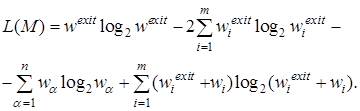                                             (6)

На основе рассмотренного численного алгоритма решения задачи выделения сообществ в социальных сетях для неориентированных взвешенных сетей разработан программный продукт на языке C# программной среды Microsoft Visual Studio.

Данные взяты из социальной сети ≪ВКонтакте≫ (vk.com) . Для примера будем рассматривать 345 случайных вершин. Вершины - это профили социальной сети, а связи - отношения дружбы между ними. На рисунке 1 слева расположены вершины сети, размещённые случайным образом, справа приведены размещения по результатам работы алгоритма.

Благодаря проведённым исследованиям эмпирических данных социальной сети ≪ВКонтакте≫ стало возможным составить следующий список свойств сообществ пользователей на уровне связей между пользователями в социальном графе:

·     вершины в сообществе более тесно связаны друг с другом, чем с вершинами за пределами сообщества;

·     сообщества могут пересекаться, т.е. один пользователь может относиться к нескольким сообществам, что хорошо согласуется с тем фактом, что человек одновременно может играть несколько социальных ролей в обществе;

·     вершины с небольшой степенью чаще входят в небольшое число сообществ, тогда как вершины с большой степенью входят во множество сообществ.

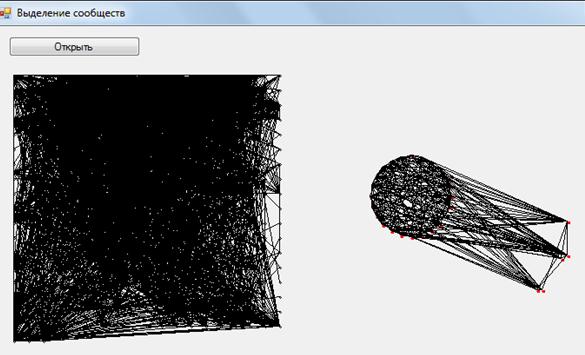
Рисунок 1. Выделение сообществ в социальных сетях. Количество вершин – 345

Результатом работы метода поиска сообществ является множество сообществ, в котором каждая вершина принадлежит как минимум одному сообществу.

В ходе исследования задачи кластеризации социальных сообществ на основе информационного содержания преобразован алгоритм выделения сообществ, который показывает возможность эффективного применения предложенной модификации к большим данным реальных социальных сетей.