ИССЛЕДОВАНИЕ АЛГОРИТМА БЕРЛЕКЭМПА-МЕССИ, ПРЕДНАЗНАЧЕННОГО ДЛЯ ДЕКОДИРОВАНИЯ БЧХ КОДОВ, И ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ КОДЕКА В СИСТЕМЕ MATHCAD

В работе [1] авторами были исследованы и практически реализованы в среде MathCAD два из трех метода декодирования БЧХ кодов. Это были метод прямого решения – алгоритм Питерсона-Горинштейна-Цирлера и евклидов алгоритм. Данная работа является продолжением и логическим завершением исследования подкласса циклических кодов – кодов БЧХ (Боуза-Чоудхури-Хоквенгема), исправляющих большое число ошибок в блоке данных.

Отметим, что в современное время в связи с бурным развитием беспроводных технологий (bluetooth, NFC, Wi-Fi, WiMAX, мобильные сети и т.д.), была и остается одной из актуальных проблем передачи достоверная доставка пользовательской и служебной информации. Одним из основных средств обеспечения высокой помехоустойчивости при транспортировке информации является корректирующее кодирование. Методы обнаружения и исправления ошибок основаны на передаче в составе блока данных избыточной служебной информации, по которой можно судить с некоторой степенью вероятности о достоверности принятых данных [3].

Циклические коды составляют класс кодов, исправляющих ошибки, кодирование и декодирование которых основано на полиномиальном представлении. Взять к примеру современную технологию Ethernet. В поле контрольной суммы кадра используется образующий полином циклического кода CRC-32   Простая реализация этих кодов использует регистры сдвига и логические схемы [2].

Коды БЧХ составляют мощный класс циклических кодов, которые обеспечивают достаточную свободу выбора длины блока, степени кодирования, размеров алфавита и возможностей коррекции ошибок [3].

Исследовались именно двоичные БЧХ коды, так как они имели широко распространение в компьютерных сетях и устройствах памяти из-за простого и быстрого кодирования и декодирования. Кроме того, укороченные (48,36,5) БЧХ коды использованы в Американской сотовой системе с временным разделением каналов (TDMA, стандарт IS-54). [2]

Перейдем непосредственно к рассмотрению основного вопроса, касающегося весьма эффективного алгоритма Берлекэмпа-Месси (BMA). Напомню, что ключевой задачей декодирования БЧХ кодов (двоичных и недвоичных) является решение ключевого уравнения 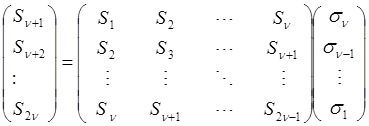(1):

 ,                         (1)

устанавливающего связь между коэффициентами полинома локаторов ошибок  и синдромами . Решение ключевого уравнения требует довольно интенсивных вычислений в процедуре декодирования БЧХ кодов [2]. Алгоритм BMA является как раз одним из таких методов. По числу операций в конечном поле этот алгоритм обладает высокой эффективностью. BMA обычно используется для программной реализации или моделирования кодов БЧХ и кодов Рида-Соломона.

Напомню, что теория декодирования при исправлении ошибок базируется на арифметике полей Галуа. Они называются конечными, подразумевая конечное число принадлежащих ему элементов. Вычисления в полях Галуа позволяют заменить сложные комбинационные схемы практичными процессорными архитектурами [2].

BMA лучше рассматривать как итеративный процесс построения минимального линейного регистра (сдвига) с обратной линейной связью (ЛРОС), который генерирует последовательность синдромов

В работе [1] авторами был рассмотрен и реализован прямой метод решения ключевого уравнения. Алгоритм PGZ – лучший путь к пониманию декодирования кодов БЧХ. Но нельзя забывать о степени эффективности разных методов. Прямое решение требует обращение матрицы размером (исправляющая способность кода). Хоть данная процедура не приводит к ошибкам округления в конечном поле, вычислительная работа при достаточно больших t может оказаться чрезмерно большой. С проблематикой вычислительной мощности при больших t справляется BMA.

Целью BMA является построение многочлена обратной связи  наименьшей степени (рис. 1), удовлетворяющего следующему уравнению, выведенному из (1):

                                  (2)

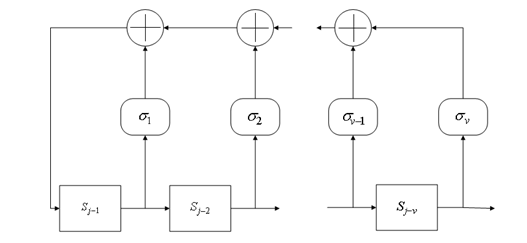
Рисунок 1. ЛРОС

Решение этой задачи будет эквивалентно решению условию, что многочлен

                     (3)

является многочленом обратной связи ЛРОС, который генерирует ограниченную последовательность синдромов.

На каждой итерации вычислений необходимо рассчитывать несовместность (рассогласование, расхождение, различие), определенная как

                          (4)

и являющаяся мерой соответствия синдромной последовательности и генерируемой ЛРОС. Возможны два случая: когда  и когда  В зависимости от этого алгоритм будет выполняться по разному.

В начале алгоритма задаются начальные условия для выполнения необходимых действия на последующих итерациях.

В разных источниках можно видеть разные схемы данного алгоритма декодера, но суть от этого не меняется. Для наглядности воспользуемся блок-схемой [6]:

Рисунок 2. Блок-схема алгоритма Берлекэмпа-Месси

Задавая начальные условия декодеру, мы таким образом инициализируем его работу и начало итеративного процесса. В зависимости от вычисленной несовместности декодер будет строить регистр минимальной длины и на выходе мы получим многочлен наименьшей степени, который и будет полиномом локаторов ошибок. Если вычислительный процесс будет длиться больше итераций, чем исправляющая способность кода, и в результате не выполнятся условия остановки алгоритма, декодер выдаст сигнал о превышении допустимого количества ошибок в блоке данных.

Для практической реализации кодеков была выбрана система алгебраического проектирования MathCAD v.15. Были реализованы два кода двоичных БЧХ кодов: (15.5.7), исправляющий 3 и меньше ошибок, и (15.7.5), исправляющий все одно- и двукратные ошибки.

Соответственно для корректной работы кодеков и выполнения всех функций алгоритма были созданы подпрограммы-функции, позволяющие работать в поле Галуа , осуществлять все необходимые операции с элементами поля, а также функции для вычисления синдромов, нахождения корней полинома локаторов ошибок и обращения их [1]. Конкретно для данного алгоритма были созданы функции для вычисления различия , которое требует строго правильного определения многочлена обратной связи и длины регистра на каждой итерации, а также функции проверки декодера на исправление всевозможных ошибок. Они работает по принципу создания всех возможных векторов ошибок в матрице. Затем подставляя поочередно все векторы, проверяет, исправляет ли декодер принятую комбинацию, ассоциированную с таким вектором ошибок. В результате выводится сообщение об успешном исправлении в случае положительного результата.

Проанализировав все этапы алгоритма, автором было подтверждено, что на нечетных шагах [2].Для двоичных БЧХ это закономерность. Таким образом можно выполнять только четные шаги алгоритма, изменив при этом правило остановки алгоритма, в результате чего должна снизиться сложность декодирования и увеличиться скорость итеративного вычисления.

Список литературы:

1. Зиновьев П. А., Пражак В. И., Сравнение двух методов декодирования БЧХ кодов, их практическая реализация в MathCAD, Электронный сборник статей по материалам ХХI студенческой международной заочной научно-практической конференции. — Москва: Изд. «МЦНО». — 2015. — № 2 (21) / [Электронный ресурс] — Режим доступа. — URL: http://www.nauchforum.ru/archive/MNF_tech/2(21).pdf (Дата обращения 15.01.16).
2. Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. Москва: Техносфера, 2005. – 320с.
3. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. - М.: Издательский дом «Вильнюс», 2003. - 1104 с.: ил. - Парал. тит. англ.
4. Олифер В.Г., Олифер Н.А. Компьютерные сети. принципы, технологии, протоколы: Учебник для вузов. 3-е изд. - СПб.: Питер, 2007.- 958с.: ил.
5. Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. – М.: Мир, 1986. – 576с. – ил.
6. Алгоритм Берлекэмпа-Месси – [Электронный ресурс] — Режим доступа. — URL: https://ru.wikipedia.org/wiki/Алгоритм_Берлекэмпа_—_Мэсси (Дата обращения 02.02.16).