ПРИМЕНЕНИЕ МЕТОДИК МАТЕМАТИЧЕСКОГО ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОПТИМИЗАЦИИ ПАРАМЕТРОВ ДИФФУЗИОННОЙ СВАРКИ ТВЁРДЫХ СПЛАВОВ СО СТАЛЯМИ
Секция: 8. Машиностроение

XXIX Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
ПРИМЕНЕНИЕ МЕТОДИК МАТЕМАТИЧЕСКОГО ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ ДЛЯ ОПТИМИЗАЦИИ ПАРАМЕТРОВ ДИФФУЗИОННОЙ СВАРКИ ТВЁРДЫХ СПЛАВОВ СО СТАЛЯМИ
В данной работе для оптимизации параметров диффузионной сварки твердых сплавов со сталями (на примере сплава ВК-15 и стали 45) использовали методики математического планирования экспериментов. В этих методиках задачи со многими факторами эксперимента ставятся так, чтобы варьировать все факторы сразу и оценивать каждый эффект по всей совокупности опытов, что дает возможность значительно сократить их количество и получить более достоверные представления.
Важным преимуществом многофакторного эксперимента также является то, что исследуемые параметры могут быть определены с меньшей ошибкой, чем при однофакторном методе.
Изложенное позволяет сделать заключение о целесообразности использования принципа многофакторного эксперимента в исследованиях по отысканию оптимальных параметров в режимах процесса ДСВ различных сочетаний материалов, в том числе и стали с твердым сплавом. Его реализация предусматривает проведение следующих этапов:
· Постановка задачи, выбор зависимых переменных (откликов), выбор независимых переменных (факторов) и уровень варьирования для них.
· Выбор математической модели для описания процесса.
· Порядок проведения экспериментов, интерпретация результатов и практические выводы.
Основным критерием качества соединений, полученных пайкой и сваркой, являются их механические характеристики: предел прочности на разрыв (отрыв), на срез (сдвиг), ударная вязкость. В то же время, с приложением сжимающих усилий, в результате пластической деформации наблюдается некоторое увеличение размеров деталей в приконтактной зоне. Деформация деталей при их соединении выше назначаемых допусков приводит к необходимости последующей механической обработки, а при невозможности таковой – браку продукции.
В связи с этим была поставлена задача отыскать оптимальные режимы процесса, которые позволили бы получить диффузионное соединение твердого сплава со сталью, обладающее высокой прочностью с минимальной пластической деформацией стального образца в приконтактной зоне.
С учетом этого, в данном случае, целесообразно отклик (выход) представить в виде двух зависимых переменных:
У1 – прочность соединения на отрыв Qотр в Н;
У2 – деформация стального образца ε %.
При построении математической модели системы обычно стремятся к самому простому ее виду; в то же время она должна наиболее правдоподобно отражать существенные стороны исследуемой системы. В этой связи целесообразно ограничивать число факторов, включая в математическую модель только те из них, которые оказывают первостепенное влияние на ход процесса.
Проведенные предварительные эксперименты по диффузионному соединению стали с твердым сплавом позволили выбрать целесообразный способ подготовки поверхностей к сварке. Шлифовка поверхностей с Ra=3.2–1.6 мкм с последующим обезжириванием, обеспечивает при сварке в рабочем вакууме получение соединения достаточно высокой твердости.
В этой связи в качестве варьируемых переменных были выбраны следующие параметры – температура процесса, удельное давление сжатия и время изотермической выдержки. Поэтому для исследования в план проведения эксперимента были включены следующие независимые переменные:
Х1 – температура процесса, Т0С;
Х2 – удельное давление сжатия, Р [МПа];
Х3 – время изотермической выдержки, τ [мин].
Остальные параметры исследуемого процесса фиксировались на постоянном уровне. Так, степень разряжения в камере составляла 10-4 –5 ·10-5 мм рт. ст., поверхность образцов готовилась согласно принятой методике, в качестве промежуточной прослойки был применен химически осажденный никель постоянной толщины в 25–30 мкм.
Важное значение при подготовке эксперимента имеет правильный выбор границ интервала варьирования независимыми переменными. Независимые переменные должны варьироваться в диапазоне, отражающем наиболее характерные особенности изучаемого процесса, а результаты – иметь познавательную практическую ценность.
С учетом этих соображений, а также на основании анализа априорной информации об исследуемом процессе были выбраны следующие границы варьирования независимых переменных:
Х1 – от 7000С до 11000С;
Х2 – от 5 МПа до 20 МПа;
Х3 – от 5 мин. до 20 мин.
В практическом отношении для решения задач при поиске оптимальных условий проведения технологических процессов и в планировании эксперимента целесообразной моделью можно считать локально-интегральную (полиноминальную) модель.
Исходя из этого уравнение регрессии в общем виде может быть представлено выражением:
![]() , (1)
, (1)
где: В0, Вi, Bij, Bii … – коэффициенты регрессии;
К – количество независимых переменных.
Область варьирования переменных (таблица 1) выбирается таким образом, чтобы она охватывала реально возможные изменения параметров режима ДСВ исследуемого сочетания материалов.
Таблица 1.
Уровни варьирования переменных
Переменная |
Основной уровень (0) |
Интервал варьирования |
Верхний уровень (+1) |
Нижний уровень (-1) |
Х1 |
900 |
200 |
1100 |
700 |
Х2 |
1,25 |
0,75 |
2 |
0,5 |
Х3 |
12,5 |
7,5 |
20 |
5 |
В данной работе опуская рассмотрение математической модели с полиномом более низкого порядка, строилась математическая модель с полиномом высокого порядка. В этом случае строится план многофакторного эксперимента второго порядка для К= 3 (табл. 3.2) и в соответствии с этим планом были проведены эксперименты.
Определение коэффициентов регрессии сводится к вычислению сумм (Оу), (iy ), (ijy) и (iiy):
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
где: 
Вычисленные на ЭВМ по этим формулам коэффициенты регрессии были проверены на значимость, а полученные уравнения – на адекватность.
Таблица 2.
Планирование второго порядка
№ |
Матрица планирования |
Результаты опытов |
|||
X1 |
X2 |
X3 |
Qотр,H |
ε % |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
-1 1 -1 1 -1 1 -1 1 -1,682 1,682 0 0 0 0 0 0 0 0 0 0 |
-1 -1 1 1 -1 -1 1 1 0 0 -1,682 1,682 0 0 0 0 0 0 0 0 |
-1 -1 -1 -1 1 1 1 1 0 0 0 0 -1,682 1,682 0 0 0 0 0 0 |
15700 53200 24400 60800 27400 57200 18300 67600 10100 65800 36400 53700 43100 52600 48700 50200 48800 49100 49000 50600 |
0,04 0,06 0,09 2,60 0,06 0,80 0,11 4,10 0,06 4,60 0,01 1,00 0,02 0,30 0,225 0,215 0,200 0,205 0,210 0,230 |
Статистический анализ показал, что уравнение второго порядка с достоверной точностью описывает зависимость изменения прочности соединения (У1) от исследуемых параметров процесса (х1 , х2 , х3). Однако второе уравнение, моделирующее зависимость изменения деформации образца (У2) от этих же параметров, оказалось неадекватным. Так как стандартных схем планирования третьего порядка в настоящее время не существует, то в таких ситуациях используются специальные приемы. В данном случае применен принцип наименьших квадратов. С помощью этого метода можно вычислить уравнение регрессии заданного порядка. Для этого вначале составляется сумма
S = ∑ [Уi – f (хi)]2 , (6)
где: функция f (хi) записана со всеми неопределенными коэффициентами a,b,c и т. д. Задача состоит в том, чтобы найти набор коэффициентов a,b,c …, минимизирующих величину S.
Для нахождения коэффициентов составлялась система нормальных уравнений, число которых в системе равно количеству определяемых коэффициентов.
Полученная линейная система уравнений достаточно сложна (восемь уравнений). Решение ее проводилось с помощью ЭВМ итерационным методом (так как процедура вычисления коэффициентов регрессии громоздка и не представляет познавательного интереса, а является только вспомогательной, она в работе не приводится). Полученные коэффициенты проверялись на значимость в пределах доверительных групп, а полученное уравнение третьего порядка – на адекватность.
Проведённый статистический анализ показал, что оба уравнения регрессии вида
![]() (7)
(7)
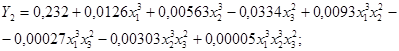 (8)
(8)
адекватно описывает процесс диффузионного соединения твердого сплава со сталью и могут служить его моделью.
Условные переменные х1, х2, х3 связаны с натуральными переменными Х1, Х2 , Х3 зависимостями переходного вида:
![]() (9)
(9)
где: Х0i – основной уровень i –й переменной; ΔХi – интервал варьирования i – й переменной.
Применяя эту формулу к нашим варьируемым переменным получаем:
![]()
![]() (10)
(10)
![]()
Полученная математическая модель адекватно описывает процесс ДСВ твердых сплавов со сталями. Для подтверждения результатов анализа и наглядности была произведена экспериментальная проверка расчетных значений параметров. С этой целью (рисунок 1 (а, б, в)) построена графическая зависимость прочности соединения -σß и деформации образца – ε % от трех исследуемых параметров режима в пределах выбранной области их варьирования и при последовательном фиксировании двух из них на определенном уровне. На эти графики накладывались кривые, полученные экспериментальным путем с использованием тех же табличных данных параметров режима.
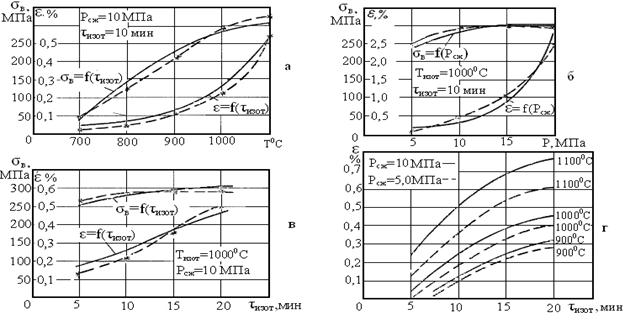
Рисунок 1. Сравнение расчётных и экспериментальных параметров процесса
Как можно видеть из рисунка 1 (а, б, в), характер изменения кривых, описанных моделью (сплошная линия), идентичен экспериментальным (штриховая линия); при этом имеющаяся разница значений в соответствующих точках не превышает величины ошибки эксперимента. Таким образом, экспериментальная проверка также подтверждает приемлемость полученной модели для описания и исследования процесса ДСВ твердых сплавов со сталями.
Таким образом, полученная математическая модель, ее расчетные и графические выражения позволяют с достаточной ясностью и достоверностью представить особенности процесса ДСВ твердых сплавов со сталями и им подобным сочетаниям. Анализ результатов исследования модели дает возможность не только выбрать оптимальный режим диффузионного соединения для конкретного сочетания, но и с большей обоснованностью подходить к вопросам конструирования твердосплавного штампового инструмента.
Полученные кривые могут быть использованы для оценки области оптимальных режимов диффузионной сварки исследуемого сочетания материалов, вместе с тем, в практике не удобны.
В связи с этим, с целью обеспечения быстрого поиска оптимальных параметров процесса, на основании анализа ЭВМ, была построена номограмма (рисунок 2). По этой номограмме определены оптимальные параметры режима сварки при прочности соединения 312,5 МПа:
температура процесса Т = 10250С,
удельное давление сжатия Р = 10.9 МПа,
время изотермической выдержки τ = 18 мин.

Рисунок 2. Номограмма для определения параметров режима диффузионной сварки в вакууме твердого сплава ВК-15 и стали 45 в зависимости от прогнозируемой прочности соединения
Таким образом, в результате проведённых исследований получены данные, составляющие основу технологии диффузионной сварки твёрдого сплава ВК-15 со сталью 45. Результаты работы могут найти применение в инструментальной промышленности- при изготовлении режущего и штампового инструментов, а также изделий нового назначения.
Список литературы:
- Бондарь А.В., Пешков В.В., Киреев Л.С., Шурупов В.В. Диффузионная сварка титана и его сплавов / Под ред. А.В. Бондаря. – Воронеж: Воронежский государственный университет, 1998. – 265 с.
- Люшинский А.В. Диффузионная сварка разнородных материалов: учеб. пособие для студ. высш. учеб. заведений / Под ред. А.В. Люшинского. – М.: Издательский центр «Академия», 2006. – 208 с.
- Спирин Н.А., Лавров В.В. Методы планирования и обработки результатов инженерного эксперимента: Конспект лекций / Под ред. Н.А. Спирина. – Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2004. – 257 с.





