УРАВНЕНИЕ БЮРГЕРСА И ЕГО ДИСКРЕТИЗАЦИИ

Уравнение Бюргерса для вещественнозначной функции  записывается в следующем виде:

Здесь параметр  представляет собой вязкость. Начальные данные для этого уравнения задаются следующим образом:

Различные свойства решений уравнения Бюргерса установлены в работах [1; 2; 7; 8; 9].

В работе [1] устанавливаются аналитические свойства решений уравнения Бюргерса в периодическом по пространственной переменной случае. Практически важным представляется разработка численных методов, позволяющих получить аналогичные результаты численными методами. Это связано с тем, что численные методы могут быть применимы даже когда аналитические методы не работают. В данной работе, следуя [1] и [6], будем считать, что начальные данные и само решение являются периодическими, с периодом L:

Для того, чтобы можно было произвести численный расчет решения уравнения, мы произведем дискретизацию пространственной переменной x в количестве N узлов. Иными словами, мы рассмотрим N функций  для . Дискретизацию выражений  и  будем производить согласно следующим формулам:

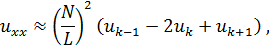
Точность этих приближений составляет , где . Подставив в исходное уравнение Бюргерса, мы приходим к системе «зацепленных» обыкновенных дифференциальных уравнений первого порядка на набор функций , зависящих от t:

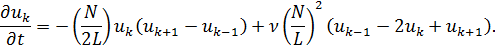
Далее мы можем произвести масштабирование или калибровку, чтобы «избавиться» от параметров. Например, это можно сделать посредством следующей замены:

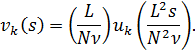
Эта и подобные нормировки обеспечивают переход к безразмерным величинам (время, расстояние и скорость) и обычно применяются для приведения уравнений к каноническому виду.

В нашем случае, дискретизация уравнения Бюргерса принимает следующий вид:

                                (1)

Мы получили систему из N «зацепленных» обыкновенных дифференциальных уравнений, по одному уравнению для каждой величины , где индекс  меняется в следующих пределах: . Отметим, что зацепления являются квадратическими. Периодические краевые условия означают, что

Отметим, что дискретизация (1) сохраняет полное количество движения (или импульс тела) в том смысле, что выполнено следующее соотношение:

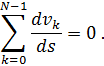
Это свойство согласуется с законом сохранения полного количества движения для исходного уравнения Бюргерса, которое заключается в следующем. Для каждого конкретного решения  уравнения Бюргерса числовое значение количества движения не зависит от времени:

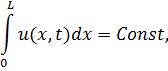
но может зависеть от выбора системы координат. Числовое значение константы можно поменять, сделав преобразование Галилея:

Следовательно, не умаляя общности, мы можем считать, что полное количество движения равно нулю. Значит, в случае рассматриваемой дискретизации имеет смысл делать следующее предположение:

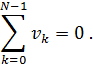
Это ограничение на сумму окажется очень удобным впоследствии.

Кинетическая энергия, с другой стороны, не сохраняется дискретизацией (1), даже если отбросить диссипативные (линейные) члены (диссипативные члены отсутствуют в случае, когда вязкость , но и нормализация дискретизации выглядит немного иначе). Это происходит потому, что в общем случае

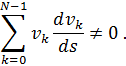
В случае уравнения Бюргерса для кинетической энергии поля скоростей , которая в момент времени t задается следующим интегралом:

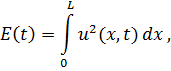
выполнено соотношение:

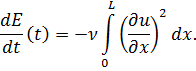
Как следствие, кинетическая энергия убывает, кроме случаев, когда поле скоростей постоянно по x и/или вязкость . Поэтому решения дискретизированной системы (1), для которых кинетическая энергия неограниченно возрастает, либо решения, которые постоянны во времени, но не по x, должны быть классифицированы как «особенности» или «ложные» решения дискретизации (1). С подобными «ложными» решениями можно познакомиться в работе [6]. Отметим, что некоторой альтернативой к методу дискретизации является метод точечных потенциалов, который может быть применен к уравнению Россби, с которым можно познакомиться в работах [3; 4; 5].

Список литературы:

1. Бирюк А.Э. Спектральные свойства решений уравнения Бюргерса с малой диссипацией // Функциональный анализ и его приложения. – 2001. – Т. 35. – № 1. – С. 1–15.
2. Бирюк А.Э. Преобразование уравнения Бюргерса // В книге: Функциональные пространства. Дифференциальные операторы. Общая топология. Проблемы математического образования тезисы докладов 4-ой Международной конференции, посвященной 90-летию со дня рождения члена-корреспондента РАН, академика Европейской академии наук Л.Д. Кудрявцева. – 2013. – С. 646–647.
3. Свидлов А.А. Вихревое обтекание острова в канале // Экологический вестник научных центров Черноморского экономического сотрудничества. – 2006. – Спец. выпуск. – С. 141–143.
4. Свидлов А.А., Бирюк А.Э., Дроботенко М.И. Негладкое решение уравнения Россби // Экологический вестник научных центров Черноморского экономического сотрудничества. – 2013. – № 2. – С. 89–94.
5. Свидлов А.А., Дроботенко М.И., Бирюк А.Э. Множество единственности потенциала простого слоя // Экологический вестник научных центров Черноморского экономического сотрудничества. – 2015. – № 2. – С. 77–81.
6. Aref Н., Daripa P.K., Note on finite difference approximations to Burgers’ equation // SIAM J. Sci. Stat. Comput. – 1984 – Vol. 5, – № 4, – Р. 856–864.
7. Biryuk A. On generalized equations of Burgers type with small viscosity // В книге: Международная конференция «Дифференциальные уравнения и смежные вопросы», посвященная 100-летию со дня рождения И.Г. Петровского XX сессия совместных заседаний Московского математического общества и семинара им. И.Г. Петровского. Тезисы докладов. – 2001. – С. 60–61.
8. Biryuk A. Note on the transformation that reduces the Burgers equation to the heat equation // preprint – 2003. – mp_arc:03-370.
9. Biryuk A. On multidimensional Burgers type equations with small viscosity // В сборнике: Contributions to Current Challenges in Mathematical Fluid Mechanics Сер. “Advances in Mathematical Fluid Mechanics” – Springer, 2004. – С. 1–30.