Достоверность и точность геоданных

На сегодняшний день геопространственная разведка имеет значительную роль в современном мире. При помощи информационных технологий, имеется возможность оптимизировать алгоритмы, используемые в георазведке для построения данных. При помощи программ и алгоритмов, создаются модели на основе геоданных с учетом погрешностей, а также производится их анализ.

Для разработки объектов и их построения в пространстве требуются точки в пространственной системе координат. В целом основным условием истинности будет погрешность расположения объекта или точек в трехмерной области. Изначально следует обратить внимание на изучение влияние погрешностей и как следствие исследование итоговых замеров. Точки координат в пространстве, обычно, являются изменяемыми параметрами, так как описываются на основании общих измеряемых значениях, в частности линейниых и угловых. К примеру, лидарная сканировка, мензульная и электро-тахеометрия. Исходя из этого исследование безошибочного нахождения положения таких точек, разумно реализовывать при помощи точной котировки в аналогии вычисления итогов измерения с помощью математической обработки. Цель исследования является анализ и оценка точности геопространственных данных. Анализ геоданных выполняется в различных координатных системах, поэтому появляется потребность в независимом анализе безошибочности критериев, иными словами данные объективности от изменения параметров. Тензор погрешностей относится именно к таким критериям [1]. В частности для изотропности подбора координат подходящим инструментом для исследования геоданных будет тензор погрешностей.

Известно, для того чтобы точно оценить точность расположения точек в пространстве наиболее подходящей будет ковариационная матрица. В целом матрица выражается формулой и будет иметь вид:

                                                               (1)

где:  – среднеквадратичная ошибка погрешность;

Q – матрица.

Наиболее точную информацию об элементах которые нужно определить, можно найти именно с помощью этой матрицы. Более того она имеет все свойства, которые есть в тензоре, вернее матрица не изменяется по координатным осям. [1; 2]

Так как ковариационная матрица имеет признак неизменяемости, в данном случае ее следует линейно преобразовать с помощью формулы:

                                                     (2)

где:  – измененная матрица;

 – переменный оператор;

 – транспонированный символ.

В случае если точка пространства вычисляется при учете измеряемых линий и углов, то ее координаты, тогда положение точки, обычно, будет являться зависимой величиной, тогда матрица будет содержать моменты корреляции, которые не будут равны нулю. Матрица в координатной системе (X, Y, Z) для единичного пункта, будет представлять следующее значение:

K=                                                (3)

где:  – среднеквадратичные ошибки пункта по осям координат;

 – моменты корреляции.

Так как ковариационная матрица качеством неизменности, тогда она будет симметрична по отношению к основной диагонали, где находятся квадраты среднеквадратичных погрешностей. Из чего можно заключить .

Аналогичный элемент диагонали ковариационной матрицы K очевидно высчитывается из следующей формулы:

                              (4)

здесь  – производная частного вектора линейных функции в результате итоговых измерений;

 – результат измерений обратных весов матрицы;

 – коэффициент уравнения матрицы;

 – коэффициент матрицы, получаемые уравниванием.

Общая формула вида пунктов не диагональной ковариационной матрицы, будет иметь следующий вид:

                                    (5)

Оценить и определить положение точки в области можно с помощью сферической координатной системе. Чтобы перейти от прямоугольной координатной системы в сферическую, будем иметь следующее выражение:

=                                                                  (6)

Так как матрица имеет те же свойства что и тензор, соответственно имеет те же ошибки и погрешности, то нетрудно перейти к точности оценок в сферической координатной системе. Исходя их этого данный оператор будет иметь вид:

U= 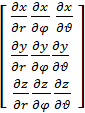                                                                               (7)

ли с учетом (6) можно записать:

Y= 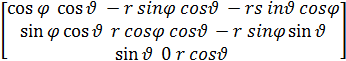                       (8)

Из выражения (2) следует вычислить априорную матрицу для того, чтобы оценить нахождения точки в пространстве в сферической координатной системе:

                                                                (9)

Либо

                                                       (10)

где:  – среднеквадратичная погрешность протяженности вектора ;

 – среднеквадратичная погрешность угла ;

 – среднеквадратичная погрешность угла .

Для того, чтобы детализировано произвести анализ точного пространственного расположения данных, нужно принять корреляцию связей. Для этой цели необходимо данное выражение применить для того, чтобы вычислить коэффициент зависимости одного значения от другого:

                                                            (11)

Здесь  – пункты матрицы (диагональные) K ;

 – фактор корреляции недиагонального элемента.

При этом полезно составить нормированную матрицу, состоящую из коэффициентов корреляции .

Так для анализа зависимостей пространственного положения пункта, выраженного матрицей K (3), запишем в виде матрицы

                                                  (12)

где:  – нормированная матрица;

                                                         (13)

В данном случае нормированная матрица  может быть использована чтобы анализировать действие погрешностей пунктов расположении в самомпространстве. В общем случае матрица  нужна чтобы, выявить анизотропию обоюдного действия функций стохастических значений.

Важным критерием оценки точности пространственного положения объектовявляется эллипсоид погрешностей. Такой критерий целесообразно использовать для выявления и анализа геометрических характеристик трехмерных изображений При разрешений и расчетов геопространственных, геофизических и других задач свойства каждой модели могут иметь различные значения для разных направлений в пространстве. Такие различия в значениях характеристик вариограмм для разных направлений выражают анизотропию в поведении параметра. Геометрическая интерпретация анизотропии в трехмерном пространстве может быть представлена при помощи поверхности эллипсоида, выражающей изменчивость параметров по различным направлениям. Главные оси анизотропии будут соответствовать трем взаимно перпендикулярным осям пространственного эллипсоида.

Свойства ошибок эллипосоида а так же его параметры определяются по формулам Коробкова С.А или Кардано [4].

В теории вероятности трехосный эллипсоид погрешностей рассматривается как область случайного попадания точки (с координатами x, y, z), подчиняющейся нормальному закону распределения [5].

Уравнение эллипсоида равной плотности Bk в канонической форме примет вид

                                     (14)

где: k – отношение полуосей эллипсоида погрешностей к главным стандартным отклонениям; - среднеквадратичное отклонения по координатной оси [5].

Вероятность попадания точки в трехосный эллипсоид погрешностей будет [3]

(15)

Либо

               (16)

Здесь  – является распределение функции нормали. В целом данная функция имеет вид:

                                         (17)

Далее совершим расчеты по формуле (16) при разных значениях .

Итоги этих расчетов, которые показывают вероятность появления точки внутри эллипсоида погрешностей, показаны в таблице 1.

Таблица 1.

Итог расчета погрешностей