РАСЧЕТ МАКСИМАЛЬНОЙ ТОЛЩИНЫ СРЕЗА ПРИ ПЛОСКОМ ГЛУБИННОМ ШЛИФОВАНИИ ПЕРИФЕРИЕЙ КРУГА
Секция: Технические науки

LIX Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
РАСЧЕТ МАКСИМАЛЬНОЙ ТОЛЩИНЫ СРЕЗА ПРИ ПЛОСКОМ ГЛУБИННОМ ШЛИФОВАНИИ ПЕРИФЕРИЕЙ КРУГА
Введение
Процессы глубинного и высокоскоростного шлифования коренным образом изменили подходы к обработке хвостовиков лопаток турбин. Никелевые сплавы очень чувствительны к нагреву, прижогам и деформациям, имеющим место при традиционном шлифовании, поэтому обработка элементов хвостовика производилась очень медленно и тщательно, что требовало больших затрат времени. Используемая в настоящее время технология глубинного шлифования позволяет выполнять черновую и отделочную обработку с высокой производительностью и качеством.
Ранее Маслов Е.Н. в своей книге «Теория шлифования материалов» [1] использовал параметрические уравнения циклоиды (1), (2).
![]() , (1)
, (1)
![]() , (2)
, (2)
Данные уравнения позволили автору вывести формулы для определения максимальной толщины среза amax, при плоском маятниковом шлифовании периферией круга. Преимуществом выведенных формул в том, что их можно использовать на практике без применения специализированного программного обеспечения. Недостатком данных формул является, то, что при использовании уравнений (1) и (2) невозможно оценить общий вид процесса. Для описания любого процесса гораздо эффективнее использовать дифференциальную форму. Данный метод является более трудоемким, но при использовании ПК процесс расчета можно автоматизировать. Так как процессы глубинного и плоского маятникового шлифования имеют отличительные особенности с точки зрения режимов резания и кинематики, произведем расчет amax для глубинного шлифования периферией шлифовального круга в пределах одного оборота шпинделя станка. Чтобы определить закономерности, выведем формулу для определения максимальной толщины среза в пределах одного оборота шпинделя amax при встречном шлифовании. Схема расчета максимальной толщины среза (рисунок 1).
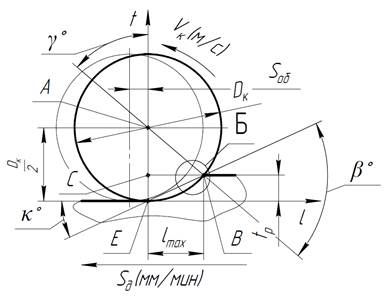
Рисунок 1. Схема для расчета максимальной толщины среза
Исходные данные: Vк (м/с), Dк (мм), tр (мм), Sд (мм/мин). Выходной параметр amax – максимальная толщина среза (мм).
Рассмотрим зависимость между параметрами t, Dк и l при Sд = 0.
Исходя из рисунка 1 параметр tр рассчитывается по выражению (3)
![]() , (3)
, (3)
После решения уравнения получим формулу (4).
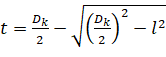 , (4)
, (4)
Выразим из формулы (4) параметр l, получим формулу (5).
 , (5)
, (5)
После упрощения формулы (5) получим дифференцированное уравнение циклоиды в общем виде (6) [4].
![]() , (6)
, (6)
Исходя из рисунка 1 шлифовальный круг переместится на величину Sоб по оси l, где Sоб (мм/об) подача на один оборот шпинделя. В результате получены периодические конечные графики функции с периодом Sоб (мм/об) ограниченные Dк/2 (рисунок 2).
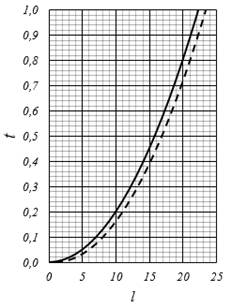
Рисунок 2. Периодические конечные графики функции t(Dк/2, l), с периодом Sоб (мм/об) ограниченные Dк/2; l(мм); t(мм)
Основной линией изображен конечный график t(Dк/2, l) исходного состояния заготовки в процессе резания. Пунктирной линией изображен конечный график после выполнения условия Sоб = 1 мм/об, при Dк=500 мм.
Для того чтобы определить величину аmax рассмотрим вид Б (рисунок 3).

Рисунок 3. Расчетная схема для определения аmax
Величина аmax это высота треугольника BKM, a Δ – это погрешность расчета аmax. Относительная погрешность расчета, составляет 0,02…0,2%, в зависимости от параметров Dк, t. В результате получим выражение (7).
![]() , (7)
, (7)
После вычисления стороны MN получим выражение (8).
![]() , (8)
, (8)
Угол α рассчитывается по формуле (9)
![]() , (9)
, (9)
где dl определяется условием (10), а dt – это расстояние по оси t между функциями t(Dк/2, l) до и после совершения одного оборота шпинделя.
![]() , (10)
, (10)
где Sоб рассчитывается по формуле (11)
![]() , (11)
, (11)
где, Sд минутная подача, а n частота вращения шпинделя станка.
Формула (12) предназначена для определения длинны дуги шлифовального круга участвующего в контакте с деталью. Схема (рисунок 1)
![]() , (12)
, (12)
где ɣ° – формула (13)
![]() , (13)
, (13)
где β° – формула (14)
![]() , (14)
, (14)
Параметр l рассчитывается по формуле (5).
Угол α° рассчитывается по формуле (15)
![]() , (15)
, (15)
Переведем ɣ° в ɣрад при помощи формулы (16)
![]() , (16)
, (16)
Формула (12) численно соответствует формуле (17), выведенная Масловым Е.Н. [1], [2], [3].
![]() , (17)
, (17)
Площадь контакта шлифовального круга с заготовкой рассчитывается по формуле (18) [1]
![]() , (18)
, (18)
где B – высота шлифовального круга участвующего в контакте с обрабатываемой заготовкой.
Пример расчета amax изображен на рисунке 4.
Выводы:
В результате расчета amax было выведено дифференцированное уравнение циклоиды (6) [4].
![]() , (6)
, (6)
Данным уравнением можно описать практически любой процесс механической обработки. Различие состоят только в том, что процесс происходит в разных проекциях и координатных четвертях.
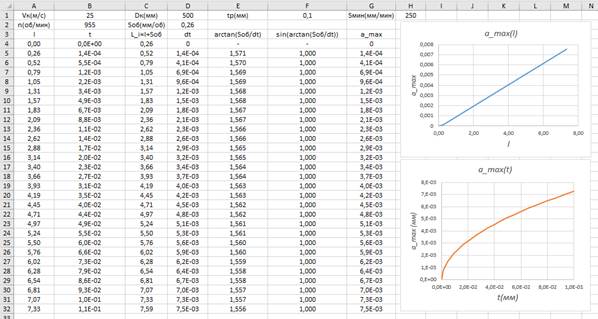
Рисунок 4. Пример расчета amax при Vк=25(м/с), Dк=500(мм), Sд=250(мм/мин), tр=0,1 мм
Так при расчете было выяснено, параметр tр и Dк в большей мере влияют на Lк. Зависимости Lк(tр, Dк) изображены на рисунке 5

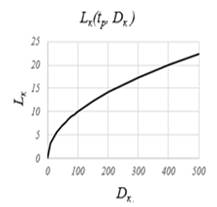
Рисунок 5. Слева (график Lк(tр, Dк ) при Dк =500 мм; Lк(мм); tр(мм));справа график Lк(tр, Dк ) при tр =1 мм; Lк(мм); Dк (мм)
По такой же закономерности, что и графики (рисунок 5), изменяется amax, относительно tр (рисунок 4). Изменение amax относительно l изменяется по линейному закону (рисунок 4). График зависимости amax от Sмин изображен слева на (рисунок 6). График зависимости amax от Vк изображен справа на (рисунок 6)
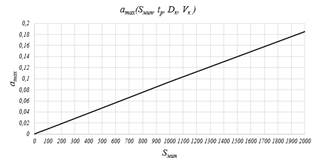
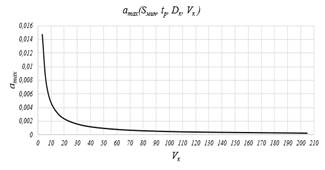
Рисунок 6. Слева график amax(Sмин, tр, Dк, Vк ), при tр=1(мм), Dк=500(мм), Vк=25(м/с); Sмин(мм/мин), amax(мм); справа график amax(Sмин, tр, Dк, Vк ), при tр=1(мм), Dк=500(мм), Sмин=25(мм/мин); Vк(м/с), amax(мм)
Исходя из можно сделать вывод, что при увеличении Vк уменьшается amax, что позволяет увеличить Sд и tр, а значит повысить производительность обработки.
За счет широкого диапазона режимов резания, разнообразия СОТС и режущего инструмента, можно обеспечить бездефектную обработку. [2], [3].
Но большое многообразие процесса, не позволяет описать все закономерности, поэтому каждый отдельный случай необходимо рассматривать отдельно.
Из рисунка 7 видно, что повышение Vк от 150 м/с и выше не приводит к уменьшению параметра amax., а значит рост производительности останавливается.
При глубине резания tр ≈ 2 мм, рост производительности останавливается на отметке в Vк=250 м/с. Скорость шлифовального круга Vк=250 м/с соответствует верхней границе производительного глубинного шлифования.
Выведенные формулы справедливы и для расчета толщины среза одним зубом фрезы при цилиндрическом фрезеровании, для этого необходимо к выше выведенным формулам добавить выражение (19).
![]() , (19)
, (19)
где nz – количество зубьев фрезы (шт.)
Рисунок 7 объясняет с точки зрения толщины среза переход из традиционного фрезерования в высокоскоростное фрезерование, с последующим переходом на глубинное шлифование в высокопроизводительное глубинное шлифование.





