Исследование системы видения методом Фурье анализа
Секция: Физико-математические науки

XXI Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Исследование системы видения методом Фурье анализа
На сегодняшний день обработка и анализ данных становятся всё более значимыми во многих областях. При решении климатических задач встаёт необходимость определения тенденций изменения различных характеристик. Главным средством анализа реальных физических процессов служит гармонический анализ, в частности, анализ Фурье [2],[3].
Будем рассматривать сигнал как модель описания физического процесса, способную передавать информацию и описанную математически с помощью функций определенного типа или полученную в результате натурных, лабораторных или численных экспериментов.
В теории излучения активно используют понятия система и линейная система. Под системой видения понимается система наблюдения, включающая в себя подстилающую поверхность, рассеивающую и поглощающую среду, и оптическое устройство, осуществляющее регистрацию приходящего излучения.
Для анализа данной системы был использован приём исследования системных характеристик, а именно функции размытия точки. Эта характеристика представляет собой отклик линейной системы на ![]() -импульс, по которому можно судить о свойствах рассматриваемой системы, то есть фактически о свойствах атмосферы. Если нет искажений, то есть атмосфера абсолютно чистая, а приёмник идеальный, то в этом случае изображением точечного источника на любой рассматриваемой высоте будет представлять собой точечный источник (точку). В случае, когда атмосфера замутнена
-импульс, по которому можно судить о свойствах рассматриваемой системы, то есть фактически о свойствах атмосферы. Если нет искажений, то есть атмосфера абсолютно чистая, а приёмник идеальный, то в этом случае изображением точечного источника на любой рассматриваемой высоте будет представлять собой точечный источник (точку). В случае, когда атмосфера замутнена ![]() -импульс размывается, таким образом вместо точки будет видно пятно. В связи с этим, чем мутнее атмосфера, тем шире становится размытие. Физически функция размытия точки является решением уравнения переноса, не имеющего точного решения [1].
-импульс размывается, таким образом вместо точки будет видно пятно. В связи с этим, чем мутнее атмосфера, тем шире становится размытие. Физически функция размытия точки является решением уравнения переноса, не имеющего точного решения [1].
Исследование системы видения было проведено на основании анализа функции размытия точки, поскольку с её использованием можно получить изображение произвольного объекта, что и являлось конечной целью.
Исходные данные
Численные данные, используемые в данном эксперименте с целью проведения над ними гармонического анализа, представляли собой результаты расчетов функций размытия точки систем видения через атмосферу методом Монте-Карло для различных условий наблюдения. Длина волны – 0,55 мкм, безоблачная атмосфера, модель Жаклин Ленобль. Наблюдение вертикально вниз.
Приведем краткое описание условий наблюдения:
1) Ламбертовский точечный источник, приземный слой соответствует модели Ленобль, в следующем слое коэффициент ослабления 0.1 обратных километров.
2) Ламбертовский точечный источник, приземный слой соответствует модели Ленобль, в следующем слое коэффициент ослабления 0.15 обратных километров.
В приведённых ниже рисунках 1-5 условия наблюдения для функции размытия точек 1) - 2) соответствуют графикам А) - Б).
Результаты моделирования
Была проведена серия экспериментов, выполнены обработка и анализ результатов статистических экспериментов, направленных на установление закономерностей трансформации излучения в системах видения.
В качестве исходных данных программе подавались функции размытия точки ![]() (яркость), графики которой представлены на рисунке 1.
(яркость), графики которой представлены на рисунке 1.
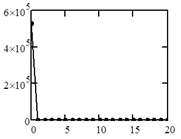

А) Б)
Рисунок 1 функция размытия (яркость) ![]() , соответствующая условиям наблюдения 1) - 2)
, соответствующая условиям наблюдения 1) - 2)
В соответствии с прозрачностью атмосферы функция размытия точки не значительно отличается от ![]() -функции, однако отличие всё же есть. Спектрограмма (Фурье образ) рассматриваемой функции
-функции, однако отличие всё же есть. Спектрограмма (Фурье образ) рассматриваемой функции ![]() представляет собой полосу, также как и для
представляет собой полосу, также как и для ![]() -функции (Рисунок 2). То есть атмосфера не замутнена, поэтому все частоты передаются приблизительно одинаково.
-функции (Рисунок 2). То есть атмосфера не замутнена, поэтому все частоты передаются приблизительно одинаково.

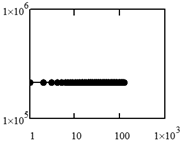
А) Б)
Рисунок 2. Спектрограмма функции ![]() , соответствующая условиям наблюдения 1) - 2)
, соответствующая условиям наблюдения 1) - 2)
Произвольный объект на поверхности земли был представлен в виде комбинации синусов (Рисунок 2) и имел следующий вид:
![]() .
.
Стояла задача выяснить, как данный объект будет виден через атмосферу. Для этого над функцией размытия точки ![]() и над объектом
и над объектом ![]() был проведён алгоритм прямого преобразования Фурье
был проведён алгоритм прямого преобразования Фурье ![]() (Рисунок 2) и
(Рисунок 2) и ![]() (Рисунок 3) соответственно.
(Рисунок 3) соответственно.
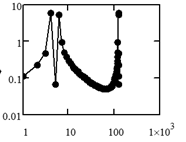
Рисунок 3. Спектрограмма функции ![]()
Далее была выполнена свёртка полученных результатов в частотной области, результат которой представлен на рисунке 4.
![]() .
.

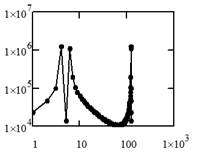
А) Б)
Рисунок 4. Свёртка ![]() , соответствующая условиям наблюдения 1) - 2)
, соответствующая условиям наблюдения 1) - 2)
С использованием обратного преобразования Фурье было восстановлено изображение объекта на верхней границе атмосферы (Рисунок 5).
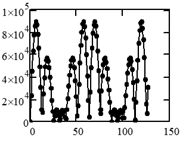

А) Б)
Рисунок 5. Изображение объекта ![]() на верхней границе атмосферы, соответствующее условиям наблюдения 1) - 2)
на верхней границе атмосферы, соответствующее условиям наблюдения 1) - 2)
В заключение хочется отметить, что существует немало методов и моделей, используемых при обработке сигналов. В данной работе показано применение преобразования Фурье для обработки данных, полученных в результате имитационного моделирования (а именно метода Монте-Карло, считающегося универсальным способом решения задач оптики атмосферы), с целью проведения исследования характеристик систем видения через атмосферу. В результате выполненного анализа Фурье были получены изображения объектов, расположенных на верхней границе атмосферы при различных условиях наблюдений.





