Повышение энергетической эффективности систем радиосвязи с использованием перестановочных алгоритмов декодирования блоковых избыточных кодов
Конференция: LVII Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Технические науки

LVII Студенческая международная научно-практическая конференция «Молодежный научный форум»
Повышение энергетической эффективности систем радиосвязи с использованием перестановочных алгоритмов декодирования блоковых избыточных кодов
Передаваемая по каналам связи дискретная информация в случае искажения данных не может получить верную оценку степени данных искажений, так как она не обладает избыточностью. В цифровую информацию вводят избыточность искусственно для исключения влияния помех на цифровые системы связи.
Применение стирающего канала связи является наиболее простым способом повышения спектральной эффективности системы. Но данный метод имеет ряд недостатков, наиболее существенным из которых является большое число ложных стираний и, как следствие, потеря информации. Таким образом возникла целесообразность использования более тонкого механизма в виде помехоустойчивых кодов для повышения энергетической эффективности систем связи. Самым лучшим методом является метод перестановочного декодирования, позволяющий исправить большее число ошибок за пределами метрики Хэмминга, чем применение стирающего канала связи.
Рассматриваемый метод относится к системам мягкой обработки данных и заключается в использовании более надежных символов на приеме.
Групповой код представляется в виде: (n, k, d) или (n, k, dmin) и описывается такими параметрами как n – длина кодового вектора, k – число информационных символов, dmin – минимальный вес кодовой комбинации). Любой групповой код способен исправить t = (d – 1) / 2 ошибок, при этом тот же код способен обнаружить s = d – 1 ошибок.
Благодаря использованию метрики Хэмминга в формате введенной в код избыточности и определяемой как разность (n – k), вместо расстояния Хэмминга dmin, достигается получение дополнительного энергетического выигрыша.
Рассмотрим сам метод перестановочного декодирования на примере выполнения перестановочного декодирования при наличии ошибок.
Способы применения помехоустойчивого декодирования лежат в основе реализации методов повышения энергетической эффективности и важное место в данном процессе занимают методы обработки принятых данных на приемной стороне.
Для наглядности выполним перестановочное декодирование, взяв для примера групповой код (7,4,3). Нам так же известно, что максимальное количество ошибок, которое мы можем исправить равно n-k, т.е. 3. Проверим это на практике путем введения трех ошибок.
Для удобства воспользуемся программой MathCad.
Пусть на выходе приемника был получен кодовый вектор ![]() .
.
Первым шагом необходимо расположить элементы кода по степени надежности и составить матрицу перестановок. Для этого необходимо расположить элементы кода в порядке убывания оценки, т.е. по степени надежности, при этом добавим ошибку в принятый код.
Степень надежности элементов можно рассчитать по формуле, а можно принять заданной. В данном примере оценки зададим случайным образом (максимальная оценка - 7, минимальная - 0).
Расположим элементы кода по степени надежности и составим матрицу перестановок. Для этого необходимо расположить элементы кода в порядке убывания оценки, т.е. по степени надежности, при этом допустим в принятии кода 3 ошибки – в 3, 4 и 6 символе.
Таблица 1.
Оценка каждого элемента принятого кода
номер |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
Оценка |
7 |
7 |
3 |
1 |
7 |
2 |
7 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
Оценка |
7 |
7 |
3 |
1 |
7 |
2 |
7 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
Оценка |
7 |
7 |
7 |
7 |
3 |
2 |
1 |
Формируем матрицу перестановок.
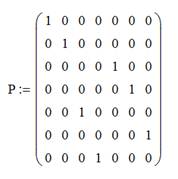
Таблица 2.
Расстановка элементов в порядке уменьшения степени надежности
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
Оценка |
7 |
7 |
3 |
2 |
7 |
1 |
7 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
Оценка |
7 |
7 |
7 |
7 |
3 |
2 |
1 |
2. Для нахождения эквивалентного кода необходимо получить порождающую матрицу эквивалентного кода в систематической форме. Для этого необходимо истинную порождающую матрицу исходного кода переставить в соответствии
с перестановкой принятого вектора. 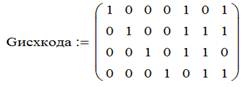 ,
,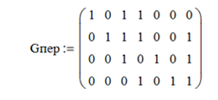 .
.
Составляем квадратную матрицу G11, соответствующую четырем наиболее надежным символам.

Находим определитель матрицы. ![]() , следовательно, может быть найдена обратная матрица.
, следовательно, может быть найдена обратная матрица.
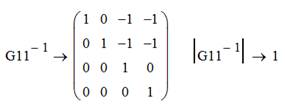
Определитель обратной матрицы так же не равен нулю, можем привести перестановочную матрицу к систематической форме.
Порождающая матрица в систематической форме:

Определим вектор с надежно принятыми символами: ![]()
Получим комбинацию эквивалентного кода:
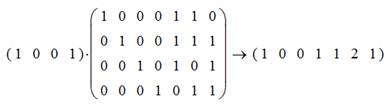
Т.к. ![]() , комбинация эквивалентного кода выглядит следующим образом: (1001101).
, комбинация эквивалентного кода выглядит следующим образом: (1001101).
Сложим по mod2 вектор переставленного кода с вектором эквивалентного кода и получим вектор ошибок:
Таблица 3.
Результат нахождения вектора ошибки
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
![]() .
.
Чтобы исправить ошибки, необходимо умножением полученного вектора ошибок на транспонированную матрицу перестановок определить местонахождение ошибки, а затем сложить результат по mod2 с принятым вектором.
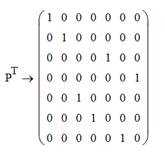 ,
, 
е=(0011010)
Отсюда можем сделать вывод о том, что ошибка находится в 3, 4 и 6 символе.
Таблица 4.
Нахождение ошибки
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
е |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
Таким образом, исправленный вектор ![]() = .
= .![]()
С целью исключения влияния помех на цифровые системы связи, в цифровую информацию искусственно вводится избыточность, благодаря чему удается выявить и исправить ошибки.
Наиболее эффективным методом получения энергетического выигрыша в системах связи является метод перестановочного декодирования. Для кода (7,4,3) может быть исправлено до 3-х ошибок, в то время как при применении стирающего канала связи может быть исправлена 1 и обнаружены 2 ошибки. А так же, при выработке приемником шести мягких решений символов кодовых комбинаций в системе мягкого декодирования помехоустойчивых кодов обеспечивается энергетический выигрыш до трех дБ, что дает огромный экономический выигрыш при использовании данного метода крупными компаниями (например, космическими системами связи).
Список литературы:
1.Гладких А. А. Обобщенный метод декодирования по списку на базе кластеризации пространства кодовых векторов // Радиотехника. – 2015. – №6.
2.Гладких А.А. Основы теории мягкого декодирования избыточных кодов в стирающем канале связи. – Ульяновск: УлГТУ, 2010.
3.Зяблов, В. В., Коробков Д. Л., Портной С. Л. Высокоскоростная передача сообщений в реальных каналах. – М. : Радио и связь, 1991.





