Анализ корреляционной зависимости цены нового автомобиля «Ауди» и его технических характеристик
Секция: Экономика

LIII Студенческая международная научно-практическая конференция «Молодежный научный форум: общественные и экономические науки»
Анализ корреляционной зависимости цены нового автомобиля «Ауди» и его технических характеристик
Сегодня сложно представить свою жизнь без автомобилей. С каждым годом появляется все больше различных моделей, а иногда и марок авто, а увеличение темпа жизни, ведет к постоянному росту их количества. В России все чаще можно наблюдать такую ситуацию, когда в одной семье в пользовании находится не один, а два и более автомобиля, что свидетельствует о постоянном увеличении спроса на них.
Транспортные средства являются не просто средствами для передвижения, но и зачастую предметами роскоши.
Одной из подобных премиальных марок авто является «Ауди». Данная компания предоставляет широкий выбор классов автомобиля и различных опций для него, которые могут значительно увеличивать его цену и выбор в пользу одних или других часто бывает затруднителен. Чтобы облегчить данный выбор, необходимо понимать, от каких технических характеристик в большей степени зависит цена авто и на что в первую очередь стоит обращать внимание при его выборе. Этим обусловлена актуальность данной работы.
Объектом данной работы является рыночная цена нового автомобиля «Ауди».
В качестве предмета данного исследования выступает анализ корреляционной зависимости цены нового авто и его различных технических характеристик.
Цель данного исследования предполагает разработку оптимальной модели множественной регрессии, отражающей взаимосвязь между ценой нового автомобиля и его техническими характеристиками.
Для достижения поставленной цели необходимо выполнение ряда задач, таких как построение и анализ регрессионной модели, а также экономическая интерпретация различных ее элементов.
Цена любого технически сложного изделия, которым является автомобиль определяется в первую очередь его техническими характеристиками. В данной работе рассматриваются такие технические параметры автомобиля, как объём двигателя (Л), мощность двигателя (л.с.), тип коробки передач и тип привода автомобиля. Однако нужно обязательно учитывать и класс автомобиля, поэтому регрессионная модель, по нашему мнению, должна строиться с учетом этого показателя.
Таким образом, в качестве исходных данных имеем массив, включающий значения двух количественных и трех качественных переменных, которые преобразуются в фиктивные переменные (см. Табл. 1).
Таблица. 1
Исходные данные для эконометрического анализа, 2017 г.
|
№ |
Название |
Y |
X1 F1 |
X1 F2 |
X2 |
X3 F |
X4 F1 |
X4 F2 |
X5 |
|
1 |
Audi a3 |
1639000 |
0 |
0 |
1,4 |
0 |
1 |
0 |
150 |
|
2 |
Audi a3 |
1710000 |
1 |
0 |
1,4 |
0 |
1 |
0 |
150 |
|
3 |
Audi a3 |
1975000 |
1 |
0 |
2,0 |
0 |
1 |
0 |
190 |
|
4 |
Audi a3 |
2059000 |
1 |
0 |
2,0 |
1 |
1 |
0 |
190 |
|
5 |
Audi a4 |
1840000 |
0 |
0 |
1,4 |
0 |
1 |
0 |
150 |
|
6 |
Audi a4 |
1920000 |
1 |
0 |
1,4 |
0 |
1 |
0 |
150 |
|
7 |
Audi a4 |
2020000 |
0 |
0 |
1,4 |
0 |
1 |
0 |
150 |
|
8 |
Audi a4 |
2020000 |
0 |
0 |
1,4 |
0 |
1 |
0 |
150 |
|
9 |
Audi a4 |
2100000 |
1 |
0 |
1,4 |
0 |
1 |
0 |
150 |
|
10 |
Audi a4 |
2100000 |
1 |
0 |
1,4 |
0 |
1 |
0 |
150 |
|
11 |
Audi A8 |
6643000 |
0 |
1 |
3,0 |
1 |
0 |
0 |
310 |
|
12 |
Audi A8 |
7643000 |
0 |
1 |
4,0 |
1 |
0 |
0 |
435 |
|
13 |
Audi A8 |
6390000 |
0 |
1 |
3,0 |
1 |
0 |
0 |
310 |
|
14 |
Audi A8 |
7390000 |
0 |
1 |
4,0 |
1 |
0 |
0 |
435 |
|
15 |
Audi a4 |
2170000 |
0 |
0 |
2,0 |
0 |
1 |
0 |
190 |
|
16 |
Audi a4 |
2170000 |
0 |
0 |
2,0 |
0 |
1 |
0 |
190 |
|
17 |
Audi a4 |
2250000 |
1 |
0 |
2,0 |
0 |
1 |
0 |
190 |
|
18 |
Audi a4 |
2250000 |
1 |
0 |
2,0 |
0 |
1 |
0 |
190 |
|
19 |
Audi a4 |
2584000 |
1 |
0 |
2,0 |
1 |
1 |
0 |
190 |
|
20 |
Audi a4 |
2584000 |
1 |
0 |
2,0 |
1 |
1 |
0 |
190 |
|
21 |
Audi a6 |
2980000 |
0 |
0 |
1,8 |
0 |
0 |
1 |
190 |
|
22 |
Audi a6 |
3051000 |
1 |
0 |
1,8 |
0 |
0 |
1 |
190 |
|
23 |
Audi a6 |
3283000 |
1 |
0 |
2,0 |
0 |
0 |
1 |
252 |
|
24 |
Audi a6 |
3385000 |
1 |
0 |
2,0 |
1 |
0 |
1 |
249 |
|
25 |
Audi a6 |
3300000 |
1 |
0 |
2,0 |
0 |
0 |
1 |
252 |
|
26 |
Audi a6 |
4049000 |
1 |
0 |
3,0 |
1 |
0 |
1 |
333 |
|
27 |
Audi a6 |
3514000 |
1 |
0 |
2,0 |
1 |
0 |
1 |
249 |
|
28 |
Audi a6 |
4177000 |
1 |
0 |
3,0 |
1 |
0 |
1 |
333 |
|
29 |
Audi RS6 |
8525000 |
1 |
0 |
4,0 |
1 |
0 |
1 |
605 |
|
30 |
Audi a7 |
2355000 |
1 |
0 |
2,0 |
0 |
0 |
0 |
190 |
Исходный массив содержит данные о цене Y тридцати автомобилей ауди с указанием объема двигателя (X2), мощности (X5). В данной модели присутствует два многозначных качественных признака, поэтому были введены следующие фиктивные переменные:
1) X1 F1 – цифрой 1 обозначается роботизированная коробка передач, а цифрой 0 иная;
2) X1 F2 – цифрой 1 обозначается автоматическая коробка передач, цифрой 0 иная КПП;
3) X4 F1 - цифрой 1 обозначается компакт класс, цифрой 0 иной класс автомобиля;
4) X4 F2 – цифрой 1 обозначается бизнес класс, цифрой 0 иной класс.
Также была введена бинарная переменная X3 F. Цифрой 1 обозначается полный привод, а цифрой 0 – передний привод автомобиля.
Построение регрессионной модели целесообразно начать с определения парных коэффициентов корреляции, характеризующих взаимосвязь между тем или иным объясняющим фактором и объясняемой переменной. Воспользовавшись встроенными возможностями «Microsoft Office Excel», получили следующие значения парных коэффициентов корреляции (см. Табл.2).
Таблица.2
Парные коэффициенты корреляции
|
rX1 F1Y |
rX1 F2Y |
rX2Y |
rX3 FY |
rX4 F1y |
rX4 F2y |
rX5Y |
|
-0,22376 |
0,751962 |
0,935261 |
0,670277 |
-0,69545 |
0,236465 |
0,937434 |
Значения парного коэффициента корреляции могут быть интерпретированы следующим образом:
· если |r|<0,3,то связь между переменными практически отсутствует;
· если 0,3≤|r|≤0,7, то связь средняя;
· если 0,7≤|r|≤0,9, то связь сильная;
· если 0,9≤|r|≤0,99, то связь весьма сильная.
Как видно из приведенной таблицы, между каждым из факторных и результативным признаками существует корреляционная зависимость разной степени интенсивности.
Далее рассчитаем множественный коэффициент детерминации 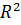 и множественный коэффициент корреляции
и множественный коэффициент корреляции 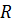 . Множественный коэффициент детерминации
. Множественный коэффициент детерминации 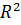 составляет 0,98 (или 98%), следовательно, множественный коэффициент корреляции
составляет 0,98 (или 98%), следовательно, множественный коэффициент корреляции 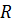 равен 0,99 (или 99%). Таким образом, вариация цены нового автомобиля «Ауди» на 98% зависит от вариации значений вышеуказанных технических параметров и на 2% - от вариации иных, неучтенных факторов (цвет автомобиля, вид колесных дисков и пр.).
равен 0,99 (или 99%). Таким образом, вариация цены нового автомобиля «Ауди» на 98% зависит от вариации значений вышеуказанных технических параметров и на 2% - от вариации иных, неучтенных факторов (цвет автомобиля, вид колесных дисков и пр.).
Для определения наличия в модели мультиколлинеарности воспользуемся матрицей парных коэффициентов корреляции (см. Табл. 3).
Таблица. 3
Матрица парных коэффициентов корреляции
|
|
Y |
X1 F1 |
X1 F2 |
X2 |
X3 F |
X4 F1 |
X4 F2 |
X5 |
|
Y |
1 |
|
|
|
|
|
|
|
|
X1 F1 |
-0,224 |
1 |
|
|
|
|
|
|
|
X1 F2 |
0,752 |
-0,515 |
1 |
|
|
|
|
|
|
X2 |
0,935 |
-0,146 |
0,675 |
1 |
|
|
|
|
|
X3 F |
0,670 |
0,056 |
0,480 |
0,706 |
1 |
|
|
|
|
X4 F1 |
-0,695 |
-0,018 |
-0,419 |
-0,632 |
-0,464 |
1 |
|
|
|
X4 F2 |
0,236 |
0,347 |
-0,257 |
0,202 |
0,208 |
-0,700 |
1 |
|
|
X5 |
0,937 |
-0,049 |
0,515 |
0,946 |
0,655 |
-0,665 |
0,373 |
1 |
Как показывает таблица, наибольшее влияние на цену, оказывает фактор X5 – мощность автомобиля (л.с.), затем следует фактор X2 – объём двигателя (л.), затем вид коробки передач X1 F2, после него X4 F1 – автомобиль компакт класса или же нет, затем X3 F – вид привода, затем X4 F2 – автомобиль бизнес класса или иной и X1 F1 – роботизированная КПП или иная.
Как мы видим, среди коэффициентов 5 и 6 столбцов есть такие значения, модуль которых превышает 0,7, следовательно, можно сделать вывод о наличии в модели мультиколлинеарных факторов. Явление мультиколлинеарности имеет ряд негативных последствий, а именно:
1. увеличение дисперсий оценок параметров, в результате чего снижается точность оценок;
2. статистическая неустойчивость МНК-оценок.
Чтобы исключить из модели это явление, применим метод «снизу-вверх». При этом подходе сначала выбирается простая модель, которая затем усложняется. При добавлении в модель нового фактора, должно проверяться 2 условия:
1) После добавления нового фактора, в получившейся модели нормированный 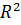 должен быть больше, чем в предыдущей;
должен быть больше, чем в предыдущей;
2) P – Значение при добавленном факторе должно быть меньше 0,05.
Если же оба этих условия выполняются одновременно, фактор оставляется в финальной модели.
Применив данный метод получили уравнение регрессии такого вида:
· Общее уравнение: 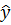 =692087,8-807359X2+17851,52X5+2500488X1 F2-267394X4 F1
=692087,8-807359X2+17851,52X5+2500488X1 F2-267394X4 F1
· Уравнение для авто с автоматической коробкой передач, но не компакт класса: 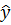 =3192575,4-807359X2+17851,5X5
=3192575,4-807359X2+17851,5X5
· Уравнение для авто не с автоматической коробкой передач, но компакт класса: 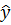 =424694-807359X2+17851,5X5
=424694-807359X2+17851,5X5
· Уравнение для авто не с автоматической коробкой передач и не компакт класса: 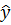 =692087,8-807359X2+17851,52X5
=692087,8-807359X2+17851,52X5
· Уравнение для авто с автоматической коробкой передач и компакт класса: 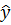 =3459969,2-807359X2+17851,52X5
=3459969,2-807359X2+17851,52X5
Для проверки значимости построенной модели воспользуемся F-тестом и проверим гипотезы о значимости коэффициента детерминации. Наблюдаемое значение F для построенной модели составляет 473.03, а критическое – 3,55. Так как 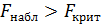 , гипотеза
, гипотеза 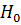 отвергается, справедлива конкурирующая гипотеза
отвергается, справедлива конкурирующая гипотеза 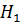 , следовательно, модель значима с достоверностью 98%.
, следовательно, модель значима с достоверностью 98%.
Построенная модель множественной регрессии может быть использована для прогнозирования рыночной цены новых автомобилей «Ауди», обладающих определенными техническими характеристиками.
Так, автомобиль с объёмом двигателя 1,6л, мощностью 180 л.с. не с автоматической коробкой передач и не компакт класса будет стоить 2613582,1р. или с достоверностью 98% от 1965264,6р. До 3261899,58р.
Таким образом, используя эконометрические методы, мы получили достаточно точную модель множественной регрессии, характеризующую зависимость между ценой нового автомобиля «Ауди» и его техническими характеристиками.
На основании проведенного исследования можно сделать вывод о том, что эконометрические методы являются важным инструментом исследования экономических процессов и явлений, происходящих на рынке, которые позволяют не только анализировать текущую ситуацию, но и прогнозировать возможные тенденции развития.





