МЕЖОТРАСЛЕВОЙ БАЛАНС В ЭКОНОМИЧЕСКИХ ЗАДАЧАХ

Исследования природы экономического роста повлекли за собой создание универсальных моделей, охватывающих все стороны развития. В их основу можно положить систему натуральных и стоимостных потоков, выступающих как результаты и издержки производства товаров и услуг. Данная задача сложна в экономическом и математическом аспектах. Первым решение предложил Фр. Кенэ в 1758 году. Он представил национальное хозяйство как систему баланса. Учёный полагал, что единственным производителем является сельское хозяйство, и весь поток продукции идёт из сельского хозяйства в остальную сферу экономики, которая приобретала эту продукцию.

Карл Маркс а также работники Госплана первых лет советской власти внесли свой неоценимый вклад в развитие модели народного хозяйства. Именно тогда были созданы заделы для более обширного применения межотраслевых моделей: динамических, оптимизационных, межрегиональных, натурально-стоимостных и других. В 1925 решающий шаг в создании подобных моделей осуществил выпускник петербургского университета Василий Леонтьев. Ему удалось представить в форме «шахматной таблицы» основные материальные и стоимостные потоки национального хозяйства. Преимущество модели было в том, что число данных потоков не ограничено, и оно зависит от объёма информации и вычислительных средств. Межотраслевой баланс производства и распределения общественного продукта с разбивкой на несколько сот отраслей составляется во многих странах мира, он позволяет оценить пройденный экономикой путь и прогнозировать ее развитие. За эту разработку межотраслевого баланса автор был награждён Нобелевской премией по экономике 1973 г.

В 70-х и 80-х годах в СССР на основе данных межотраслевых балансов разрабатывались более сложные межотраслевые модели, которые использовались в прогнозных расчетах и входили в технологию народнохозяйственного планирования. По ряду направлений советские межотраслевые исследования занимали достойное место в мировой науке. Тем не менее они не находили практического применения в производстве.

Рассмотрим матричную модель. Её центральным элементом является межотраслевой баланс. Он представляет собой экономико-математическую модель, характеризующую межотраслевые производственные взаимосвязи в экономике государства.

Существует несколько видов межотраслевых балансов. В основном существует градация по экономическому содержанию и характеру информации. По единицам измерения выделяются: стоимостные, натурально-стоимостные, натуральные. По объекту анализа балансы делятся на национальные и региональные. Эта характеристика особенно важна для Российской Федерации, так как важно создавать модели экономики не только для страны в целом, но и для её отдельных субъектов. Каждый из межотраслевых балансов, сгруппированных по единицам измерения и объекту анализа, может быть отчётным или плановым. По временному признаку балансы делятся на статистические и динамические. Статистические, часто совпадают с отчётными. Динамические используют оптимизационные модели, где приоритет отдаётся одному или нескольким важнейшим показателям.

При рассмотрении межотраслевого баланса часто сталкиваемся с такими понятиями, как «хозяйственные» и «чистые» отрасли. Различные организации производят товары и услуги не только по основному профилю своей деятельности. Например, сельскохозяйственное предприятие по мимо своего основного направления, может охватывать промышленную сферу и производить кирпич, гвозди т. д. В таком случае невозможно разрабатывать межотраслевой баланс. Поэтому используются чистые отрасли, принцип которых заключается в том, что из разноплановой деятельности по производству товаров и услуг выбирается только лишь одна профилирующая.

Рассмотрим общую структуру межотраслевого баланса. Он состоит из таблицы, характеризующей связи между отраслями в экономике. Предположим, что всего существует в данной системе n взаимосвязанных отраслей P1, Р2, ..., Рn. Валовой продукт i-й отрасли обозначим через Xi, где X1 — валовой продукт, P1, Х2 — валовой продукт Р2, ..., Хn   ― валовой продукт Рn). Конечный продукт каждой отрасли обозначим Y с индексом, соответствующим номеру элемента. Данные отрасли взаимосвязаны.

Пусть Xij — затраты продукции i-й отрасли на производство продукции Рj. Условно чистую продукцию i-й отрасли обозначим Vi. В данном случае речь идёт о стоимостном балансе. Под величинами Xi, Уj, Vj и Xij понимают выраженную в некоторых фиксированных ценах стоимость определённой продукции.

Всю информацию об экономической системе сведем балансовую таблицу.

Таблица состоит из четырёх квадрантов. Верхний левый квадрант характеризует межотраслевые потоки продукции. Сроки этого раздела показывают распределение продукции каждой отрасли на нужды других отраслей. Столбцы отражают структуру производственного потребления отраслей.

Правый верхний квадрант содержит два столбца, первый из которых содержит объёмы конечного продукта (продукция отрасли, предназначенная к потреблению в непроизводственной сфере), а второй ― величины общего объёма продукции.

Нижний левый квадрант содержит строку валовой продукции и строку величин условно-чистой продукции отраслей, включающих амортизационные отчисления, заработную плату и прибыль.

Данная таблица обладает несколькими важными свойствами. Для любой строки с номером от 1 до n справедливо соотношение баланса между производством и потреблением, означающее, что валовый продукт расходуется полностью, как на промежуточное, так и на конечное потребление.

Xi=∑Xij+Yi

Аналогично для любого столбца:

Xj=∑Xij+Vi

Величина Xij может быть представлена следующим образом:

Xij=aijXj

Величина Аij ― коэффициент прямых материальных затрат. Он показывает, какое количество продукции i-й отрасли требуется для производства единицы продукции j-й отрасли. Коэффициенты Аij считаются постоянными в межотраслевой модели.

Далее можно отметить:

Xi=∑aijXj+Yi

Представим это в следующем виде (матричный вид):

X = AX + Y (баланс распределения продукции)

где: X = (X1, X2,..., Xn) ― вектор валовых выпусков;

Y = (y1, y2,..., yn) - вектор конечного продукта;

A = -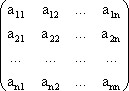

― матрица коэффициентов прямых материальных затрат.

X - AX = Y,

X (E - A) = Y,

Получим систему уравнений межотраслевого баланса, которая называется моделью Леонтьева.

Отсюда:

X = (E - A) ^-1Y,

где: E ― единичная матрица,

(E - A) ^-1=В — матрица полных материальных затрат.

Системы решаются с помощью балансовой модели, можно разделить на три группы:

1.  По заданному вектору конечного потребления Y найти вектор валового продукта.

2.  По заданному вектору валового выпуска вектора X, найти вектор конечного потребления Y.

3.  По изменению конечного продукта Y, найти межотраслевое перераспределение валового выпуска Х.

Далее рассмотрим следующий пример.

Таблица 1.

Для построения балансовых уравнений найдём коэффициенты прямых материальных затрат А_ij.

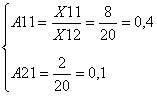
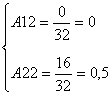
Составим систему балансовых уравнений:

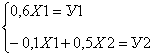
Решим первую задачу.

Определим вектор валового продукта X, если вектор Y=

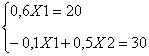
Решая данную задачу по формулам Крамера .

∆=0,3    ∆₁=10    ∆₂=19

X₁=33,3   X₂=63,3    X=

Определим вектор Y при заданном X=

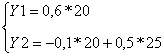
Y=

Найдём межотраслевое перераспределение валового выпуска продукции, если изменения конечного продукта.

∆Y=     

Матрица прямых материальных затрат (матрица А):

А₁₁=0,4  А₁₂=0,1  А₂₁=0  А₂₂=0,5

Межотраслевое перераспределение найдём из системы линейных уравнений.

∆Х = В*∆Y

∆Х=*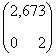

∆Х₁=43,35

∆Х₂=20

Межотраслевое перераспределение:

∆Х₁₁=0,4*43,35=17,34

∆Х₁₂=0,1*20=2

∆Х₂₁=0*43,35=0

∆Х₂₂=2*20=40

Решая подобные задачи можно прогнозировать валовый выпуск и межотраслевое перераспределение при изменении конечного продукта. Можно сделать вывод, что межотраслевой баланс позволяет всесторонне и комплексно охарактеризовать экономику, получить ёмкие показатели, открыть новые возможности для исследования общественного производства, изучить внутриотраслевые и межотраслевые связи, рассчитать коэффициенты прямых и полных материальных затрат. Также сочетание параметров межотраслевого баланса с дополнительной информацией даёт большое число производственных показателей, без которых трудно представить успех экономического анализа.

Список литературы:

1.           Коссов В.В. Межотраслевой баланс М: Экономика, 2009.

2.           Макаров С.И., Севастьянова С.А. Экономико-математические методы и модели. Задачник: учебно-практическе пособие. — М 6 КНОРУС, 2008. — 208 с.

3.           Межотраслевой баланс Леонтьева. — [Электронный ресурс] — Режим доступа. — URL: http://www.grandars.ru/student/nac-ekonomika/mezhotraslevoy-balans.html

4.          Модель межотраслевого баланса национальной экономики. — [Электронный ресурс] — Режим доступа. — URL: http://www.uchebnik-besplatno.com/ekonomicheskaya-teoriya-uchebnik/model-mejotraslevogo-balansa-natsionalnoy.html