Применение корреляционно-регрессионного анализа при изучении дефицита бюджета и государственного долга РФ
Секция: Экономика

VIII Студенческая международная научно-практическая конференция «Общественные и экономические науки. Студенческий научный форум»
Применение корреляционно-регрессионного анализа при изучении дефицита бюджета и государственного долга РФ
Аннотация. В проведенной работе ставится задача проведения корреляционно-регрессионного анализа государственного долга и бюджета РФ на основании некоторых статистических данных и оценки перспектив развития финансовой системы с 2018 по 2040 год с целью разработки возможных путей развития финансовой системы РФ и предположений по её укреплению.
Ключевые слова: корреляционно-регрессионный анализ, мультиколлинеарность, тест Фаррара-Глоубера, статистически значимая переменная, государственный долг, дефицит бюджета.
Одним из наиболее важных механизмов, позволяющих государству осуществлять экономическое и социальное регулирование, является финансовая система общества. Как известно, важнейшей задачей экономических исследований является выявление факторов, определяющих уровень и динамику экономического процесса. Такая задача может быть решена методами корреляционного и регрессионного анализа. Корреляционно-регрессионным анализом называется многообразие методов исследования параметров генеральной совокупности, распределенной по нормальному закону. В основе корреляционно-регрессионного анализа лежит взаимосвязь явлений природы и общества [3]. Цель нашего анализа – провести корреляционно-регрессионный анализ бюджета (доходы, расходы) и государственного долга РФ на основании некоторых факторных переменных, определить наиболее статистически значимые факторы для зависимой переменной Y и оценить их влияние на изучаемые явления. Рассмотрим корреляционно-регрессионный анализ доходов РФ, используя абсолютные значения доходов Российской Федерации за 2006-2017 год, где взяты следующие переменные[5]:
Y– всего доходов;
Х1 – нефтегазовые доходы;
Х2 – НДС;
Х3 – акцизы;
Х4 – налог на прибыль;
Х5 – налог на доходы физических лиц;
Х6 – ввозные пошлины;
Х7 – страховые взносы на обязательное социальное страхование;
Х8 – прочие.
Таблица 1.
Данные о доходах страны за 2006-2017 год
|
|
Y |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
|
2006 |
10 625,8 |
2 943,5 |
1 510,9 |
270,6 |
1 670,6 |
930,4 |
341,6 |
1 441,3 |
1 517,0 |
|
2007 |
13 368,3 |
2 897,4 |
2 261,5 |
314,4 |
2 172,0 |
1 266,6 |
488,0 |
1 980,8 |
1 987,6 |
|
2008 |
16 169,1 |
4 389,4 |
2 132,2 |
349,9 |
2 513,2 |
1 666,3 |
625,6 |
2 279,0 |
2 213,4 |
|
2009 |
13 599,7 |
2 984,0 |
2 050,0 |
347,2 |
1 264,6 |
1 665,8 |
467,2 |
2 300,5 |
2 520,3 |
|
2010 |
16 031,9 |
3 830,7 |
2 498,3 |
471,4 |
1 774,6 |
1 790,5 |
587,5 |
2 477,1 |
2 601,9 |
|
2011 |
20 855,4 |
5 641,8 |
3 250,4 |
650,5 |
2 270,5 |
1 995,8 |
692,9 |
3 528,3 |
2 825,1 |
|
2012 |
23 435,1 |
6 453,2 |
3 545,8 |
837,0 |
2 355,7 |
2 261,5 |
732,8 |
4 103,7 |
3 145,4 |
|
2013 |
24 442,7 |
6 534,0 |
3 539,0 |
1 015,8 |
2 071,9 |
2 499,1 |
683,8 |
4 694,2 |
3 404,9 |
|
2014 |
26 766,1 |
7 433,8 |
3 931,7 |
1 072,2 |
2 375,3 |
2 702,6 |
652,5 |
5 035,7 |
3 562,2 |
|
2015 |
26 922,0 |
5 862,7 |
4 234,0 |
1 068,4 |
2 599,0 |
2 807,8 |
565,2 |
5 636,3 |
4 148,8 |
|
2016 |
28 181,5 |
4 844,0 |
4 571,3 |
1 356,0 |
2 770,3 |
3 018,5 |
563,9 |
6 326,0 |
4 731,5 |
|
2017 |
30 640,0 |
5 971,9 |
5 137,6 |
1 521,3 |
3 290,1 |
3 252,3 |
588,5 |
6 523,9 |
4 354,4 |
Для начала необходимо найти матрицу парных коэффициентов корреляции с помощью функции КОРРЕЛ редактора Excel.
Таблица 2.
Матрица парных коэффициентов корреляции
|
|
у |
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
х8 |
|
Y |
1 |
|
|
|
|
|
|
|
|
|
x1 |
0,837447 |
1 |
|
|
|
|
|
|
|
|
x2 |
0,984042 |
0,749216 |
1 |
|
|
|
|
|
|
|
x3 |
0,973687 |
0,732824 |
0,980036 |
1 |
|
|
|
|
|
|
x4 |
0,787858 |
0,561736 |
0,808859 |
0,769688 |
1 |
|
|
|
|
|
x5 |
0,982415 |
0,764652 |
0,974006 |
0,969693 |
0,740057 |
1 |
|
|
|
|
x6 |
0,585259 |
0,794466 |
0,503239 |
0,42723 |
0,416472 |
0,531164 |
1 |
|
|
|
x7 |
0,983842 |
0,740029 |
0,986107 |
0,989149 |
0,766902 |
0,983686 |
0,451793 |
1 |
|
|
x8 |
0,949702 |
0,657461 |
0,959386 |
0,95624 |
0,703593 |
0,977614 |
0,426456 |
0,980764 |
1 |
Визуальный анализ матрицы парных коэффициентов корреляции позволяет установить: практически все независимые переменные анализа демонстрируют довольно высокие парные корреляции с другими независимыми переменными, что обуславливает необходимость проверки факторов на наличие между ними мультиколлинеарности. Для выявления мультиколлинеарности факторов выполним тест Фаррара-Глоубера по факторам Х1,Х4,Х6,Х7,Х8, который включает несколько этапов. Отметим, остальные же факторы были исключены, так как они имели наиболее высокую парную корреляцию с другими переменными, что усиливало явление мультиколлинеарности [1].
1. Проверка наличия мультиколлинеарности всего массива переменных с помощью матрицы межфакторных корреляций.
Таблица 3.
Матрица межфакторных корреляций в анализе дохода страны
|
|
х1 |
х4 |
х6 |
х7 |
х8 |
|
х1 |
1 |
0,561736 |
0,794466 |
0,740029 |
0,657461 |
|
х4 |
0,561736 |
1 |
0,416472 |
0,766902 |
0,703593 |
|
х6 |
0,794466 |
0,416472 |
1 |
0,451793 |
0,426456 |
|
х7 |
0,740029 |
0,766902 |
0,451793 |
1 |
0,980764 |
|
х8 |
0,657461 |
0,703593 |
0,426456 |
0,980764 |
1 |
Между факторами Х1 и Х6, Х1 и Х7, Х4 и Х7, Х4 и Х8, Х7 и Х8 наблюдается сильная зависимость (>0,7). Определитель det (R) = 0,000562 стремится к нулю, что позволяет сделать предположение об общей мультиколлинеарности факторов. 2. Проверка наличия мультиколлинеарности каждой переменной с другими переменными с помощью обратной матрицы.
Таблица 4.
Обратная матрица R-1
|
|
х1 |
х4 |
х6 |
х7 |
х8 |
|
х1 |
18,55374 |
6,389546 |
-10,5183 |
-49,9917 |
36,82161 |
|
х4 |
6,389546 |
5,082553 |
-3,80056 |
-22,8717 |
16,27559 |
|
х6 |
-10,5183 |
-3,80056 |
7,241995 |
27,57434 |
-20,5429 |
|
х7 |
-49,9917 |
-22,8717 |
27,57434 |
173,0242 |
-132,495 |
|
х8 |
36,82161 |
16,27559 |
-20,5429 |
-132,495 |
104,0469 |
Вычислив F-критерии по формуле 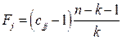 , где
, где  – диагональные элементы матрицы R-1, n=12, k = 5, получим, что значения F-критериев для всех факторов больше Fтабл= 4,39[2]. Это свидетельствует о наличии мультиколлинеарности между данными факторами.
– диагональные элементы матрицы R-1, n=12, k = 5, получим, что значения F-критериев для всех факторов больше Fтабл= 4,39[2]. Это свидетельствует о наличии мультиколлинеарности между данными факторами.
3. Проверка наличия мультиколлинеарности каждой пары переменных с помощью матрицы частных коэффициентов корреляции. Частные коэффициенты корреляции находим по формуле  и получаем:
и получаем:
Таблица 5.
Матрица частных коэффициентов корреляции
|
x1 |
1 |
-0,6579 |
0,907371 |
0,882302 |
-0,83805 |
|
|
|
x4 |
-0,6579 |
1 |
0,62658 |
0,77114 |
-0,70809 |
|
|
x6 |
0,907371 |
0,62658 |
1 |
-0,77878 |
0,74819 |
|
|
x7 |
0,882302 |
0,77114 |
-0,77878 |
1 |
0,98749 |
|
|
x8 |
-0,83805 |
-0,70809 |
0,74819 |
0,98749 |
1 |
Таблица 6.
Регрессионный анализ доходов страны за 2006-2017 год
|
ВЫВОД ИТОГОВ |
|
|
Регрессионная статистика |
|
|
Множественный R |
0,837078 |
|
R-квадрат |
0,700699 |
|
Нормированный R-квадрат |
0,634188 |
|
Стандартная ошибка |
4074,451 |
|
Наблюдения |
12 |
Из данной таблицы следует:
·уравнение множественной регрессии в линейной форме за счет значимых факторов имеет вид: ух=-8954,32+8,299959Х1+19,07574Х2;
·рассчитанный индекс корреляции (множественный R) R=0,837078, следовательно, связь сильная;
·коэффициент детерминации R2=0,700699 – около 70,06% вариаций результативного признака вызвано действием факторного признака;
·стандартная ошибка модели меньше стандартной ошибки (среднеквадратического отклонения) результативного признака (4074,451>7160,819). Наша модель точна.
Проанализируем статистическую значимость уравнения регрессии с помощью критерия Фишера. Поскольку Fрасч>Fтабл(10,53504>4,96), уравнение регрессии следует признать адекватным или статистически значимым. Оценив статистическую значимость параметров уравнения регрессии с помощью
Р-Значения, наблюдаем, что Р-значение переменной Х1(Х4)=0,009504, что означает, что она является высоко значимой для Y (меньше 0,01). Переменная Х2(Х6) не является значимой, так как её Р- значение = 0,155353 (больше 0,05). Таким образом, мы выявили статистически высоко значимый фактор – Х4.
Аналогичные анализы проводим и с расходами в РФ, внешним государственным долгом страны. В итоге получаем, что наиболее статистически значимым фактором, влияющим на формирование расходов в консолидированном бюджете страны, является национальная оборона. Факторные переменные внешнего государственного долга РФ хоть и влияют на размер государственного долга, но связь достаточно низкая, следовательно, объем государственного долга не достаточно сильно зависит от факторов, влияющих на них.
На основе статистических данных найдем точечный прогноз изменения величин общего объема доходов, расходов и государственного долга страны на период с 2018 по 2040 год с помощью линии тренда в Excel.

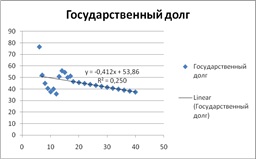
Рисунок 1. Тенденции развития консолидированного бюджета и внешнего государственного долга страны
Итак, на период с 2018-2040 гг. наблюдаются тенденции уменьшения величины внешнего государственного долга РФ и увеличения государственных расходов над доходами (дефицит бюджета), формирующихся под влиянием наиболее статистически значимых факторов, выявленных нами. Данная ситуация, с одной стороны, свидетельствует о дальнейших финансовых трудностях внутри страны, с другой же – о возможности возврата финансовой самостоятельности РФ за счет постепенного уменьшения госдолга. Таким образом, цель нашей работы достигнута, и данные, полученные нами в ходе исследования, могут быть использованы в дальнейшем для разработки возможных путей развития финансовой системы РФ и предположений по её укреплению.





