Задачи на применение дифференциальных уравнений

Аннотация. В различных областях человеческой деятельности возникает большое число задач, решение которых сводится к дифференциальным уравнениям. Пусть происходит некоторый процесс, например, физический, биологический или химический. Нас интересует определённая функциональная характеристика этого процесса, например, закон изменения температуры, давления или массы с течением времени. Надо отметить, что разные по содержанию задачи приводятся к одинаковым или сходным дифференциальным уравнениям. Это будет видно из рассмотренных ниже примеров.

Ключевые слова: обыкновенные дифференциальные уравнения, общее решение, начальное условие, интегралы по частям, сила.

Пример 1. Ракета с начальной массой m₀ кг взлетает с поверхности Земли в вертикальном направлении. Газы, образованные сгоранием топлива, выбрасываются постоянными долями массы  в единицу времени и с постоянной скоростью  , где   и >0. Найти скорость движения ракеты и расстояние, пройденное за время t.

Решение. Движение ракеты происходит путём выброса струи горящего газа с определённой скоростью относительно ракеты. Ракета несёт с собой топливо, которое составляет главную часть переменной массы ракеты. Поэтому движение ракеты должны рассматривать как движение тела с переменной массой.

Согласно второму закону динамики изменение количества движения прямо пропорционально движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Если Q – количество движения тела с массой  m,  F – действующая сила,  – скорость движения тела, то в момент времени  t

Пусть  m=m(t) – масса ракеты в любой момент времени  t  после начала движения,    – её скорость относительно Земли в момент времени  t,  F₁ – внешняя сила, действующая на ракету, F₂  – реактивная сила, направленная по движению ракеты и возникающая за счёт выбросов газов из сопла ракеты. Тогда суммарная сила    и равенство (4) принимает вид 

Реактивная сила    определяется за счёт изменения количества движения убывающей массы. Пусть  – убыль  массы за время  . Масса   имеет скорость , т.е. скорость –  относительно ракеты. Тогда количество движения убывающей массы    равно  . По условию скорость  постоянная, поэтому

Подставляя (3) в равенство (2), получаем дифференциальное уравнение движения ракеты

По условию задачи из ракеты выбрасывается газ массой  за единицу времени, тогда за время  t – масса  . Тогда масса    ракеты, спустя время t, составит

где   – начальное  значение массы ракеты, т.е. . Скорость газа  относительно ракеты известна и равна . Внешняя сила

 – ускорение свободного падения. С учётом (5), (6) и значения , уравнение (4) принимает вид

или

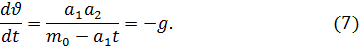
Интегрируя дифференциальное уравнение (7), найдём его общее решение

Пусть . Тогда из (8) имеем  и с учётом этого значения  соотношение (8) примет вид

Полагая в (9)  и интегрируя полученное уравнение, получим

Интегрируя по частям, вычислим последний интеграл:

Тогда, подставляя (11) в (10) и учитывая начальное условие , найдём искомый закон движения ракеты

Таким образом, на основании формул (9) и (12) в любой момент времени   можем определить скорость и высоту подъёма ракеты.

Пример 2(Химическая реакция). В результате химической реакции между жидкими веществами X и Y образуется новое вещество Z. Найти количество вещества Z в любой момент времени после начала реакции, если: а) в момент начала реакции количество веществ X и Y равно соответственно x и y литрам; б) температура в процессе реакции не меняется; в) из каждых m литров вещества X и n литров вещества Y образуется m+n вещества Z.

Решение. Предварительно напомним, что скорость, с которой образуется новое вещество Z, называется скоростью реакции. Действующая масса или концентрация реагирующего вещества определяется количеством молей этого вещества в единице объема.

 Одним из основных законов теории химических реакций является закон действующих масс, согласно которому скорость химической реакции при постоянной температуре прямо пропорциональна произведению концентраций веществ, участвующих в данный момент времени в реакции.

Пусть -количество вещества Z через время t после начала реакции. Тогда  скорость образования вещества Z, т.е. скорость реакции. Из условий задачи следует, что к моменту времени t в химическую реакцию вступило  литров вещества X и  литров вещества Y. Тогда к указанному моменту осталось   литров вещества X и  литров вещества Y. На основании закона действующих масс приходим к дифференциальному уравнению

которое можно переписать в следующем виде:

где 

Разделяя переменные в уравнении (13), получим

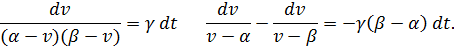
Интегрируя последнее уравнение, имеем

     где  - произвольная постоянная.

Отсюда

Из начального условия  находим . Тогда из (14) получим

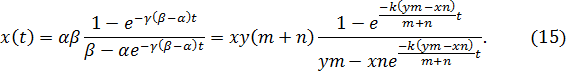
Допустим, что , тогда из формулы (15) следует, что  при . Если , то  при . Если , то и  и уравнение (13) принимает вид

Снова разделяя в (16) переменные и интегрируя, получим

Из условия  и соотношения (17) найдем значение . Тогда равенство а (17) с учетом значения , примет вид

Отсюда  при .