РОЛЬ СКИН ЭФФЕКТА ПРИ ПРОХОЖДЕНИИ ИМПУЛЬСА ТОКА ПО ПРОВОДНИКУ И УЧАСТИЕ ЕГО В ЭЛЕКТРОПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ МЕТАЛЛА
Конференция: CCLXXVII Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Физико-математические науки

CCLXXVII Студенческая международная научно-практическая конференция «Молодежный научный форум»
РОЛЬ СКИН ЭФФЕКТА ПРИ ПРОХОЖДЕНИИ ИМПУЛЬСА ТОКА ПО ПРОВОДНИКУ И УЧАСТИЕ ЕГО В ЭЛЕКТРОПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ МЕТАЛЛА
Введение
Импульсы тока, пропускаемого через проводник во время его деформации, могут, вызывать пинч-эффект (ПЭ) и скин-эффект (СЭ).
Впервые это явление было описано в 1885–1886 гг. английским физиком О. Хевисайтом, спустя примерно 30 лет в XIX веке после открытия Томсоном эффекта смещения зоны нагретости металла в направлении действия тока. Согласно представлениям О. Хевисайта, вихревые токи вытесняются из объёма на поверхность проводника, поскольку на оси проводника они текут против основного тока I или вектора его плотности Jm, а на поверхности – в том же направлении, как показано на схеме Рис.1.
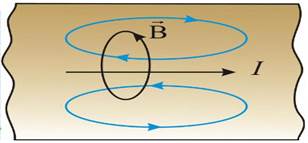
Рисунок 1. Физическая картина возникновения
Явление назвали скин-эффектом от английского слова skin – кожа, или оболочка. Таким образом, СЭ заключается в выходе тока на поверхность проводника на переднем фронте и уходе с поверхности на заднем фронте основного импульса тока. Оба фронта имеют продолжительность примерно 10-5 сек. Это на порядок величины меньше длительности основного импульса тока (около 10-4 сек. в большую сторону). СЭ эквивалентен переменному току умеренных частот. Некоторым результатом СЭ может быть ослабление собственного магнитного поля (МП) основного тока по мере оттеснения линий тока вглубь проводника против вихревого электрического поля и тока. Не исключено возникновение некоторого термического разупрочнения материала проводника, несмотря на кратковременность действия основного тока. СЭ, таким образом, обусловлен действием вихревых токов умеренных частот при прохождении электромагнитной волны основного импульса тока на обоих его фронтах. Небольшая часть энергии импульса при этом преобразуется в теплоту. В результате СЭ может происходить также некоторое уменьшение напряженности электрического поля E и индукции B собственного магнитного поля тока. В какой-то мере по этим же причинам уменьшается плотность тока Jm, по распределению его линий в глубине проводника. Но это не делает СЭ существенным эффектом в ЭПЭ двойникованием [4].
Согласно уравнению Максвелла, касающегося закона электромагнитной индукции Фарадея, ![]() дВ/дt, изменение магнитной индукции В во времени дВ/дt порождает вихревое электрическое поле Е,
дВ/дt, изменение магнитной индукции В во времени дВ/дt порождает вихревое электрическое поле Е,
где с – скорость света. В-индукция собственного магнитного поля импульса тока. Амплитуда электромагнитного изменяется по экспоненте и пропорциональна коэффициенту затухания ![]() где, частота ЭМ поля
где, частота ЭМ поля ![]() , магнитная проницаемость материала
, магнитная проницаемость материала ![]() и магнитная постоянной μ0 = 4π ·10−7 Гн/м, проводимость материала
и магнитная постоянной μ0 = 4π ·10−7 Гн/м, проводимость материала ![]() , обратная величина удельного электрического сопротивления, равного для висмута 1,210-6 Ом·м при +17,5 °C. От указанных функций и параметров тока зависит величина мощности, рассеиваемой в единице объема проводника.
, обратная величина удельного электрического сопротивления, равного для висмута 1,210-6 Ом·м при +17,5 °C. От указанных функций и параметров тока зависит величина мощности, рассеиваемой в единице объема проводника.

Рисунок 2. Микрофотография двойников на плоскости спайности монокристаллов висмута, х 530. Отпечаток слева получен при нагрузке на индентор 10г. Отпечаток справа ‒ при той же нагрузке на индентор, но во время деформации через кристалл пропускался импульс тока плотностью 600 А/мм2
За величину скин-слоя L принято считать расстояние от поверхности в глубину материала, где амплитуда электромагнитных колебаний уменьшается в е раз. Амплитуды напряженностей электрического и магнитных полей затухают по экспоненциальному закону. Величина скин-слоя определяется выражением L=1/![]() c иравна L=1,5 мм с учетом коэффициента затухания
c иравна L=1,5 мм с учетом коэффициента затухания ![]() и частотой
и частотой ![]() вихревого тока [3]. Сравним полученную величину скин слоя с глубиной проникновения двойника в кристалл по данным на поперечных шлифах. Двойники распространяются вглубь кристалла на расстояния равные распространению двойника на плоскости спайности (111) порядка не более (0,3‒0,4)10-3 мм. Следовательно, теоретически определённая глубина скин-слоя L во много раз превышает размеры зоны, охваченной двойникованием. Отсюда можно сделать вывод–скин эффект в данном случае является второстепенным фактором и процессом. Он действует на фронтах основного импульса тока, в принципе, не может вносить существенного вклада в ЭПЭ двойниковании.
вихревого тока [3]. Сравним полученную величину скин слоя с глубиной проникновения двойника в кристалл по данным на поперечных шлифах. Двойники распространяются вглубь кристалла на расстояния равные распространению двойника на плоскости спайности (111) порядка не более (0,3‒0,4)10-3 мм. Следовательно, теоретически определённая глубина скин-слоя L во много раз превышает размеры зоны, охваченной двойникованием. Отсюда можно сделать вывод–скин эффект в данном случае является второстепенным фактором и процессом. Он действует на фронтах основного импульса тока, в принципе, не может вносить существенного вклада в ЭПЭ двойниковании.
2. Скин-эффект, сопутствующий электродинамическому пинч- эффекту
В рассматриваемых теориях особое место уделяется электродинамическому действию тока на деформируемый металл. Это объясняется тем, что ЭПЭ и явление ЭПДМ были обнаружены при действии на деформируемые образцы импульсным током, которому свойственно электродинамическое пинч-действие (от английского слова pinch-щипок или стеснение). Кроме того, есть основание считать и имеются экспериментальные доказательства того, что электродинамическое действие импульсного тока является одним из основных эффектов влияния тока на пластическую деформацию металла в кооперативном явлении ЭПДМ. Физическая картина электродинамического пинч-эффекта заключается, как известно, в том, что под влиянием собственного магнитного поля тока, которое кольцевыми линиями охватывает проводник, происходит оттеснение электронов проводимости и линий тока от поверхности вглубь металла. Происходящая при этом поляризация электронной системы металла в приповерхностных областях приводит к возникновению поперечного электрического поля Холла, которое препятствует дальнейшему сжатию электронной плазмы металла и становится причиной появления значительного давления собственного магнитного поля тока на деформируемый проводник в радиальном направлении.
Первоначальной силой и первопричиной возникновения пинч-эффекта является сила Лоренца, которая действует со стороны собственного магнитного поля тока на движущиеся с дрейфовыми скоростями vе электроны проводимости или движущуюся электронную плазму металла с отжиманием ее к оси образца. Возникающие при этом значительные механические напряжения обусловлены действием поперечного поля Холла на ионный остов решетки. Указанные напряжения первоначально действуют в радиальном направлении и возникают с частотой следования импульсов тока. Создается вибрация кристаллической решетки за счет упругих колебаний ее узлов по типу ультразвуковых. Это приводит в конечном итоге к интенсификации пластической деформации металла через решеточную подсистему. Величина пинч-эффекта при одной и той же плотности импульсного тока различна для всех металлов в силу различий в скоростях диффузии магнитного поля вглубь образцов. Поэтому возникающие механические напряжения от пинч-эффекта различны для металлов из разных групп таблицы Менделеева. Скорость диффузии магнитного поля вглубь металла, таким образом, существенным образом влияет на величину и интенсивность пинч-действия импульсного тока. Скорость диффузии магнитного поля определяет также величину скин-эффекта, в известной мере противоположного пинч-эффекту и характеризующего неоднородность распределения плотности тока в поперечном сечении проводника. Прохождение импульса тока по проводнику начинается с поверхностных слоев, а объемный ток запаздывает к полному току на величину времени τ затухания магнитного поля в образце, которое определяется по формуле
τ = 4πλR2 / c2μ
где λ – проводимость металла; μ – геометрический фактор, равный 3,8; с –скорость света; R – радиус образца. Из последней формулы следует, что с понижением температуры, вследствие роста λ динамический пинч-эффект может усиливаться. Поэтому ЭПДМ целесообразно проводить без большого нагрева металла, что было неоднократно подтверждено в экспериментах.
Другой практический вывод касается скин-эффекта, сопутствующего ЭПДМ и в известной мере определяющему величину динамического пинч-эффекта во время ЭПДМ. Дело в том, что скин-эффект, величина которого зависит от скорости диффузии магнитного поля внутрь металла, определяет крутизну фронтов импульсов тока, проходящих по металлу во время ЭПДМ. Этот эффект может вызвать кратковременные существенные повышения плотности тока на поверхности проводника, повторяющиеся при каждом очередном импульсе тока, если отношение длительности фронтов импульсов
tf ко времени затухания магнитного поля τ сделать меньшим 2 , т. е. создать условия для выполнения следующего неравенства:
n = tf / τ < 2,что может быть полезным для ЭПДМ волочением проволоки с целью снижения трения волоке.
Учитывая то, что параметр τ зависит исключительно от природы металла, а параметр tf может зависеть также от условий эксперимента и режимов ЭПДМ, в частности, от индуктивности проводов, подводящих ток от генератора к зоне деформации металла во время ЭПДМ, эффективное управление скин-эффектом с соблюдением приведенного неравенства можно осуществлять варьированием параметром длительности переднего фронта импульсов tf в сторону его уменьшения.
Указанное обстоятельство необходимо учитывать проектировщикам и изготовителям генераторов импульсного тока для целей ЭПДМ, закладывая в их конструкции и схемы возможность варьирования параметром tf в широких пределах, например, в пределах от 10 -6 до 10-5 сек., т. е. не менее, чем на порядок величины. Важно отметить, что в статическом пределе сдвиговые напряжения, создаваемые пинч-эффектом, почти постоянны по сечению проводника и определяются по формуле
σp = кJm2 R2 / c2,
где к –определяемый формой проводника и действующими системами скольжения дислокаций коэффициентом Пуассона, равный 0,5.
В силу квадратичной зависимости σp от плотности тока Jm и от радиуса образца R (в общем случае – поперечного его размера) в определенных условиях и при специальных режимах тока динамический пинч-эффект может стать доминирующим в суммарном эффекте действия тока при ЭПДМ.





