Учебно-исследовательские карты как средство организации самостоятельной работы с учебником на уроках геометрии в 7 классе

Из всех предметов математического цикла, которые изучаются в средней школе, геометрия обладает уникальными возможностями для развития мышления детей. Наглядность материала геометрии облегчает школьникам деятельность по открытию новых математических фактов и установлению взаимосвязей между ними.

Изучение геометрии помогает в овладении искусством построения правильного логического анализа ситуаций, развивает умение отличать неизвестное от известного и доказанное от недоказанного, определять различные понятия и работать с основными определениями, классифицировать, анализировать, выдвигать и обосновывать гипотезы, пользоваться аналогиями.

В 7 классе начинается изучение систематического курса геометрии. Основная сложность данного этапа заключена в том, что при изложении геометрического материала учащиеся впервые встречаются с большим количеством определений, аксиом, теорем, здесь появляются первые строго построенные доказательства геометрических фактов.

Материал, который изучается в 7 классе, находит широкое применение в последующем курсе геометрии. Отсюда и вытекает необходимость того, чтобы знания по геометрии, полученные школьниками в 7 классе, были глубокими, прочными и осмысленными. Достижение такого результата возможно путем вовлечения учащихся в самостоятельную, экспериментальную, исследовательскую деятельность. Средством организации указанных видов деятельности являются учебно-исследовательские карты.

Учебно-исследовательские карты могут быть направлены на самостоятельное изучение теоретического материала по учебнику, при этом учитель выполняет роль координатора и помощника.

Учебно-исследовательская карта состоит из системы заданий, выполнение которых включает элементы исследовательской деятельности: наблюдение, создание гипотезы, доказательство или опровержение гипотезы. Такой дидактический материал может быть предложен как для групповой, так и для индивидуальной работы учащихся.

Приведем пример разработанной нами учебно-исследовательской карты, предназначенной для изучения нового материала по учебнику [1]. Мы приводим заполненный вариант учебно-исследовательской карты, при этом возможные ответы ученика выделены курсивом.

Тема «Медианы, биссектрисы и высоты треугольника»

1.  Изучите п.17 (стр. 33) и впишите пропущенные слова.

·     Определение

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

·     Определение

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

·     Определение

Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону называется высотой треугольника.

2.  С помощью чертежных инструментов выясните, какой из отрезков AH, AM и AP является медианой, биссектрисой, а какой высотой треугольника ABC.

Решение:

1.  Медианой треугольника ABC является отрезок АР, так как точка Р является серединой стороны ВС.

2.  Биссектрисой треугольника ABC является отрезок АН, так как луч АН является биссектрисой угла BАC треугольника ABC.

3.  Высотой треугольника ABC является отрезок АМ, так как он является перпендикуляром к стороне ВС.

3. Соотнесите.

4.  Изучите свойства медианы, биссектрисы и высоты треугольника (стр. 34) и выполните задание.

Три отрезка в каждом треугольнике пересекаются в одной точке. Выберите рисунок, на котором изображены медианы, биссектрисы и высоты треугольника. Сформулируйте свойство в правом столбце таблицы.

5.  Решите следующие задачи:

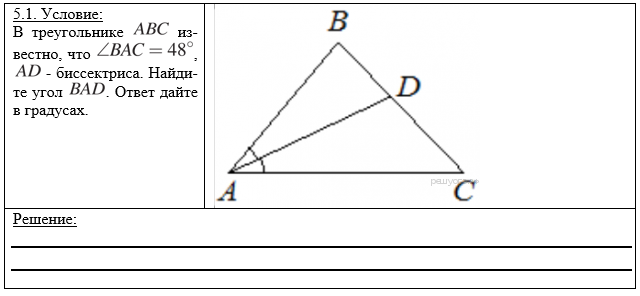
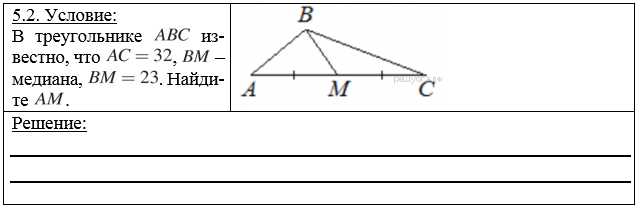
5.3. На медиане LD треугольника OLR отмечена точка N. Докажите, что ND является медианой треугольника ONR.

Доказательство:

Медианой треугольника является отрезок, который проведён от вершины треугольника (обведи нужное)

·     к серединной точке противоположной стороны треугольника

·     перпендикулярно стороне треугольника

1)  У данного треугольника OLR и треугольника ONR сторона OR общая.

2)  Так как в треугольнике ONR отрезок ND проведён от вершины N к середине стороны OR, то является медианой этого треугольника.Конец формы

6.  С помощью чертежных инструментов проведите в треугольнике МКР а) биссектрису из вершины Р; б) Высоту из вершины К; в) медиану из вершины М.

Применяя подобную форму работу на уроке, мы наблюдали:

·     повышение познавательного интереса к геометрии;

·     развитие умения самостоятельно добывать знания;

·     развитие коммуникативных умений.

Заметим, что согласно стандартам второго поколения, учителю нужно помочь ребенку научиться учиться, и дидактическое обеспечение в виде учебно-исследовательских карт позволяет достичь указанной цели.