СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ НА УРОКЕ ОДНОЙ ЗАДАЧИ
Конференция: LVIII Студенческая международная научно-практическая конференция «Гуманитарные науки. Студенческий научный форум»
Секция: Педагогика
лауреатов
участников
лауреатов


участников



LVIII Студенческая международная научно-практическая конференция «Гуманитарные науки. Студенческий научный форум»
СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ НА УРОКЕ ОДНОЙ ЗАДАЧИ
Аннотация. В процессе работы учитель намного часто сталкивается с такими фактами. Как когда ученик не умеет решать квадратные уравнения вообще. Но есть ребята, которые решают. Но только одним способом, и то по формуле с нахождением дискриминанта. И при таких знаниях урок математики проходит не очень продуктивно. Главная задача учителя – научить школьников решать квадратные уравнения по первой формуле. И только тогда, когда учащиеся в совершенстве смогут применять первую формулу для решения квадратных уравнений, последовательно вводятся вторая, третья и четвертая формулы. Учителю важно показать эффективность применения этих формул. В результате такого подхода к обучению решению квадратных уравнений и предлагаемым способам тренингов большинство учеников хорошо запомнят все четыре способа, а первую формулу будут знать все без исключения учащиеся.
Ключевые слова: Уравнения, квадратные уравнения, дискриминант, теорема Виета, способ «переброски».
На уроке решения одной задачи ученик услышит разные рассуждения, мнения, увидит различные приемы решения. Кроме того, у учителя уменьшается возможность навязать свой способ рассуждения, значит, уменьшается потребность учить по шаблону «делай как я», а у ученика, наоборот, появляется возможность действовать так, как он хочет. Таким образом, учитель формирует личность, способную думать, отстаивать свое мнение, находить выход из создавшейся ситуации, а в перспективе разбираться в жизни, в людях[2].
Уроки одной задачи не оставляют равнодушными ни одного ученика. Возрастает мотивация обучения математике, улучшаются результаты самостоятельных и контрольных работ.
Стандартные способы решения квадратных уравнений из школьной программы:
- Разложение левой части уравнения на множители.
- Метод выделения полного квадрата.
- Решение квадратных уравнений по формуле.
- Графическое решение квадратного уравнения.
- Решение уравнений с использованием теоремы Виета.
Остановимся подробнее на решение приведенных и не приведенных квадратных уравнений по теореме Виета.
Напомним, что для решения приведенных квадратных уравнений достаточно найти два числа такие, произведение которых равно свободному члену, а сумма - второму коэффициенту с противоположным знаком. Пример:
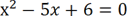
Нужно найти числа, произведение которых равно 6, а сумма 5.
Такими числами будут 3 и 2.
Ответ: X1= 2, X2= 3.
Но можно использовать этот способ и для уравнений с первым коэффициентом не равным единице. Пример:
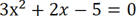
Берём первый коэффициент и умножаем его на свободный член:
![]()
Корнями этого уравнения будут числа, произведение которых равно -15, а сумма равна -2. Эти числа -5 и 3.
Чтобы найти корни исходного уравнения, полученные корни делим на первый коэффициент.
Ответ: x1= -5/3, x2= 1.
6. Решение уравнений способом "переброски". Рассмотрим квадратное уравнение:
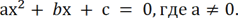
Умножая обе его части на а, получаем уравнение:
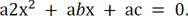
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению y2 + by + ас = 0, равносильному данному.
Его корни Y1 и Y2. Найдем с помощью теоремы Виета.
Окончательно получаем
x1= y1/a, x2 = y2/a.
При этом способе коэффициент a умножается на свободный член, как бы "перебрасывается" к нему, поэтому его называют способом "переброски". Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат[4]. Пример:

"Перебросим" коэффициент 2 к свободному члену и сделав замену получим уравнение
![]()
Согласно обратной теореме Виета ![]()
![]() .
.
Ответ: ![]()
7. Свойства коэффициентов квадратного уравнения. Пусть дано квадратное уравнение:
![]() .
.
Если a + b + c = 0 (т.е. сумма коэффициентов уравнения равна нулю), то x1 = 1.
Если: ![]()
Пример. ![]()
Так как а + b + с = 0 (345 - 137 - 208 = 0), то x1 = 1, x2= -208/345.
Ответ: x1 = 1, x2= -208/345.
Для примера
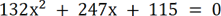
Т.к.
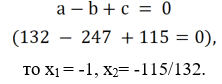
Ответ: x1 = -1, x2= -115/132.
Есть другие свойства коэффициентов квадратного уравнения. Но их применение более сложное.
8. Решение уравнений с использованием теоремы Безу. Теорема Безу. Остаток от деления многочлена P(x) на двучлен x - α равен P(α) (т.е. значению P(x) при x = α). Если число α является корнем многочлена P(x), то этот многочлен делится на x -α без остатка[3].
Пример.
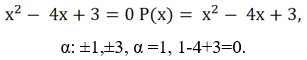
Разделим Р(x) на
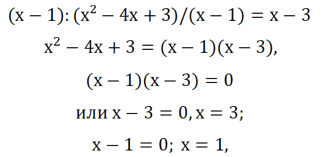
Ответ: x1=2, x2=3.
Как раз, изучив все найденные способы решения квадратных уравнений, мы можем дать советы своим одноклассникам, что есть не только стандартных способы решения, но и решения способом переброски и решение уравнений по свойству коэффициентов, так как они более понятны.

