Анализ методов обнаружения объектов

В работе представлен краткий обзор некоторых методов обработки и поиска объектов на изображении. Цифровая обработка изображений осуществлялась с помощью Image Processing Toolbox - пакета расширения MATLAB.

Предобработка изображения

Прежде чем приступать к обнаружению объектов на изображении необходимо подготовить изображение к обработке, т.е. выполнить предобработку.

К этапу предобработки можно отнести следующие операции над изображением такие, как перевод полноцветного изображения в полутоновое, бинаризация изображения, контрастирование изображения, повышение резкости изображения, сегментация,  фильтрация и т.п.

Сегментация делит изображение на составные части и объекты. Степень детализации этого деления зависит от решаемой задачи. Иными словами, сегментацию следует остановить, когда интересующие объекты уже выделены или изолированы.

Сегментация сложных изображений является весьма нетривиальной задачей обработки изображений. Точность сегментации во многом определяет успех конечных компьютеризованных процедур анализа изображений.

Как правило, алгоритмы сегментации монохромных изображений основаны на одном из двух базовых свойствах яркости изображения: разрывности и однородности. В первом случае подход состоит в разбиении изображения на части исходя из резких перепадов значений яркости, которые происходят, например, на границах объектов. Вторая группа методов осуществляет разделение изображений на области, однородные в смысле определенных, заранее заданных критериев [3].

Методы нахождения краев являются едва ли не самыми важными при обнаружении значимых разрывов яркости на изображении. При поиске таких перепадов используются производные первого и второго порядка.  Основная идея обнаружения перепадов базируется на поиске мест изображения, где яркость меняется быстро, с помощью следующих критериев:

1) найти места, где первая производная яркости превосходит по модулю некоторый заранее заданный порог;

2) найти места, где вторые производные яркости имеют пересечения нулевого уровня.

Рассмотрим наиболее распространенные  детекторы выделения краев на примере рис. 1.

Рисунок 1. Исходное изображение

1.  Детектор Собеля для обнаружения перепадов использует маски вида:

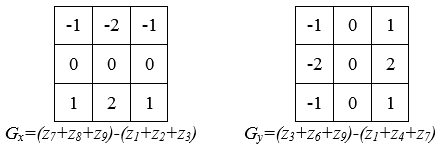
для численного приближения производных G_x и G_y. Другими словами, градиент в центральной точке окрестности вычисляется по формуле:

Мы скажем, что пиксель с координатами (x, y) является пикселем перепада, если для него g ≥ T, где T – это выбранный порог.

a) b)

Рисунок 2. Результаты обнаружения краев детектором Собеля при автоматическом определении порога (a) и заданном значение порога =0,1 (b)

2. Детектор Превитта использует маску вида:

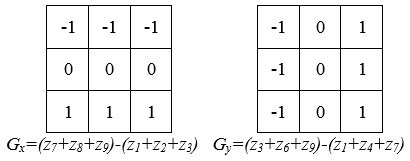
для численного приближения производных G_x и G_y.

a) b)

Рисунок 3. Результаты обнаружения краев детектором Превитта при автоматическом определении порога (a) и заданном значение порога =0,1 (b)

3. Детектор Робертса основан на маске вида:

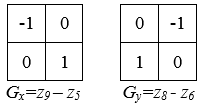
для приближения производных G_x и G_y.

a) b)

Рисунок 4.  Результаты обнаружения краев детектором Робертса при автоматическом определении порога (a) и заданном значение порога =0,1 (b)

4. Детектор лапласиан гауссиана

Рассмотрим функцию Гаусса:

где  r²=x²+y², а ơ – это стандартное отклонение. Свертка этой сглаживающей функции с изображением приводит к его расфокусировке, степень которой определяется значением ơ. Лапласиан функции Гаусса (вторая производная по r)  равен:

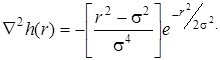
Эту  функцию принято называть лапласианом гауссиана. Поскольку взятие второй производной является линейной операцией, то свертка (фильтрация) изображений с Δ²h(r) – это то же самое, что свертка функции со сглаживающей функцией, а затем применение  оператора Лапласа к результату. В этих действиях проявляются  ключевые свойства этого детектора. Свертка изображений Δ²h(r)  даст два эффекта: она сглаживает изображение (сокращает шум) и вычисляет лапласиан, что выявляем сдвоенные края на изображении.

a) b)

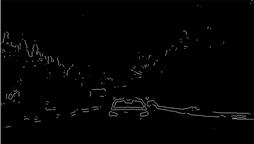
Рисунок 5. Результаты обнаружения краев детектором лапласиан гауссиана при автоматическом определении порога и значением отклонения по умолчанию = 2 (a) и заданном значение порога = 0,0017 и отклонения = 3 (b)

5. Детектор Кани

Этот метод кратко можно описать следующим образом:

1) изображение сглаживается гауссовым фильтром с заданным стандартным отклонением для сокращения шума;

2) в каждой точке вычисляется градиент и направление края α(x,y)=arctg(G_y/G_x). Точки перепада определяются как точки локального максимума градиента;

3) точки перепада вызывают рост гребней на изображении модуля градиента. Затем алгоритм отслеживает верх этих гребней и присваивает нулевое значение точкам, которые не лежат на гребне. В результате на выходе строится тонкая линия, а весь этот процесс называется немаксимальным подавлением. Затем пиксели гребня повергаются пороговой обработке с использованием двух порогов T1 и T2, причем T1<T2. Пиксели гребня, величина которых больше T2, называют “сильными”, а пиксели, значения которых попадают в интервал [T1, T2], называются “слабыми”.

4) наконец, алгоритм совершает соединение, добавляя к сильным пикселям слабые.

a) b)

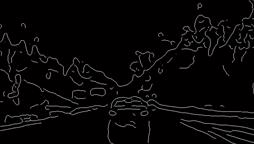
Рисунок 6. Результаты обнаружения краев детектором Канни при автоматическом определении порога и значением отклонения по умолчанию =1 (a) и заданном значение порога =[0,04 0,07] и отклонения =3 (b)

На основе полученных результатов можно сделать вывод, что при выделении границ на изображении наиболее универсальным является детектор Собеля.

Понятие линейной пространственной фильтрации тесно связано с преобразованием Фурье при обработке сигналов в частотной области. Механизм линейной пространственной фильтрации проиллюстрирован на рис. 7.

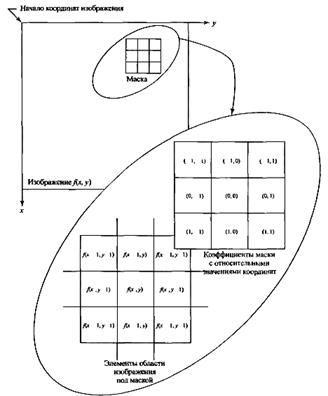
Рисунок 7. Механизм линейной пространственной фильтрации

Процесс заключается в перемещении центра фильтрующей маски w от точки к точке изображения f. В каждой точке (x,y) откликом является сумма произведений коэффициентов фильтра и соответствующих пикселов окрестности, называемых фильтрующей маской. Т.о. на изображении подавляются шумы.

Рассмотрим результаты линейной пространственной фильтрации, проведенной над рис. 1.

В результате применения фильтра усреднения мы получаем размытое изображение (рис. 8).

h = ones(5) / 25;%фильтр усреднения

I2 = imfilter(double(I),h); %фильтрация делается м-дом корреляции, границы изобр расширяются значением Р=0

Рисунок 8. Результаты применения фильтра усреднения

gr=imfilter(double(I),w,'replicate');%фильтрация делается м-дом корреляции, размер изобр увеличивается повторением величин на его боковых границах

Рисунок 9. Результаты фильтрации методом корреляции

В данном случае (рис. 9) мы видим, что расширение границ (из-за большой маски) не происходит с помощью белых или черных пикселов.

grc=imfilter(double(I),w,'conv','replicate');%фильтрация делается м-дом свертки

Рисунок 10. Результаты фильтрации методом свертки

% возвращает маску u фильтра, повышающего резкость изображения

u = fspecial('unsharp');%u=[-0.1667 -0.6667 -0.1667;-0.6667    4.3333   -0.6667;-0.1667 -0.6667 -0.1667]

I2 = imfilter(I,u);

Рисунок 11. Результаты применения фильтра, повышающего резкость изображения

Метод межкадровой разности

Вычисление межкадровой разности является распространенным методом первичного обнаружения движения, после которого можно определить  присутствует ли в потоке данных движущийся объект.

Алгоритм вычисления межкадровой разности выглядит следующим образом:

1. На вход алгоритма поступают два видеокадра.

2. Производится вычисление попиксельных межкадровых разностей по следующей схеме:

3. Разность сравнивается с заданным порогом Т.

4. В результате сравнения формируется двоичная маска вида:

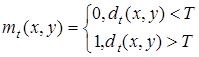
где – значение t-го элемента маски, Т – порог сравнения.

Реализованный код алгоритма представлен в прил. 2.

Результаты обработки видео данным методом представлены ниже на рис. 12:

Рисунок 12. Результаты обработки видео методом межкадровой разности

Данный метод подходит для задачи видеонаблюдения за объектом - так называемых детекторов движения, например, для создания охранных систем или систем наблюдения.

Кластеризация методом k-средних

Метод k-средних – это метод кластерного анализа, целью которого является разделение m наблюдений (из пространства) на k кластеров, при этом каждое наблюдение относится к тому кластеру, к центу (центроиду) которого оно ближе всего.

В качестве меры близости используется Евклидово расстояние:

Итак, рассмотрим ряд наблюдений (x⁽¹⁾, x⁽²⁾, …, x^(m)), x^(j) ͼ Rⁿ .

Метод k-средних разделяет m наблюдений на k групп (или кластеров) (k ≤ m) S={S₁,S₂, …, S_k}, чтобы минимизировать суммарное квадратичное отклонение точек кластеров от центроидов этих кластеров:

Алгоритм:

Итак, если мера близости до центроида определена, то разбиение объектов на кластеры сводится к определению центроидов этих кластеров. Число кластеров k задается исследователем заранее.

Рассмотрим первоначальный набор k средних (центроидов)  в кластерах . На первом этапе центроиды кластеров выбираются случайно или по определенному правилу (например, выбрать центроиды, максимизирующие начальные расстояния между кластерами).

Относим наблюдения к тем кластерам, чье среднее (центроид) к ним ближе всего. Каждое наблюдение принадлежит только к одному кластеру, даже если его можно отнести к двум и более кластерам.

Затем центроид каждого i-го кластера перевычисляется по следующему правилу:

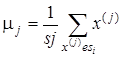
Таким образом, алгоритм k-средних заключается в перевычислении на каждом шаге центроида для каждого кластера, полученного на предыдущем шаге.

Алгоритм останавливается, когда значения центроида не меняются.

Однако неправильный выбор первоначального числа кластеров k может привести к некорректным результатам. Именно поэтому при использовании метода k-средних важно сначала провести проверку подходящего числа кластеров для данного набора данных.

Код программы данного метода представлен в прил. 3. Результаты выполнения кластеризации приведены ниже (рис. 13 и рис 14):

a) b) c) d)

Рисунок 13. Результаты кластеризации методом к-средних; a) – исходное изображение; b) – объекты в кластере 1; c) – объекты в кластере 2; d) – объекты в кластере 3

Рисунок 14. Результаты кластеризации методом к-средних

Данный метод может подойти при решении задач, связанных с обнаружением объектов определенного цвета, например, для распознавания цвета загоревшейся лампы светофора.

Существенным недостатком данного метода является то, что данный метод “медленный”, так, например, кластеризация, результаты которой представлены на рис. 13, длилась 37,6669 с.

Метод Оцу

Метод Оцу — это алгоритм вычисления порога бинаризации для изображения, используемый в области компьютерного распознавания образов и обработки изображений.

Алгоритм позволяет разделить пиксели двух классов (“полезные” и “фоновые”), рассчитывая такой порог, чтобы внутриклассовая дисперсия была минимальной.

Данный метод использует гистограмму изображения для расчета порога, гистограммой в этом случае является набор битов, каждый из которых характеризует количество попаданий в него элементов выборки. В нашем случае выборка — это пиксели различной яркости (от 0 до 255).

В методе Оцу ищется порог,  который уменьшает дисперсию внутри класса, которая в свою очередь определяется как взвешенная сумма дисперсий двух классов:

где веса ωi — это вероятности двух классов, разделенных порогом t, σ_i — дисперсия этих классов.

В своей работе Оцу показал, что минимизация внутриклассовой дисперсии равносильна максимизации дисперсии между классами:

Данная идея привела к эффективному алгоритму:

1. Вычислить гистограмму и вероятность для каждого уровня интенсивности.

2. Вычислить начальные значения для ω_i(0) и μ_i(0).

3. Для каждого значения порога от t = 1 .. до максимальной интенсивности:

- обновить  и вычислить σ²_b(t);

- если σ_b(t) больше, чем имеющееся, то запоминаем σ_b и значение порога t.

4. Искомый порог соответствует максимуму σ²_b(t).

Результаты обработки данным методом приведены ниже (рис. 15 и рис. 17):

Рисунок 15. Результаты обработки методом Оцу

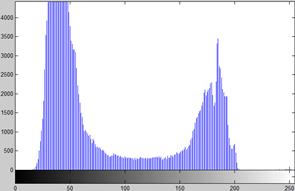
Рисунок 16. Гистограмма изображения, рассчитанный порог = 126

Рисунок 17. Результаты обработки видео методом Оцу

На рис. 17 представлены результаты обработки видео длительностью 8 секунд, кадры обрабатывались с интервалом в 2 секунды. Обработка заняла 1,1120 с.

Но недостатком этого метода является не точное обнаружение объекта в темное время суток и при неблагоприятных погодных условиях (рис. 18).

Рисунок 18. Результаты обработки видео методом Оцу