НЕКОТОРЫЕ ПРИКЛАДНЫЕ АСПЕКТЫ ТРИГОНОМЕТРИИ
Журнал: Научный журнал «Студенческий форум» выпуск №41(220)
Рубрика: Физико-математические науки

Научный журнал «Студенческий форум» выпуск №41(220)
НЕКОТОРЫЕ ПРИКЛАДНЫЕ АСПЕКТЫ ТРИГОНОМЕТРИИ
На сегодняшний день в системе российского образования накоплен огромный опыт в изучении тригонометрии, имеется большая база методических разработок, различные подходы и системы учебных заданий, но, несмотря на все это, на выходе мы получаем выпускников школы, которые имеют слабые знания в тригонометрии и считают этот раздел «дремучим лесом», который наполнен страшными и непонятными формулами. Многие ученики, только начав знакомиться с тригонометрией, сразу отвергают ее и не пытаются понять, не осознают каким практическим применением она обладает.
Тригонометрический материал весьма интересен и специфичен, так как тригонометрия соединяет в себе элементы геометрии и алгебры и применяется во многих областях. Например, тригонометрия или тригонометрические функции используются в астрономии, в морской и воздушной навигации, в теории музыки, в акустике, в физике, в анализе финансовых рынков, в электронике, в теории вероятностей, в биологии, в медицинской визуализации, в архитектуре, в сейсмологии, в картографии, в компьютерной графике и разработке игр и т.д. Это лишь часть того, где применяется тригонометрия.
Рассмотрим некоторые прикладные аспекты тригонометрии.
Раньше всего потребность решения треугольников появилась в астрономии, именно поэтому тригонометрия долгое время изучалась как один из разделов астрономии. Тригонометрию использовали для точного определения времени суток, вычисления положения небесных тел и затмений, расчета расстояния между населенными пунктами, координаты которых были известны. Более того, именно в астрономии впервые были использованы методы сферической тригонометрии, ведь одной из задач астрономии – решение сферических треугольников.
Также, как и в астрономии необходима тригонометрия, так и в физике.
В физике тригонометрия применяется в описании периодических процессов: гармонических и механических колебаний, в оптике, при расчете угла преломления(например, явление радуги), в задачах по баллистике, а также в механике и еще во многих других разделах. Также ярким примером применения тригонометрии в физике является объяснение северного сияния.
Свое применение тригонометрия нашла в биологии и медицине. Одно из основных свойств природы – цикличность многих процессов, которые в ней происходят. Между живыми организмами на Земле и движением небесных тел существует связь. Эта связь описывается биоритмами. Биоритмы – это регулярные изменения биологических процессов. Такая способность к изменениям жизнедеятельности обнаружена почти у всех живых организмов и может наблюдаться как в отдельных клетках, тканях и органах, так и в целых организмах и популяциях.
Существует теория трех ритмов, которая описывает различную активность человека, куда входят физический ритм, эмоциональный ритм и интеллектуальный ритм, все эти ритмы описываются с помощью синусоиды и начинают отсчет в момент рождения человека.
Также с помощью тригонометрии можно описать движение некоторых живых организмов. Например, рыбы в воде двигаются по закону синуса или косинуса, если зафиксировать точку на хвосте, а при плавании тело рыбы принимает форму кривой, которая похожа на график функции тангенса.
В медицине существует формула сердца, которую открыли иранские ученые с помощью тригонометрии. Эта формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров. Также многим людям приходилось делать кардиограмму, но мало кто задумывался о том, что кардиограмма – это график синуса или косинуса.
Тригонометрия в архитектуре и искусстве. Одним из величайших мастеров в архитектуре был Антонио Гауди – испанский архитектор, который создавал фантастические работы. Стиль, в котором творил Гауди, относят к модерну. Модерн – это художественное направление в искусстве, его отличительными особенностями является отказ от прямых линий и углов в пользу более естественных линий. Например, детская школа Гауди в Барселоне (Рис. Рисунок 1. Детская школа Гауди) , где используется поверхность Гауди (Рис. Рисунок 2.).

Рисунок 1. Детская школа Гауди
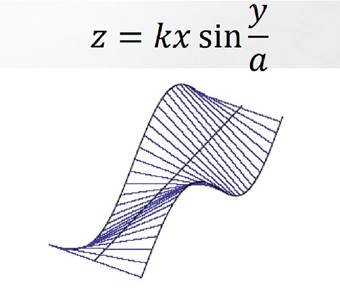
Рисунок 2. Поверхность Гауди
Тригонометрия преодолела длинный и сложный путь развития. Изначально тригонометрия была необходима для измерения углов, но сейчас невозможно представить ни одну сферу жизнедеятельности человека, где бы она не применялась. Тригонометрия тесно связана с явлениями окружающего мира и обладает огромной практической значимостью.

