ОРТОГОНАЛЬНЫЕ ОПЕРАТОРЫ
Журнал: Научный журнал «Студенческий форум» выпуск №18(197)
Рубрика: Физико-математические науки

Научный журнал «Студенческий форум» выпуск №18(197)
ОРТОГОНАЛЬНЫЕ ОПЕРАТОРЫ
Аннотация. Актуальность данной темы состоит в том, что в евклидовом пространстве ортогональные операторы играют важнейшую роль. Он сохраняет скалярное произведение, что в свою очередь означает, что длинны векторов и углы между ними сохраняются. Ортогональные операторы широко используются в геометрии, физике, медицине.
Ключевые слова: ортогональные операторы
Зачем использовать ортогональные операторы, когда обычный подход Слейтера-Кондона, такой как код Коуэна [4, 5], настолько прост в использовании в качестве универсального инструмента? Код Коуэна был благословением для экспериментального физика-атомщика в течение последних 50 лет, и он, без сомнения, будет оставаться таким в течение многих лет, чтобы приходить. Подход ортогонального оператора можно рассматривать как расширение и уточнение обычного подхода подгонки наименьших квадратов (LSF), но он также повышает необходимость поиска физически приемлемых первоначальных оценок для довольно большого числа малых параметров, особенно с неполным спектром. С другой стороны, стабильность параметапо сравнению с изменением или добавлением других является большим преимуществом метода. Рисунок 1 дает четкое представление об этом аспекте [6].
В первой подгонке (слева направо) только параметр eav был разрешен к изменяемым со всеми другими параметрами, зафиксированными на нуле, в то время как в последующих соответствиях параметр, указанный на абсциссе, был added. (b) Значения параметра E av с использованием той же процедуры, что и в (a), но с использованием набора ортогональных эквивалентов.
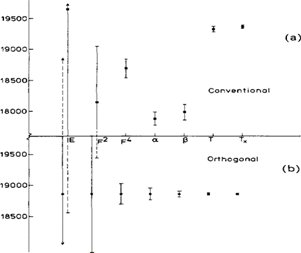
Рисунок 1. (a) Значения параметра Eav в ряде LSF в конфигурации 3d3 в Cr IV
Как обычный, так и ортогональный операторный подходы основаны на полуэмпирическом LSF физических параметров. Среднюю ошибку можно интерпретировать как 'blobsize’, используемую художниками (Сёра и др.) арт-движения 'Пуантилизм'[3]. Они использовали большие двоичные объекты для своих картин и не могли представлять детали меньше, чем капли. Точно так же we не может подробно описать структуры уровней, когда расстояние между уровнями меньше или сопоставимо со средней погрешностью.
Во многих случаях средняя погрешность ортогонального оператора LSF меньше на порядок по величине по меньшей величине по величине к обычному LSF. В принципе, это приводит к улучшению собственных векторных композиций и, следовательно, к улучшению вероятностей перехода. В некоторых случаях уточнения целесообразны, и они будут обсуждаться ниже. В таблице 1 некоторые характеристики обоих методов установлены рядом.
Термин анализ комплексных спектров, таких как Mn IV [7], Re III [1] и Os III [2], достиг только точности предсказаний ортогональных операторов. Такие прогнозы касаются как уровней энергии, так и интенсивности электрических диполей.
Кроме того, надежные расчеты запрещенных магнитных дипольных и электрических квадрупольных интенсивностей обеспечиваются точными эгальными энвекторами от ортогонального оператора LSF соответствующей системы. На более теоретическом уровне использование ортогональных операторов позволяет установить небольшие и до сих пор игнорируемые взаимодействия, отражающие многотелесные, релятивистские и корреляционные эффекты.
Подход ортогонального оператора кратко рассматривается и сравнивается с обычным LSF подход. Тем повышенный устойчивость из прямоугольных Операторов Создает комната Кому Содержательн включать двухэтажный магнитный Операторов и верхний порядок эффективный электростатический Операторов. Тем значить ЛСФ ошибка тем самым существенно сокращается, что должно давать лучшие собственные векторные композиции и улучшенные переход Вероятности. Однако 'ортогональный операторов есть конечно нет подключи и играй метод: начальный ESTИматесы требуют изоионной/изоэлектронной экстраполяции, предварительно ab initio расчеты или оба. Опыт работы с соседними спектрами, очевидно, помогает. Мало опыта было накоплено в открытый pn и f n оболочек пока нет, хотя недавно мы реализовали ортогональные операторы для обоих случаев; Приложений для f n Конфигурации с n 2 ар плановый в тем близкий будущее.
В то время как крупномасштабные вычисления с кодом Коуэна (включая множество индивидуальных конфигураций) определенно приводят быстрым и надежным способом к удовлетворительным результатам, важные магнитные эффекты остаются за столом, и это может представлять проблему для близких уровней. Ортогональные операторы (включая многие эффективные операторы) по своей природе более возмущены, чем вариационные. Что касается электростатических эффектов более высокого порядка, то нелегко сравнить воздействие большого числа ненаблюдаемых, масштабированных конфигураций (которые действительно выступают в качестве эффективных операторов) с эффективными ортогональными операторами 3- и 4-тел: они, вероятно, представляют одни и те же эффекты только частично. Когда в игру вступает сильное конфигурационное взаимодействие, ортогональное пространство модели расширяется ограниченным числом конфигураций. Средняя погрешность LSF все еще явно меньше, но ближе к среднему error обычного подхода в этих случаях.
В данной статье мы рассмотрели более точечный пример, как ортогональные операторы помогают решить важнейшие задачи в других научных областях, а именно в физике.

