Компьютерное моделирование критического поведения слабо неупорядоченной модели Поттса с тремя спиновыми состояниями методом коротковременной динамики

STADY OF CRITICAL BEHAVIOR OF A WEAKLY DISORDERED POTTS MODEL WITH THREE SPIN COMPONENTS BY THE METHOD OF SHORT-TIME DYNAMICS

Vasily Borodikhin

candidate of Science, associate Professor, Omsk state University, Russia, Omsk

Аннотация. Методом коротковременной динамики исследовано поведение слабо неупорядоченной трехмерной модели Поттса с числом спиновых компонент равным трем, со спиновой концентраций 0.95. Вычислены динамический индекс z, и критический индекс ν с учетом поправок к скейлингу.

Abstract. The behavior of a weakly disordered three-dimensional Potts model with the number of spin components equal to three, with a spin concentration of 0.95, was investigated by the method of short-time dynamics. The dynamic index z and the critical index ν are calculated taking into account corrections to scaling.

Ключевые слова: модель Поттса; динамический критический индекс.

Keywords: Potts model; dynamic critical index.

Введение

Проблема фазовых переходов в неупорядоченных системах представляет большой теоретический и экспериментальный интерес. Это связано с тем, что большинство реальных твердых тел содержит примеси и другие дефекты структуры, присутствие которых влияет на их термодинамические характеристики и, в частности, может существенно влиять на поведение систем при фазовых переходах. В частности представляет интерес исследование критического поведения слабо неупорядоченной модели Поттса с числом спиновых состояний q=3, с использованием методов не применявшихся ранее для исследования данной модели, в частности  методом коротковременной динамики.

Трехмерная модель Поттса с примесями и моделирование

Модель Поттса с числом спиновых состояний q=3 находит широкое применение при описании ряда объектов и явлений в физике конденсированных сред таких как сложные анизотропные ферромагнетики кубической структуры, многокомпонентные сплавы и жидкие смеси.

Структурные фазовые переходы в некоторых материалах, таких, как SrTiO3 или Pb3(PO4)2 относятся к классу универсальности трехкомпонентной модели Поттса.

Данная модель имеет следующие основные особенности. В узлах кубической решётки расположены спины, которые могут находиться в одном из 3-x спиновых состояний, и немагнитные примеси. Немагнитные атомы примеси распределены случайным образом и являются фиксироваными в узлах решетки. Энергия связи между двумя узлами равна нулю, в случае если они находятся в разных состояниях, или если в одном узлов находится немагнитная примесь, и равна J, если взаимодействующие узлы находятся в одинаковых состояниях, где J - обменный интеграл.

Гамильтониан модели имеет вид:

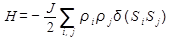,                                                                                                        (1)

где Si, q=1, 2, 3, δ(Si,Sj)=1 при  Si   = Sj и  δ(Si,Sj)=0 при Si   ≠ Sj ;  ρi  = 1, если в узле находится спин, и  ρi  = 0,  если в узле находится немагнитая примесь.

 Для моделирования системы в работе применялся алгоритм Метрополиса. В качестве намагниченности m для разбавленной модели Поттса использовалось следующее выражение [1]:

                                                                                                            (2)

где Nmax=max {N1 , N2 , N3} , N1 - число спинов в состоянии с q = 1, N2 - число спинов в состоянии с q = 2, N3 - число спинов в состоянии с q = 3,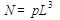.При исследовании динамических свойств модели Поттса применялся метод коротковременной динамики [2].  

Результаты моделирования

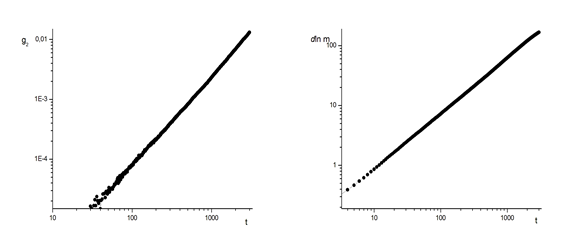
 (а)                                                       (б)

Рисунок. 1. Временная зависимость (а) кумулянта 2-го порядка (б) логарифмической производной

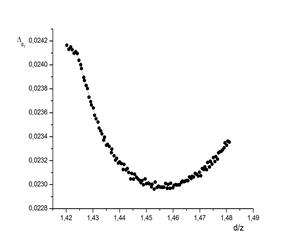
(а)                                                    (б)

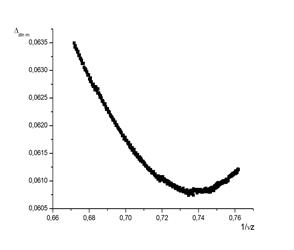
Рисунок. 2. Минимум погрешности (а) показателя d/z (б) показателя логарифмической производной

Исследовалась спиновая конфигурация p=0,95. Линейный размер системы брался равным L=128. Производилось вычисление динамической зависимости кумулянта второго порядка, и логарифмической производной, ΔT=0,002.  Статистическое усреднение осуществлялось по 6800 примесным конфигурациям. Результаты моделирования приведены на рис. 1.а-б. С учетом поправок к скейлингу найдены значения показателей d/z=1,452±0,0011  (ω/z=0,392±0,004), 1/νz=0,73457±0,0008  (ω/z=0,40±0,0045), соответствующие минимумы погрешностей показаны на рис. 2.а-б.  Из полученных значений показателей, соответственно, значение динамического критического индекса z=2,0657±0,0022, и значение критического индекса ν=0,6590±0,003.

Заключение

Исследование модели Поттса с q=3 в статическом случае [2], при малых концентрации примесей показало, что внесение примесей приводит к новому типу критического поведения, при этом в системе реализуется фазовый переход второго рода. Проведенные, методом коротковременной динамики исследования  подтвердили данные результаты, уже для малой концентрации примесей p=0,95 фазовый переход 1-го рода меняется на фазовый переход 2-го рода. Значение динамического критического показателя z, для модели Поттса с учетом поправок к скейлингу имеет немного меньшее значение по сравнению с индексом z, найденным для модели Изинга при той же концентрации примесей [3]. Возможно это связано с влиянием дополнительной спиновой компоненты. Значение индекса ν близко к значению, найденному в [2] для модели Поттса с концентрацией примесей p=0,95 статическими методами.

Список литературы:
1.    Муртазаев А.К., Бабаев А.Б., Азнаурова Г.Я., Особенности фазовых переходов в трехмерных разбавленных структурах, описываемых моделью Поттса // ЖЭТФ. 2009. Т.136. С. 520.
2.    Zheng B. Monte Carlo simulations of short-time critical dynamics // Comp. Phys. Comm. 1999. V. 121. P. 338.
3.    Prudnikov P.V.,  Prudnikov V.V.,  Krinitsyn A.S.,  Vakilov A.N.,  Pospelov E.A., Short-time dynamics and critical behavior of three-dimensional site-diluted Ising model // Phys. Rev. E. 2010. V. 81. P. 011130.