Анализ процессов повторного возбуждения сварочной дуги
Конференция: XVI Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Секция: Электротехника

XVI Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Анализ процессов повторного возбуждения сварочной дуги
Ekaterina Kerzhentseva
student Samara State Technical University SSTU, Russia, Samara
Аннотация. Процессы, протекающие в стволе сварочной дуги, при повторном возбуждении достаточно сложны и определяют условие ее устойчивого горения. Периодическое изменение величины напряжения источника переменного тока, а, следовательно, и сварочного тока, питающего дугу, вызывает периодическое погасание и зажигание дуги, т. е. приводит к «перерывам» в горении дуги.
Abstract. The processes occurring in the barrel, when re-excited are quite complex and determine the condition of its stable combustion. The periodic change in the voltage of the alternating current source, and, consequently, the welding current that feeds the arc, causes periodic extinction and ignition of the arc, i.e. leads to "breaks" in the arc combustion.
Ключевые слова: сварочная дуга; коммутационные аппараты; источник питания; вихревые токи; сварочный трансформатор
Keywords: welding arc, switching devices, power supply, eddy currents, welding transformer
Можно отметить два механизма возбуждения сварочной дуги: возбуждение остаточной плазмой и возбуждение током электронной эмиссии [1, 2, 4]. Но процесс возбуждения ствола дуги нельзя рассматривать отдельно от динамических свойств источника питания.
Сравнение динамических свойств коммутационных аппаратов и в том числе сварочных трансформаторов в основном проводится по методике, изложенной в литературе [1, 2].
При работе сварочного трансформатора в его феромагнитных элементах возникают вихревые токи, оказывающие существенное влияние на процесс восстановления напряжения. В схеме замещения сварочного трансформатора контуры вихревых токов в первом приближении могут быть заменены одним эквивалентным, имеющим магнитную связь с цепью сварочного тока. На рис. 1 представлена упрощенная схема замещения однофазного сварочного трансформатора. Здесь L1 и r1 - соответственно индуктивность и активное сопротивление источника: rВ и LВ - активное сопротивление и индуктивность эквивалентного контура вихревых токов, r1 и r1+rэ - сопротивление межэлектродного промежутка до и после погасания дуги. Переходный процесс, возникающий при повторном возбуждении дуги, моделируется размыканием ключа K, т. е. полагается скачкообразное изменение сопротивления столба дуги от значения r1 до r1+rэ (инерционностью процессов в столбе дуги пренебрегаем:  ).
).
Пусть напряжение источника изменяется по закону синуса:

Тогда на основании второго закона Кирхгофа после коммутации имеем (рис. 1):

Рисунок 1. Схема замещения сварочного трансформатора в переходном режиме
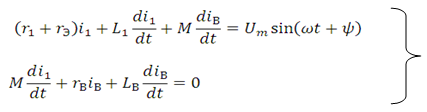 (1)
(1)
Рассмотрим, как будет изменяться напряжение на электродах при условии, что дуга гаснет в момент перехода сварочного тока через нулевое значение, т. е. i1=0, но iВ≠0.
Используя преобразование Лапласа [3], система уравнений (1) в операторной форме примет вид:
 (2)
(2)
Решая систему (2) относительно функции I1(P), получим
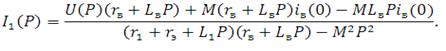 (3)
(3)
Знаменатель выражения (2) может быть представлен в виде:

Вводя обозначения

где: К – коэффициент связи контуров;  – коэффициент рассеяния;
– коэффициент рассеяния;
 – соответственно коэффициенты затухания контуров.
– соответственно коэффициенты затухания контуров.
Получим характеристическое уравнение:

Здесь «b», очевидно, вещественное число, причем
 , и
, и  .
.
В большинстве практических случаев

где: 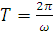 - период синусной функции источника питания.
- период синусной функции источника питания.
Учитывая это, можно сказать, что
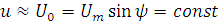 .
.
Выражение для изображения функции I1(P), может быть записано в виде
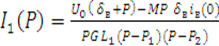
Рассмотрим два предельных случая.
Первый случай: К=1
Используя правило Лопиталя получим выражения для корней характеристического уравнения:

Получим:

Второй случай: К=0, т. е. между контурами нет магнитной связи. Тогда схема замещения трансформатора может быть представлена одним контуром, и решение в этом случае примет вид [3]:

Учитывая, что в процессе повторного зажигания принужденная составляющая напряжения изменяется по закону синуса, а характер свободной составляющей полностью совпадает с рассмотренным случаем, полученный результат можно распространить и на питание дуги от источника переменного тока. Нижний предел возвращающейся составляющей восстанавливающегося напряжения определяет напряжение зажигания дуги. Если окажется, что оно меньше напряжения зажигания, то при любой скорости восстановления напряжения дуга не загорится (рис. 2).
Из выражения (4) следует, что на характер процесса восстановления напряжения существенное влияние оказывает коэффициент связи «К». Так, например, при К=0 P1=P2 и процесс восстановления практически определяется одной экспонентой (рис. 2). По мере увеличения величины К постоянная времени цепи τ1 растет, а постоянная величина времени ствола дуги τ2 падает, что приводит к увеличению скорости восстановления загорания дуги. Сказанное выше хорошо согласуется с полученными опытными данными и подтверждается рядом ранее опубликованных работ [1, 2, 4].
Таким образом, если динамические свойства ствола электрической дуги можно учесть соответствующей моделью (С.И. Тельского, Г.И. Лескова, Майра и Кесси) [1], то динамические свойства источника питания лучше определить индикаторным методом, основанном на применении теоремы Тевинина.

