Новое о степени сжатия в поршневых двигателях с подводом теплоты при постоянном объёме
Конференция: XLVI Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Секция: Транспорт

XLVI Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Новое о степени сжатия в поршневых двигателях с подводом теплоты при постоянном объёме
NEW ABOUT THE COMPRESSION RATIO IN PISTON ENGINES WITH HEAT INPUT AT A CONSTANT VOLUME
Nodir Kodirov
Independent research, Uzbekistan
Аннотация. Вниманию научного сообщества предлагается переосмысленное понимание степени сжатия поршневых двигателей с подводом теплоты при постоянном объёме.
Abstract. The attention of the scientific community is offered a rethought understanding of the compression ratio of piston engines with heat input at a constant volume.
Ключевые слова: поршневой двигатель; подвод теплоты при постоянном объёме; степень сжатия.
Keywords: piston engine; heat input at a constant volume; compression ratio.
Из технической термодинамики известно, что термический КПД идеального цикла Отто, состоящего из двух адиабат и двух изохор, равен [1, с.21]:
![]() (1)
(1)
где ε-степень сжатия, ![]() , где Va- полный объём цилиндра,
, где Va- полный объём цилиндра, ![]() , где Vh- рабочий объём цилиндра,
, где Vh- рабочий объём цилиндра, ![]() , где D-диаметр цилиндра, S-ход поршня, Vhc- объём камеры сгорания,
, где D-диаметр цилиндра, S-ход поршня, Vhc- объём камеры сгорания, ![]() , где hc-высота камеры сгорания [3, с. 62], k-показатель адиабаты.
, где hc-высота камеры сгорания [3, с. 62], k-показатель адиабаты.
«Обратимый адиабатный процесс можно осуществить в цилиндре с абсолютно нетеплопроводными стенками при бесконечном медленном перемещении поршня» [2, с. 85]. В идеальном цикле Отто расширение и сжатие рабочего тела совершаются по адиабате, в такте расширение, по определению, давление и температура рабочего тела снижаются, а в такте сжатие, напротив, давление и температура рабочего тела повышаются [2, с. 238]. В обоих этих тактах имеет место быть такое положение поршня, при котором текущее давление в цилиндре равно среднему давлению в такте, причем такой анализ выявил интересную неожиданность. В профильной научной литературе определение среднего давления в такте не рассматривается, однако его можно вывести на основании следующих уравнений:
![]() и
и ![]() [2, с. 240], где Lц- полезная работа цикла, Le-работа изменения объема в такте расширение, Lc- работа изменения объёма в такте сжатие, pi- среднее индикаторное давление. Преобразуем уравнение среднего индикаторного давления с учетом того, что
[2, с. 240], где Lц- полезная работа цикла, Le-работа изменения объема в такте расширение, Lc- работа изменения объёма в такте сжатие, pi- среднее индикаторное давление. Преобразуем уравнение среднего индикаторного давления с учетом того, что ![]() , откуда следует, что
, откуда следует, что ![]() :
:
![]() , где выражение
, где выражение ![]() есть среднее давление в такте расширение реср, т. е.
есть среднее давление в такте расширение реср, т. е. ![]() , а выражение
, а выражение ![]() есть среднее давление в такте сжатие рср, т.е.
есть среднее давление в такте сжатие рср, т.е. ![]() .
.
Такт расширение. Поршень движется от ВМТ к НМТ, давление снижается по закону:
![]() [2, с. 239], где pz- давление в начале такта, pb-давление в конце такта, ε-степень сжатия, k- показатель адиабаты, Λ- степень повышения давления,
[2, с. 239], где pz- давление в начале такта, pb-давление в конце такта, ε-степень сжатия, k- показатель адиабаты, Λ- степень повышения давления, ![]() [2, с. 236], pc- давление в конце такта сжатие.
[2, с. 236], pc- давление в конце такта сжатие.
При достижении поршнем некоторого положения, текущее давление в цилиндре становится равным среднему давлению в такте:
![]()
![]() ,
,
где εeср-степень сжатия при этом положении поршня.
Как показано выше, среднее давление в такте реср:
![]()
Работа изменения объема:
![]() [2, с. 86],
[2, с. 86],
т. к.
![]() ,
,
то:
![]() ,
,
а т. к. ![]() [2, с. 86],
[2, с. 86],
и ![]() ,
,
то:
![]()
Среднее давление в такте реср:
![]() ,
,
так как
![]() ,
,
то:
![]()
Приравниваем:
![]()
откуда:
![]() ,
,
и:
![]()
окончательно:
![]() (2)
(2)
Такт сжатие. Поршень движется от НМТ к ВМТ, давление повышается по закону:
![]() [2, с. 238], где pa- давление в начале такта, pc-давление в конце такта, ε-степень сжатия, k- показатель адиабаты.
[2, с. 238], где pa- давление в начале такта, pc-давление в конце такта, ε-степень сжатия, k- показатель адиабаты.
При достижении поршнем некоторого положения, текущее давление в цилиндре становится равным среднему давлению в такте:
![]()
![]() ,
,
где εcср-степень сжатия на этом угле ПКВ.
Среднее давление во всем такте рcр:
![]()
Работа изменения объема:
![]() [2, с. 86],
[2, с. 86],
![]() ,
,
а т. к.
![]() [2, с. 86]
[2, с. 86]
и
![]() ,
,
то:
![]()
Среднее давление в такте рсср:
![]() ,
,
так как
![]() ,
,
то:
![]()
Приравниваем:
![]()
![]()
откуда:
![]()
Так как:
![]() [2, с. 86],
[2, с. 86],
То:
![]() ,
,
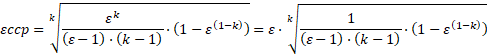
![]() (3)
(3)
Произведение степеней сжатия εеср и εcср:
![]() и
и ![]()
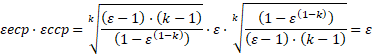
![]() (4)
(4)
Если посмотреть на примере [1, с.167], то степень сжатия εеср при заявленной степени сжатия ε=8 [1, с.168] и среднем показателе политропы расширения n2=1,23 [1, с.170] по уравнению (2):
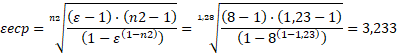
а степень сжатия εсср при среднем показателе политропы сжатия n1=1,37 [1, с.169] по уравнению (3):
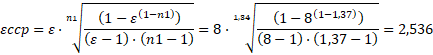
Тогда произведение степеней сжатия εеср и εсср вместо равенства заявленной степени сжатия ε=8 в примере [1, с.168] по уравнению (4) составит:
![]()
В том же самом можно убедиться на примере [3, с.171], где степень сжатия εеср при заявленной степени сжатия ε=8 [3, с.170] и среднем показателе политропы расширения n2=1,28 по уравнению (2):
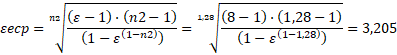
а степень сжатия εсср при среднем показателе политропы сжатия n1=1,34 по уравнению (3):
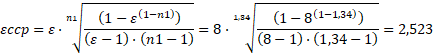
Тогда произведение степеней сжатия εеср и εсср вместо равенства заявленной степени сжатия ε=8 в примере [3, с.170] по уравнению (4) составит:
![]()
Объясняется это тем, что уравнение (4) справедливо только при n2=n1, что в не соответствует действительности, так как в реальных двигателях всегда n2<n1. Вероятно, будет небесполезно, если научное сообщество обратит внимание на раскрытую в данной статье особенность степени сжатия в поршневых двигателях.

