Разработка методики составления математических моделей законов коммутации транзисторных ключей мостовой схемы вентильного преобразователя

Development of a methodology for compiling mathematical models of the switching laws of transistor keys of a bridge converter

Grigory Ohotkin

doctor of Technical Sciences, assistant professor, Chuvash State University, Russia, Cheboksary

Gennady Belov

doctor of Technical Sciences, professor, Chuvash State University, Russia, Cheboksary

Stanislav Ugarin

Assistant, Chuvash State University, Russia, Cheboksary

Аннотация. В работе разработана методика составления математических моделей законов коммутации транзисторных ключей мостовой схемы вентильного преобразователя на основе теории автоматов. Математические модели составлены с использованием двух автоматных языков: таблицы переходов и выходов и графы переходов. Граф автомата позволяет наглядно представить все переходы автомата из одного внутреннего состояния в другое, поэтому удобен для анализа алгоритмов, а таблицы переходов и выходов – для синтеза системы управления вентильным преобразователем.

Abstract. In the work the technique of compilation of mathematical models of switching laws of transistor keys of the bridge circuit of the gate converter is developed on the basis of the theory of automata. Mathematical models are compiled using two automaton languages: transition and output tables and transition graphs. The graph of the automaton allows you to visually represent all the transitions of the machine from one internal state to another, so it is convenient for analyzing the algorithms, and the transition and output tables for the synthesis of the control system of the gate converter.

Ключевые слова: вентильный преобразователь; законы коммутации транзисторных ключей; мостовая схема; регулируемый электропривод; синтез динамических систем.

Keywords: valve converter; switching laws of transistor switches; bridge circuit; adjustable electric drive; synthesis of dynamic systems.

Благодаря высокому быстродействию и низким массогабаритным показателям автоматизированный электропривод находит широкое применение в робототехнике и станкостроении. Регулируемые электроприводы (РЭП) с высокими динамическими показателями строятся на полупроводниковых преобразователях электроэнергии, силовая схема которых выполнена на транзисторах, а схема управления – по системе подчиненного регулирования координат с внутренним контуром тока и внешним контуром скорости. Дискретность и нелинейность силовой схемы полупроводниковых преобразователей электроэнергии наиболее ярко проявляются в контуре тока, представляющего собой систему автоматического регулирования (САР) тока. Динамические показатели электропривода определяются динамическими свойствами САР тока, поэтому синтез САР тока на предельное быстродействие является актуальной задачей при проектировании высокодинамичных РЭП.

Разработаны различные структуры системы управления САР тока. На практике наибольшее распространение получили структуры с управлением по отклонению, с управлением по отклонению и с положительной связью по падению напряжения на элементах нагрузки и комбинированные системы управления. Анализ точности вышеописанных структур выполнен в работе [1]. Регулирование напряжения на выходе полупроводниковых преобразователей электроэнергии осуществляется путем изменения длительности открытого состояния транзисторных ключей. При этом наибольшее распространение получили методы регулирования с широтно-импульсной модуляцией (ШИМ), частотно-широтно-импульсной модуляцией (ЧШИМ) и релейное регулирование.

Благодаря простоте и надежности релейные способы регулирования получили широкое распространение. Структурная схема релейной САР тока с принципом управления по отклонению состоит из релейного регулятора тока (РРТ), логического устройства (ЛУ), силовой схемы полупроводникового преобразователя электроэнергии, якорной или статорной цепи электродвигателя и датчика тока (ДТ).

При построении высококачественного реверсивного электропривода постоянного тока получила широкое распространение силовая схема полупроводникового преобразователя электроэнергии, выполненная на четырех транзисторах VT1 - VT4 с обратными диодами VD1 - VD4 по так называемой мостовой схеме, изображенная на рис. 1. Схему, выполненную на четырех транзисторах с обратными диодами, обозначим как вентильный преобразователь (ВП).

Рисунок 1. Мостовая схема вентильного преобразователя

Известно множество различных законов коммутации транзисторных ключей мостовой схемы вентильного преобразователя [2]. В работе [3] установлены наиболее эффективные законы коммутации ключей, применяемые на практике.

Проектирование быстродействующих систем силовой электроники является сложной задачей, состоящей из нескольких этапов. Одним из начальных и важных является этап разработки математических моделей законов коммутации ключей ВП. Математическая модель законов коммутации ключей ВП позволяет на последующих этапах осуществить структурный синтез релейного регулятора тока и логического устройства, формирующего импульсы управления транзисторами моста. Разработка математических моделей законов коммутации ключей ВП в доступной литературе освещены недостаточно полно, поэтому данная задача является актуальной.

Целью данной работы является разработка методики составления математических моделей законов коммутации ключей ВП, удобной для проектирования оптимальной системы управления вентильным преобразователем.

Коммутация транзисторных ключей ВП происходит дискретно. Поэтому алгоритм коммутации ключей ВП может быть представлен как конечный автомат. Особенностью такого представления является то, что при этом в явном виде удается описать входные, внутренние и выходные состояния, а также изменения этих состояний в процессе функционирования автомата. Для этого существуют различные языки описания автоматов. Наиболее удобными языками являются стандартные автоматные языки, позволяющие в явном виде задать функции переходов и выходов. В связи с этим для математического описания законов коммутации ключей ВП будем использовать два автоматных языка: таблицы переходов и выходов, графы переходов.

Чтобы задать автомат необходимо описать его внутренние состояния, состояния входов и выходов, а также функции переходов и выходов. Введя векторы входа , состояния автомата  и выхода , и представив через эти векторы функцию переходов  и функцию выходов  можно математическую модель автомата представить отображениями:

 в ,    на .                                                                               (1)

Абстрактный автомат (1) представляет собой шестикомпонентный кортеж, или вектор, . Компоненты векторов  конечны и поэтому автомат называется конечным. Автомат является полностью определенным, т.к. области определения функций  и h совпадают с множествами всевозможных пар вида .

Удобной формой представления математической модели закона коммутации ключей ВП является граф-схема автомата, состоящая из вершин и дуг. В кружках, соответствующих вершинам графа, отмечаются состояния автомата, а на стрелках, соответствующих дугам графа, отображают направления переходов. Около дуг в скобках отображают состояния входа, при которых происходит переход по соответствующей дуге, и через запятую указывают состояние выхода автомата. В результате этого граф-схема автомата более наглядна, чем таблица переходов и выходов, представляет переход автомата из одного внутреннего состояния в другое.

Подробнее рассмотрим приведенную выше методику для составления математической модели симметричного закона коммутации ключей мостовой схемы ВП. При симметричном законе в состоянии переключения находятся все четыре транзисторных ключа моста, а напряжение на выходе преобразователя представляет собой знакопеременные импульсы, длительность которых регулируется входным сигналом. Для этого знакопеременные управляющие импульсы подаются на все транзисторы моста: сначала отпирающие импульсы подаются на транзисторы VT1 и VT4, запирающие – на транзисторы VT2 и VT3, а затем наоборот.

Схема моста может работать в двух токовых режимах: в режиме непрерывного тока и в режиме переменного тока. В режиме непрерывного тока, когда включены транзисторы VT1 и VT4 моста, на выходе ВП формируется положительное напряжение . При этом в нагрузке протекает возрастающий по экспоненциальному закону ток. Состояние ВП, когда включены транзисторы VT1 и VT4, обозначим как Р2В режим два «Вперед».

На интервалах времени, когда отпирающие импульсы подаются на транзисторы VT2 и VT3, из-за открытых обратных диодов VD2 и VD3 транзисторы VT2 и VT3 не открываются. При этом в нагрузке протекает спадающий по экспоненциальному закону ток под воздействием напряжения . Состояние схемы, когда открыты обратные диоды VD2 и VD3, обозначим как Р0ДВ режим ноль с открытыми обратными диодами для направления вращения «Вперед». Так, переключая ключи с высокой частотой, в нагрузке формируется пульсирующий ток, среднее значение которого больше нуля I_я > 0.

В режиме переменного тока, когда ток нагрузки спадает до нуля и диоды VD2 и VD3 закрываются, транзисторы VT2 и VT3 открываются. При этом в нагрузке начинает возрастать по экспоненциальному закону ток отрицательной полярности под воздействием напряжения . Состояние моста, когда открыты транзисторы VT2 и VT3, обозначим как Р2Н режим два «Назад».

При закрытии транзисторов VT2 и VT3 открываются диоды VD1 и VD4 и ток нагрузки начинает спадать под воздействием напряжения . Такое состояние схемы обозначим как Р0ДН режим ноль с открытыми диодами для направления вращения «Назад».

Исходя из вышесказанного, закодируем внутренние состояния автомата как x_n={Р0, Р2В, Р0ДВ, Р2Н, Р0ДН}  , а вектор состояния автомата – .

Состояния транзисторов схемы моста (открыт – закрыт) определяются управляющими импульсами: U_БЭ1… U_БЭ4. Для удобства описания автомата принимаем, что при U_БЭi = 0 i-й транзистор моста закрыт, а при U_БЭi = 1 – открыт. Учитывая все возможные комбинации управляющих импульсов U_БЭi закодируем их состояния через и представим результаты кодирования в табл.1.

Таблица 1.

Кодирование состояний входов

Следовательно, вектор входа автомата представляется как .

Выходное напряжение моста при работе схемы ВП может принимать три значения: 0; U_п; -U_п. Поэтому закодируем состояния выхода автомата как u_j={0, U_п, -U_п } , а вектор выхода – .

Так, на основе анализа работы схемы моста ВП и отображений (1) составлены таблица переходов (табл. 2) и таблица выходов (табл. 3). Строкам таблицы переходов соответствуют состояния входов, а столбцам – состояния ВП, причем крайний левый столбец обозначен начальным состоянием x₁. На пересечении столбца x_m и строки  в таблице переходов ставится состояние , в которое автомат переходит из состояния x_m под воздействием сигнала .

Таблица 2.

Таблица переходов

В таблице выходов (табл. 3) на пересечении столбца x_m и строки  ставится состояние выхода , соответствующее переходу автомата.

Таблица 3.

Таблица выходов

Полученные таблицы переходов и выходов описывают абстрактный автомат, являющийся математической моделью симметричного закона коммутации ключей ВП.

Граф-схема автомата представлена на рис. 2, которая позволяет наглядно представить все переходы автомата из одного внутреннего состояния в другое [4].

Рисунок 2. Граф-схема симметричного закона коммутации ключей ВП

Далее разработаем математическую модель диагонального закона коммутации ключей с переключением верхнего транзистора мостовой схемы вентильного преобразователя [5].

При диагональной коммутации осуществляется раздельное управление комплектами вентильных преобразователей, состоящих из диагональных транзисторов моста VT1 и VT4 или VT2 и VT3. Причем в работающем комплекте ВП переключаются верхние транзисторы VT1 (VT2) при постоянно открытых нижних транзисторах VT4 (VT4). В результате этого в нагрузке моста протекает ток, содержащий минимальные пульсации.

В отличие от предыдущего закона коммутации ключей здесь дополнительно возникают режимы: Р1В – режим один «Вперед», когда включен один нижний транзистор VT4 моста; Р1Н – режим один «Назад», когда включен только один нижний транзистор VT3; Р0В – режим ноль «Вперед», все транзисторы выключены, ток нагрузки равен нулю, а противо-ЭДС E_я > 0, т.е. электродвигатель вращается «Вперед»; Р0Н – режим ноль «Назад», транзисторы выключены, ток нагрузки равен нулю, а E_я < 0. Режимы Р0В и Р0Н системы «ВП-ДПТ» являются неустойчивыми и с остановом электродвигателя, переходят в режим Р0.

На основе анализа электромагнитных процессов в системе устанавливаем, что состояние мостовой схемы ВП (без учета состояния ДПТ) характеризуется следующими семью режимами: Х={Р0, Р2В, Р1В, Р0ДВ, Р2Н, Р1Н, Р0ДН}. При непрерывных токах нагрузки пять режимов Р0, Р2В, Р1В, Р2Н и Р1Н являются устойчивыми и два режима Р0ДВ и Р0ДН – неустойчивыми, а в режиме прерывистого тока нагрузки устойчивыми являются три режима Р0, Р2В и Р2Н, и неустойчивыми – следующие четыре режима Р1В, Р0ДВ, Р1Н и Р0ДН.

С учетом состояния ДПТ закодируем состояния выходного напряжения ВП как  , где  - означает, либо u_я = 0, либо . Учитывая все возможные комбинации управляющих импульсов U_БЭi транзисторов моста ВП. Также закодируем состояния управляющих импульсов транзисторами через  и представим результаты кодирования в табл. 4.

Таблица 4.

Кодирование входных воздействий

Граф-схема алгоритма диагонального закона коммутации ключей с переключением верхнего транзистора мостовой схемы вентильного преобразователя приведена на рис. 3.

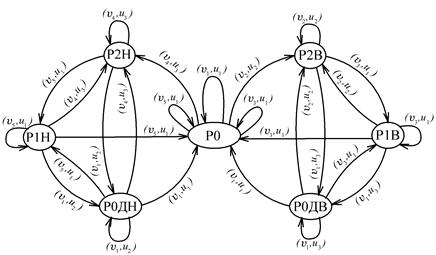
Рисунок 3. Граф-схема диагонального закона коммутации ключей с переключением верхнего транзистора моста

Теперь без подробных пояснений приведем граф-схемы алгоритмов классического несимметричного и поочередного несимметричного законов коммутации ключей мостовой схемы вентильного преобразователя, разработанные в работах [6, 7].

При несимметричной коммутации в противофазе переключаются транзисторные ключи, расположенные в одной из стоек мостовой схемы (VT1,VT3 или VT2,VT4). При этом один из двух ключей VT3 или VT4 замкнут, а другой VT1 или VT2 разомкнут. Здесь имеется возможность переключать ключи, расположенные в одной стойке мостовой схемы при постоянно открытом транзисторе другой стойки.

Схема может работать в двух токовых режимах: в режиме непрерывного тока (РНТ) и в режиме знакопеременного тока (РЗПТ). В режиме непрерывного тока временные диаграммы работы ВП совпадают с временными диаграммами диагонального закона коммутации ключей с переключением верхнего транзистора моста. В режиме знакопеременного тока после закрытия транзистора VT1 открывается транзистор VT3. Когда ток нагрузки положительной полярности спадает до нуля, закрывается транзистор VT4 и под действием противо-ЭДС двигателя ток якоря отрицательной полярности потечет через открытый транзистор VT3 и диод VD4. При этом отрицательный ток в нагрузке начинает возрастать по экспоненциальному закону. Циклическое переключение транзисторов VT1 и VT3 формирует в нагрузке знакопеременный ток.

Граф-схема алгоритма классического несимметричного закона коммутации ключей мостовой схемы вентильного преобразователя представлена на рис. 4.

Рисунок 4. Граф-схема алгоритма классического несимметричного закона коммутации ключей ВП

На рис. 5 представлена граф-схема алгоритма поочередного несимметричного закона коммутации ключей мостовой схемы вентильного преобразователя.

Поочередная несимметричная коммутация ключей ВП основана на классическом несимметричном законе коммутации, алгоритм которого заключается в переключении в противофазе транзисторных ключей, расположенных в одной стоке, при постоянно открытом транзисторе другой стойки. Схема отличается от предыдущей наличием режимов Р1В – режим один «Вперед», когда открыты транзистор VT4 и диод VD3 и Р1В’ – режим один «Вперед» штрих, когда открыты транзистор VT1 и диод VD2. При этом частота коммутации транзисторов моста в два раза меньше частоты пульсаций тока нагрузки и осуществляется равномерная загрузки вентилей мостовой схемы ВП.

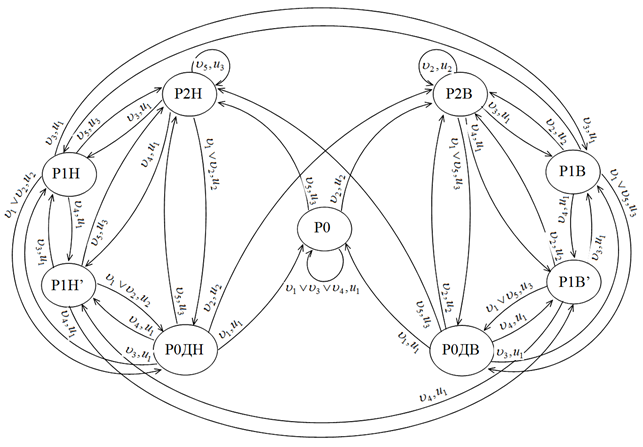
Рисунок 5. Граф-схема алгоритма поочередного несимметричного закона коммутации ключей ВП

Таким образом, используя два автоматных языка таблицы переходов и выходов и графы переходов разработана методика составления математических моделей алгоритмов коммутации ключей ВП. Полученные математические модели будут использованы в дальнейшем при синтезе системы управления мостовой схемы вентильного преобразователя.