Динамический расчет вибрационного механизма узла приема готовой газетной продукции офсетной рулонной машины

Аннотация. В статье представлена методика и выполнение практического расчета приведения внешней силы трения при гармонических колебаниях массы к эквивалентной диссипативной силе, что позволяет составлять и решать уравнение гармонических колебаний с учетом не только упруго-диссипативных сил, но и реальных сил трения.

Ключевые слова: рулонная машина; газетная продукция.

Одним из важнейших узлов современной полиграфической офсетной рулонной машины является узел приёма и транспортирования готовой газетной продукции. От рациональной конструкции этого узла и эффективности его работы в значительной степени зависит производительность и надёжность печатной машины в целом.

Существующие узлы выдачи и транспортировки готовой продукции современных газетных машин обладают серьёзным производственным недостатком, а именно: в общем потоке готовой газетной продукции отдельные экземпляры выбиваются в стороны из общего ряда. Это приводит к смятию и разрыву отдельных газетных экземпляров, их застреванию на линии транспортирования и нарушению порядка движения всего потока, что требует аварийной остановки машины и влечёт за собой угрозу срыва всего печатного тиража. Поэтому вопрос надежного и эффективного выравнивания и упорядочения движения газетной полосы является важным и актуальным.

В Уральском федеральном университете разработана конструкция вибрационного механизма дебалансного типа, создающего инерционную центробежную силу, циклически меняющуюся по направлению и вызывающую возвратно-поступательное движение массы механизма. Частота и амплитуда возвратно-поступательного движения определяются конструкцией и параметрами механизма и могут изменяться в широком диапазоне.  Суммарная движущая сила определяется моментом инерции дебалансов и частотой их вращения.

Величина суммарной движущей силы, создаваемой двумя дебалансами:

где:  – масса дебаланса;

 – радиус инерции дебаланса;

 – угловая скорость вращения дебаланса.

Знакопеременная циклически изменяющаяся движущая сила Ф вызывает высокочастотное возвратно-поступательное движение механизма, позволяющее целенаправленно формировать газетную стопу.

Для формирования рационального закона движения механизма, определения его амплитудно-частотных и инерционных параметров необходимо  решение дифференциального уравнения колебательного движения массы механизма. В уравнении должны быть учтены упругие и диссипативные силы, а также реально существующие  силы трения.

Классическое дифференциальное уравнение линейного движения массы при гармонических колебаниях имеет вид:

,

где М – масса движущихся частей механизма,

F – сила упругой деформации пружин, используемых в механизме,

,

R –  сила вязкого трения, пропорциональная первой степени скорости

,

где – коэффициент рассеяния энергии,

Ф – периодическая возмущающая сила.

После подстановки выражений упругих, диссипативных и возмущающих сил получаем:

Дифференциальное уравнение гармонических колебаний в таком классическом виде не учитывает реальных сил трения, имеющих величину, сопоставимую и даже превосходящую диссипативные силы. Значительные по величине силы трения существенно изменяют закон колебательного движения массы механизма. Это диктует необходимость введения реальной силы трения в уравнение колебаний. Однако введение этой силы в явном виде в уравнение гармонических колебаний, т. е. введение дополнительного члена уравнения, делает это уравнение аналитически нерешаемым.

Для сохранения уравнения колебаний в решаемом виде введем в это уравнение силу внешнего трения в виде эквивалентной ей диссипативной силы, т. е. выполним приведение силы внешнего трения к эквивалентной диссипативной силе. Приведение состоит в преобразовании постоянной по величине силы трения к эквивалентной, но переменной по величине диссипативной силе, зависящей от линейной скорости колебаний. Условием эквивалентного преобразования является равенство за цикл работы сил трения и работы эквивалентной диссипативной силы.

Мгновенная эквивалентная диссипативная сила RЭ определится равенством:

где:  – неизвестный (искомый) коэффициент диссипации,

 – мгновенная скорость движения колеблющейся массы

где: В – амплитуда колебаний,

 – частота возмущающей силы, создаваемой дебалансами.

После подстановки получаем:

Элементарная работа dA переменной диссипативной силы

dS – элементарное перемещение

Полная работа эквивалентной диссипативной силы на перемещении массы вибрационного механизма из одного крайнего положения в другое, т. е. на перемещении S=100 м, определится интегралом:

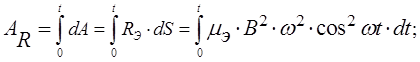
где:  t – время поворота дебалансов при перемещении механизма на S=100 м при  .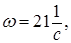

Определяем работу эквивалентной диссипативной силы.

Работа сил трения:

По условию равенства за цикл работ силы трения и эквивалентной диссипативной силы получаем:

Определяем эквивалентный коэффициент диссипации

Найденное значение эквивалентного коэффициента диссипации позволяет ввести постоянную по величине реальную силу трения в уравнение гармонических колебаний массы вибрационного механизма в виде переменной по величине эквивалентной диссипативной силы. Это позволяет составлять и решать уравнение гармонических колебаний с учетом не только упруго-диссипативных сил, но и реальных сил трения.

Список литературы:

1.  Артоболевский И.И. Теория механизмов и машин: Учебник для втузов. –4-е изд., перераб. и доп. – М.: Наука. Гл. ред. физ.-мат. лит., 1989. – 640 с.

2.     Левитская О.Н., Левитский Н.И. Курс теории механизмов и машин: Учебник для вузов. – М.: Высш. школа, 1978. – 269 с.

3.     Никитин Е.Н. Теоретическая механика. – М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 336 с.