Компьютерное конструирование полимерных композиций
Конференция: X Международная научно-практическая конференция "Научный форум: технические и физико-математические науки"
Секция: Информатика, вычислительная техника и управление

X Международная научно-практическая конференция "Научный форум: технические и физико-математические науки"
Компьютерное конструирование полимерных композиций
Аннотация. В статье рассмотрена возможность компьютерного конструирования полимерных композиций путем решения задачи механики сплошной среды. Показана связь между свойством полимерных композиции и соответствующим им линиям уровней.
Ключевые слова: полимерные композиции; линии уровней; управляющие параметры.
Модификация свойств полимерных материалов является актуальной проблемой, и решение ее проводится различными способами. Наиболее распространенным и простым способом является так называемая структурная модификации, когда в полимерную матрицу вводятся армирующие добавки, не меняющие химическую природу полимера. Хотя армирование традиционно связывается в основном с изменением прочности, спектр свойств, которые можно менять таким путем, очень широк, и включает в себя, в частности, такие группы характеристик материалов, как деформационно-прочностные, теплофизические и электрофизические [1].
Изменение деформационно-прочностных свойств обычно делается введением волокон, реже компактных частиц. В последнем случае изменение возможно, как в сторону упрочнения, когда вводимые частицы прочнее материала матрицы, так и в сторону повышения деформативности, когда требуется получить, например, ударопрочные или морозостойкие композиты за счет введения армирующих добавок с более низкими прочностными свойствами.
Сложность одновременного изменения свойств из разных групп в нужных направлениях связана с тем, что в большинстве случаев направленное изменение одних свойств ведет к изменению других, причем не всегда в нужном направлении. Достаточно привести характерный пример в этом отношении: улучшить теплопроводность материала можно, вводя в качестве армирующих добавок порошки металлов с высокой теплопроводностью. Эксперименты показывают, что деформационно-прочностные характеристики при этом заметно ухудшаются.
Из обзора публикаций в научно-технической литературе следует, что основным способом получением новых композиций является экспериментальный, базирующийся на информации о прототипах и аналогах. Способ требует больших материальных затрат, сложен в реализации, протяжен во времени, не гарантирует получения нужных свойств в заданных диапазонах.
Компьютерное моделирование наполненных композиций предполагает получение эффективных характеристик материалов по информации об управляющих параметрах – фазовом составе, внутренней геометрии, свойствах фаз, характере межфазного взаимодействия, технологических параметрах. Компьютерное конструирование решает обратную задачу – определение набора управляющих параметров, придающих заданные значения эффективным характеристикам. Очевидно, что компьютерное конструирование включает в себя моделирование как этап решения задачи. Использование компьютерного конструирования при разработке новых материалов позволяет оценить вклад различных управляющих параметров на свойства материала, понять физические процессы, происходящие в материале при этом. Рассмотрение возможности решения задачи механики сплошной среды для получения детальных характеристик полимерных коспозиций.
Для определения эффективных деформационно-прочностных свойств решается задача механики сплошной среды, когда проводится анализ напряженно-деформированного состояния (НДС) представительного объема неоднородного материала. Расчеты проводятся с использованием метода конечных элементов, реализующего вариационный принцип Лагранжа в форме метода перемещений. В расчетной области учитывается наличие односвязной области (полимерная матрица) и армирующих частиц. Расположение частиц в матрице определяется с помощью датчика случайных чисел, размеры частиц примерно одинаковы. На контакте реализуются различные условия – в одних случаях это идеальный контакт, предполагающий непрерывность перемещений и напряжений, в других реализован вариант с заданным уровнем адгезии, допускающий отрыв матрицы от включений. Результаты расчетов показывают известные эффекты, наблюдаемые в экспериментах – всплески напряжений вблизи контактных поверхностей, где скачком меняются свойства материалов, и локализация деформаций в матрице, более податливой по сравнению с армирующими частицами. Детальные распределения параметров НДС после применения процедур осреднения позволяют получить значения эффективных характеристик материала. Решением ряда задач при различных значениях управляющих параметров получается набор точек в пространствах состояний для каждой из эффективных характеристик, по которым можно построить соответствующие поверхности отклика. В работе это делается с использованием полиномов Лагранжа.
Расчет эффективных теплофизических свойств проводится в целом по такой же схеме: находятся детальные распределения температуры в задаче о распространении тепла по неоднородной среде, когда во внимание принимаются конкретные значения теплофизических свойств матрицы и армирующих частиц. В данном случае эти свойства являются одними из основных в числе управляющих параметров. За интегральные характеристики принимаются расстояние, на которое распространилось тепло от внешнего источника, или количество теплоты, накопленное в расчетной области. Для однородного тела сравнения получается, например, коэффициент теплопроводности из аналитического решения, когда используются полученные интегральные характеристики. Этот коэффициент принимается в качестве эффективной характеристики неоднородного материала. Далее в пространстве состояний по тому же правилу, что указано выше для деформационно-прочностных свойств, строится поверхности отклика коэффициента на значения управляющих параметров.
Электрофизическими характеристиками композиции являются диэлектрическая проницаемость и удельная электрическая проводимость. Задачи о параметрах электростатического поля решаются на основе уравнений Максвелла. После получений детальных распределений потенциала электрического поля осредненный, или эффективный, коэффициент диэлектрической проницаемости получается на основе сравнения энергии электростатического поля с энергией эквивалентного однородного материала. Энергия для неоднородного материала получается суммированием по отдельным ячейкам с учетом структуры материала и электрофизических свойств его структурных единиц (фаз).
Получение удельной электрической проводимости сводится к решению аналогичной задачи, отличающейся лишь матрицей физических коэффициентов конечного элемента – вместо произведений относительной диэлектрической проницаемости и электрической постоянной в первом случае используется проводимость во втором. В качестве критерия соответствия свойств однородного тела сравнения свойствам композита принимается равенство мощности тепловых потерь в проводниках.
Получение детальных распределений полей напряжений, деформаций и перемещений в первой группе задач, полей температуры во второй группе и потенциала электрического поля, напряженности поля в третьей группе делается на основе вариационных формулировок, реализуемых далее методом конечных элементов. Эффективные свойства материалов получаются с использованием условий равенства энергий деформаций в первом случае, теплоты во втором, энергии тепловых потерь в третьем.
На полученных поверхностях отклика эффективных свойств материала на значения управляющих параметров заданному значению свойства отвечает линия уровня в пространстве состояний. Если задаться диапазоном значений, получаем полосу. Когда число управляющих параметров равно двум – например, степень наполнения композита и средний размер армирующих включений, – в проекции этой полосы на плоскость управляющих параметров получаем их требуемый диапазон. Для другой характеристики получится другая полоса, а пересечение полос определит диапазон значений управляющих параметров, выводящих две характеристики в заданные интервалы.
|
|
|
|
Рисунок 1. Область значений управляющих параметров |
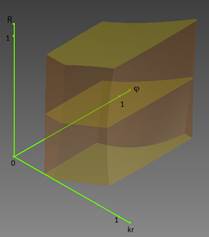
Рисунок 2. Область значений трех управляющих параметров (радиус включений R, степень наполнения φ, критерий отрыва включений от матрицы kr) |
На рис. 1 приведен пример построения искомой области управляющих параметров как пересечение пяти полос. Это означает, что в заданные диапазоны выводятся одновременно пять характеристик материала: 1) коэффициент теплопроводности (пунктирные линии); 2) диэлектрическая проницаемость (жирные линии); 3) удельная электрическая проводимость (штрихпунктирные линии); 4) предельная деформация разрушения (пунктирные линии с двумя точками); 5) предельное напряжение (пунктирные линии с тремя точками).
Сочетание управляющих параметров в полученной области дает решение задачи. В приведенном примере не все ограничения на требуемые свойства являются активными. В реализации на практике предпочтительны варианты, отвечающие точкам, наиболее удаленным от границ области, иначе при случайных возмущениях можно легко выйти за границу области.