Математическая модель процесса автоматического регулирования распределенных тепловых полей обитаемых подводных аппаратов на основе функции Грина

Mathematical model of the process of automatic regulation of distributed thermal fields of host underwater apparatuss based on the function of Greene

Senchilo Nikita

Saint-Petersburg Mining University, Russia, Saint-Petersburg

Аннотация. Статья описывает процесс автоматического регулирования распределенных тепловых полей обитаемых подводных аппаратов, для которых данный параметр является одним из важнейших для обеспечения оптимального функционирования всего аппарата. Использование функции Грина для математического описания процесса позволяет получить достаточно точное регулирования распределенных температурным полем с учётом всех значительных для процесса факторов.

Abstract. The article describes the process of automatic regulation of distributed thermal fields of inhabited underwater vehicles, for which this parameter is one of the most important for ensuring optimal functioning of the whole apparatus. The use of the Green function for the mathematical description of the process makes it possible to obtain a sufficiently accurate control of the temperature-field distributions taking into account all the factors that are significant for the process.

Ключевые слова: автоматическое регулирование; математическая модель; подводные аппараты; функция Грина; распределенные системы управления.

Keywords and phrases: automatic control; mathematical model; underwater vehicles; Green function; distributed control systems.

Для рассмотрения процесса стабилизации температуры необходимо рассмотреть замкнутую систему регулирования, представленную в виде следующей структурной схемы (рис.1):

Рисунок 1. Структурная схема замкнутой системы регулирования

Для указанной выше модели рассмотрена математическая модель на основе функции Грина.

Граничные условия u0(t), u1(t) для одномерного объекта, представляют собой воздействия, изменяющиеся во времени t. Так и пространственно-временные воздействия. Основное отношение, связывающее выход объекта при заданном начальном состоянии с входными воздействиями, может быть представлено в форме:

, где ξ и τ – переменные интегрирования по пространственной и временной координате [1].

Выход объекта Q(x,t) связывается с внешними воздействиями f, g0, g1 и начальным состоянием  соответствующими ядрами интегральных операторов , отражающими внутренние свойства объекта по отношению к соответствующим входам. Из общей теории линейных уравнений в частных производных следует, что все эти ядра могут быть выражены в конечном виде только через одну из них – функцию Грина .

Если

,

то в соответствии со свойствами дельта-функции получим:

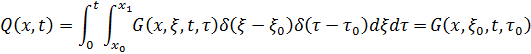
Таким образом, функция Грина является решением краевой задачи:

Импульсная переходная функция стационарного блока примет вид:

.

В достаточно общем случае соотношении между выходом и входом для нелинейного блока принимает вид следующего нелинейного интегрального оператора:

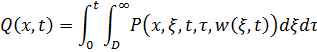
В полученное интегральное уравнение относительно функции состояния нелинейного объекта в форме:

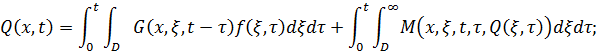
Расчет температурного поля объекта для автоматического регулирования производится с использованием следующего соотношения [3]:

Данное выражение определяет поведение объекта в начальный момент времени. Формула позволяет проанализировать поведение объекта при максимальной амплитуде импульса воздействия, так как объект в начальный момент времени находится в состоянии покоя.

Функция определяющая момент первого включения управляющего воздействия τ₁ в некоторый момент времени t будет определяться как одна из составляющих ряда Фурье:

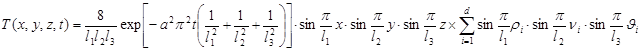
И, принимая , которое необходимо для обеспечения устойчивости системы, получим:

Полагая, что для данного уравнения присущи следующие равенства , ,  и обозначив время , получим:

;

откуда:

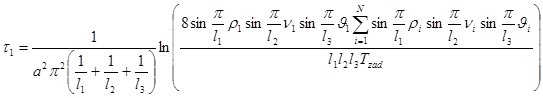
Аналогичным способом найдем место включения управляющего воздействия, которое согласно допускам указанным выше будет иметь вид:

Аналогично:

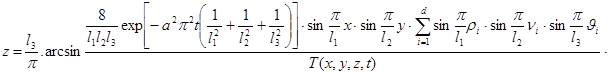
Для наглядного отображения результатов аналитического исследования был реализован блок управления температурным полем (рис.2) на печатной плате, который для упрощения анализа представлен с использованием средств программного пакета Multisim. Блок управления посылает управляющее воздействие на приборы регулирования температуры, которые обозначены на схеме R3 и R4, при определенных значениях температурного поля объекта:

Рисунок 2. Электронная схема САУ

Выводы о проведенном исследовании:

В статье реализована математическая модель системы автоматического регулирования распределенного температурного поля на основе функции Грина, которая математически описывает пространственно-временные взаимодействия параметров в процессе регулирования. Также реализован отдельный аспект системы управления в виде электронной схемы САУ на основе проведенного аналитического исследования.