Вероятностная оценка надежности нормальных сечений железобетонных ригелей

Probabilistic reliability assessment of reinforced concrete beam's standard profile

Nikolay Zhdanov

master of Unique Buildings and Constructions Department, Southwest State University, Russia, Kursk

Аннотация. Рассмотрен и описан метод оценки риска разрушения нормального сечения ригеля, армированного арматурой без предварительного натяжения с использованием метода статистических испытаний. Проведена количественная оценка риска разрушения нагруженных равномерно распределѐнной нагрузкой железобетонных ригелей.

Abstract. The article deals with a risk assessment method for standard profile fracture of non prestressed reinforced beam using Monte Carlo method. Also presented quantitative destruction risk assessment of reinforced concrete beams loaded with a uniformly distributed load.

Ключевые слова: вероятностная оценка; риск; нормальное сечение; предельное состояние.

Keywords: probabilistic assessment; risk; standard profile; limit state.

В настоящей работе рассмотрен метод оценки риска разрушения нормального сечения железобетонной балки, армированной арматурой без её предварительного натяжения.

Алгоритм расчета основан на методе статистических испытаний, по которому осуществляется многократный расчет ситуаций нагружения конструкции. В каждом расчетном варианте прочностные характеристики материалов, постоянная и временная нагрузка принимаются случайными, путем их генерирования на ЭВМ по статистическим характеристикам.

Оценивать возможность разрушения нормальных сечений, армированных арматурой без её предварительного натяжения будем в соответствии с положениями теории риска через вероятность реализации катастрофического состояния при достижении максимального изгибающего момента от расчетных нагрузок такого его значения, при котором может произойти обрушений балки. При расчете будем исходить из предположения, что прочностные характеристики бетона и арматуры, а также действующие нагрузки являются случайными. При этом будем считать постоянными форму и геометрические размеры поперечного сечения балок, диаметры арматурных стержней и их размещение.

Статистическое моделирование используется в случаях, когда нельзя построить аналитическую модель, как функциональную зависимость выходного параметра системы от входных параметров или когда реальные испытания системы оказываются дорогостоящими или их невозможно проводить по каким-либо причинам.

Суть метода заключается в замене эксперимента с реальной системой, экспериментом с ее математическим аналогом и имитацией работы системы. Данный метод состоит из трех этапов [1]:

1. Разработка и ввод в ЭВМ моделирующего алгоритма.

2. Генерирование входных случайных величин с заданными функциями и параметрами распределения и многократное повторение опытов.

3. Статистическая обработка результатов моделирования.

Как утверждается в исследовании [3 c. 158] распределения прочностных характеристик бетона и арматуры хорошо описываются нормальным законом. Статическое описание воздействий зависит от вида учитываемых в расчетах нагрузок. Для постоянных нагрузок используют закон Гаусса, который является подходящим при нормальных условиях эксплуатации.

Математические ожидания прочности бетона, арматуры и нагрузок принимаются по нормативным значениям сопротивления материалов и действующих нагрузок, исходя из обеспеченности P=0,95. Для изгибаемых элементов конструкций в качестве критерия для расчетной оценки риска разрушения нормального сечения принимается резерв прочности по формуле 1.

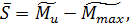
где: 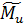 – случайные предельный изгибающий момент, воспринимаемый нормальным сечением,  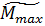– случайные значения максимального изгибающего момента в нормальном сечении балки вблизи середины пролёта.

Для расчета случайного предельного изгибающего момента используется следующий алгоритм [4]:

Выбираются случайные значения прочности бетона и арматуры. С использованием гипотезы плоских сечений по первоначально заданной деформации наиболее сжатого волокна бетона находится деформация арматуры как функция высоты сжатой зоны бетона. Через принятые зависимости между напряжениями и деформациями бетона и арматуры записывают напряжения бетона и арматуры через неизвестную высоту сжатой зоны бетона. Высота сжатой зона бетона определяется из условия равенства нулю суммы продольных сил в нормальном сечении балки. Рассчитав высоту сжатой зоны бетона, получают значение деформации арматуры. Затем проверяют максимальные деформации арматуры и наиболее сжатых волокон бетона на условие превышения максимальных значений и, если необходимо, корректируют. По полученному значению деформации наиболее сжатого волокна бетона находят предельный момент как изгибающий момент равнодействующих внутренних усилий относительно нейтральной оси сечения.

С помощью данного алгоритма определяются значения предельных изгибающих моментов M_u в соответствии со случайными параметрами прочности бетона и арматуры R_b, R_s. Выполненные многократно вычисления при разных случайных прочностных характеристиках материалов и значений нагрузки дают статистический ряд значений предельного момента и максимального изгибающего момента в нормальном сечении. Полученный ряд выравнивается с помощью вычислительных программ вероятностных расчетов.

Так как распределение предельных изгибающих моментов близко к нормальному закону, для его описания достаточно вычислить его числовые характеристики: средние и стандарты, в соответствии с которыми по закону Гаусса принимается распределение максимальных изгибающих моментов от постоянных и временных нагрузок [2; 3].

Ниже представлен алгоритм расчета риска разрушения балки в нормальном сечении при нормальном законе распределения прочностных характеристик бетона и арматуры:

Из исходных данных (геометрические размеры балки, модули деформации бетона и арматуры, параметры армирования, относительные деформации) определяются статистические характеристики по формулам 2 и 3:

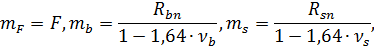
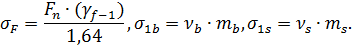
Затем генерируется массив из случайных значений прочности бетона, арматуры и нагрузки в соответствии с нормальным законом распределения.

Получают случайные значения нормативных нагрузок и сопротивлений бетона, соответствующих текущей итерации. В соответствии с трехлинейной диаграммой состояния сжатого бетона и двухлинейной диаграммой состояния сжатой арматуры выбираются деформации бетона и арматуры. Определяется предельный момент M_u в нормальном сечении по приведенному выше алгоритму. Определяется максимальный изгибающий момент в нормальном сечении M_max по формулам строительной механики. После перебора всех значений получают массив предельных моментов M_u и максимальных изгибающих моментов M_max. Определяются статистические характеристики. Определяется характеристика безопасности по формуле 4:

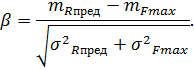
По формуле 5 определяется вероятность разрушения.