МЕТОД ПОИСКА ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ ГЕНЕТИЧЕСКОГО АЛГОРИТМА
Конференция: LXIX Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Секция: Информатика, вычислительная техника и управление

LXIX Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
МЕТОД ПОИСКА ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ ГЕНЕТИЧЕСКОГО АЛГОРИТМА
THE GENETICS’ ALGORITHM OPTIMAL PARAMETERS SEARCH METHOD
Alexandr Burdin
Head of laboratory, NPCAP, Moscow
Аннотация. В докладе доказывается необходимость поиска оптимальных значений параметров адаптированного генетического алгоритма оптимизации модульных испытательных систем. За основу разработанного метода легли принципы машинного обучения. Результаты работы позволили увеличить точность работы генетического алгоритма при оптимизации модульных испытательных систем.
Abstract. In the report proved the necessary of searching optimal values of adopted genetics’ algorithm parameters. The method based on machine learning principles. The results of the work made it possible to increase the accuracy of the genetic algorithm when optimizing modular test systems.
Ключевые слова: оптимизация; генетический алгоритм; машинное обучение.
Keywords: optimization; genetic algorithm; machine learning.
Современные тенденции развития испытательного оборудования для цифровой аппаратуры показывают перспективность использования модульного принципа при разработке. Этот подход позволяет создать систему, советующую таким критериям измерений, которые труднее реализовывать с традиционным набором аппаратуры. Постоянный реинжиниринг испытуемых приборов заставляет разработчиков аппаратуры не отставать в совершенствовании своих изделий.
Модули испытательной системы необходимо подбирать оптимально, при этом не снижая функциональных возможностей испытательного комплекса. В [1] предложена методика оптимизации модульных блочных систем на основе адаптированного, проблемно-ориентированного генетического алгоритма. В данной методике при реализации генетического алгоритма в качестве значений основных параметров таких, как размер популяции, количество особей в поколении, вероятность мутации и кроссовера, брались не оптимальные значения. Такой подход может вести к неточности работы алгоритма, и учитывая его природу (за счёт количества поколений) к неоправданно долгой работе.
Появилась потребность в методике нахождения наилучших параметров генетического алгоритма в контексте задачи оптимизации модульных испытательных систем.
В качестве меры точности работы генетического алгоритма берётся разность значения целевой функции, полученной методом полного перебора (как эталонный и дающий наиболее точный результат) и генетическим алгоритмом.
Были проведены шесть экспериментов на аналогичных друг другу задачах, отличавшихся разной размерностью пространства поиска (количеством возможных комбинаций). В качестве параметров генетического алгоритма выступали одни и те же числа таблица 1.
Таблица 1
Параметры генетического алгоритма
|
Параметр |
Значение |
|
Размер популяции |
50 |
|
Количество поколений |
50 |
|
Вероятность кроссовера |
0,80 |
|
Вероятность мутации |
0,05 |
На рисунке 1 представлен график зависимости разности значений целевой функции, полученных методом полного перебора и значением целевой функции найденным генетическим алгоритмом от размерности пространства поиска. Из графика видно, что разность растёт с увеличением размерности пространства поиска, что доказывает необходимость подстраивать параметры генетического алгоритма в зависимости от размерности пространства поиска.
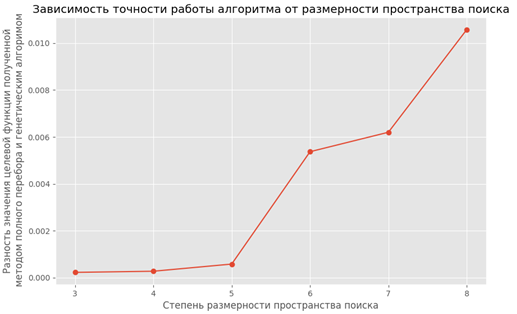
Рисунок 1. График зависимости точности работы генетического алгоритма от размерности пространства поиска
Для определения оптимальных параметров генетического алгоритма необходимо построить математическую модель ошибки, исследовать её и найти точку оптимума, где ошибка алгоритма будет минимальна.
Построить математическую модель можно при помощи классического метода полного факторного эксперимента (ПФЭ). ПФЭ даёт линейную зависимость точности алгоритма от изучаемых параметров, что может дать не корректную картину (если существует не линейная зависимость точности от параметров).
Наиболее полную модель ошибки генетического алгоритма можно построить при помощи методов машинного обучения, где модель получая на вход некоторый объём данных «обучается» (подстраивает коэффициенты). Точность полученной модели возможно оценить, используя тестовую выборку.
Данные для построения модели взяты из серии экспериментов, где входные параметры такие, как степень размерности пространства поиска, размер популяции, количество поколений в популяции, вероятность кроссовера и шанс мутации выбирались случайным образом из диапазона, представленного в таблице 2.
Таблица 2.
Значения параметров генетического алгоритма

Количество необходимых экспериментов, получено опытным путём согласно выводам, изложенным в [2], то есть количество экспериментов, при котором точность модели перестала расти (рисунок 2).

Рисунок 2. Зависимость точности модели ошибки генетического алгоритма от количества данных
Из рисунка 2, видно, что точность модели ошибки перестала расти примерно при 800 опытах.
Данные случайным образом разделены на обучающую и тестовую выборки в соотношении 0.8 и 0.2 соответственно. Построены регрессионные модели с разными степенями полиномизации и оценены их точности по коэффициенту R2 (таблица 3).
Таблица 3
Точность регрессионной модели от степени полиномизации
|
Степень полиномизации |
Коэффициент R2 |
|
1 |
0.08 |
|
2 |
0.53 |
|
3 |
0.57 |
|
4 |
0.92 |
|
5 |
0.92 |
|
6 |
0.90 |
Наиболее полно описывает точность адаптированного генетического алгоритма регрессионные модели со степенями полиномизации больше четырёх.
Далее оценены значимости параметров методом Backward Elimination со стандартным значением a = 0.05, после которого наименее статистически значимым оказался параметр вероятность кроссовера (рисунок 3).
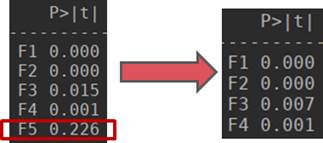
Рисунок 3. Результат применения метода Backward Elimination
Таким образом наиболее значимыми параметрами модели точности работы генетического алгоритма являются: размерность пространства поиска, размер популяции, количество поколений в популяции и шанс мутации.
В результате описанных выше действий получена математическая модель ошибки адаптированного генетического алгоритма для оптимизации модульных испытательных систем:
|
где E – ошибка алгоритма; F1 – степень размерности пространства поиска; F2 - размер популяции; F3 – количество поколений; F4 - вероятность кроссовера. |
(1) |
Критическая значимость коэффициентов: tкр.· Sкоэф. ≈ 1,48e-06.
Необходимо найти такие значения размера популяции F2, количества поколений F3, вероятности кроссовера F4 для каждой размерности пространства поиска F1, при которых ошибка E будет стремиться к нулю.
Усечённым методом Ньютона определены оптимальные значения параметров генетического алгоритма (таблица 4).
Таблица 4
Оптимальные значения параметров генетического алгоритма при разных размерностях пространства поиска
|
Степень размерности пространства поиска |
Размер популяции, шт. |
Количество поколений, шт. |
Вероятность мутации в поколении, % |
Ошибка |
|
3 |
40 |
12 |
75 |
2.06e-9 |
|
4 |
65 |
16 |
80 |
1.44e-9 |
|
5 |
39 |
63 |
65 |
1.63e-8 |
|
6 |
47 |
53 |
72 |
1.00e-8 |
|
7 |
51 |
71 |
83 |
6.35e-8 |
|
8 |
55 |
82 |
91 |
1.25e-7 |
|
9 |
59 |
89 |
62 |
9.49e-6 |
В результате проделанной работы разработана методика нахождения оптимальных параметров адаптированного генетического алгоритма для оптимизации модульных испытательных систем на основе методов машинного обучения. Данная методика позволила построить точную (относительно других методов) модель ошибки генетического алгоритма. Благодаря предложенной методике повысилось качество работы адаптированного генетического алгоритма для оптимизации модульных испытательных систем, что дало возможность разрабатывать более оптимальные испытательные системы.



