РАСЧЁТ ВИХРЯ В ВОДЕ, СМЕРЧА В ВОЗДУХЕ, ГАЛАКТИЧЕСКОГО ТОРНАДО В НАЧАЛЕ ОБРАЗОВАНИЯ

CALCULATION OF A VORTEX IN WATER, A TORNADO IN THE AIR, A GALACTIC TORNADO AT THE BEGINNING OF FORMATION

Valery Dmitriev

Doctor of Technical Sciences, Chief Researcher, JSC "NPO "SPLAV" named after Ganichev, Russia, Tula

Аннотация. Рассматривается вихревое движение воды, воздуха, космического газопылевого облака. Приводится расчет указанных течений, в частности, образование галактик. Для получения систем уравнений используется программа аналитических вычислений «МАТКАД»

Abstract. The vortex motion of water, air, and a cosmic gas-dust cloud is considered. The calculation of these flows, in particular, the formation of galaxies, is given. To obtain systems of equations, the analytical computing program "MATKAD" is used

Ключевые слова: Космология; Вселенная; Большой взрыв; газ, галактики; Земля; вода; волны-убийцы; «Сцила и Харибда»; планеты; туристы.

Keywords: Cosmology; Universe; Big Bang; gas, galaxies; Earth; water; killer waves; "Scylla and Charybdis"; planets; tourists.

Вихревое движение широко распространено в природе. Аналитический метод расчета вихревого движения в работе [2] не учитывают характера изменения параметров как в ядре вихря, так и на его периферии. Ниже излагается  более подробный аналитический метод расчета параметров вихря с использованием программы аналитических преобразований «МАТКАД».

В общем случае для расчета необходимо использовать уравнения газовой динамики [8,10].

Система уравнений стационарного движения газа в интегро-дифференциальной форме приведена в работе [5] и имеет для объема W с поверхностью S_п следующий вид:

Уравнение сохранения массы

                                                                                                       (1)

Уравнение сохранения импульса

,                                                                           (2)

где

                                                                                                                                              (3)

- потенциальная сила, действующая на единицу объёма;

 -в соответствии с     (7).

Уравнение сохранения энергии

                                                             (4)

Уравнение сохранения момента импульса

.                                                                                       (5)

Это уравнение описывает вихревое течение жидкости.

Уравнение состояния

,

где       t – время; q – плотность газа;

v^z – скорость;

 – скорость поверхности Sп;

р – давление;

k – отношение теплоемкостей;

е – удельная внутренняя энергия;

Т – температура,

,

c_v- теплоемкость газа при постоянном объеме

Е – удельная полная энергия,

,

,

где       G_es – метрический тензор;

А_ez – тензор скоростей деформаций.

Тензор скоростей деформаций вычисляется по формуле

,        

m₁, m₂ – коэффициенты динамической вязкости (первая и вторая вязкости)

Градиент температуры определяется по формуле

.

Для решения разных задач физики используются разные системы отсчёта - координат и времени.

Система уравнений движения газа и взаимодействующих тел должна быть дополнена информационным уравнением о метрике используемой координатной сетки [5], необходимой для нахождения элементарных площади и объема.

,  ,                                                                                           (6)

,                                                                         (7)

,    .                                                                                       (8)

Здесь

                                                                                                            (9)

– связь между используемой и базисной системами координат;

.                                                                                                  (10)

δ_σσ – символ Кронекера.

Информационное уравнение для метрики отражает получение и преобразование информации в используемой системе отсчета. Например, в случае применения телескопа углы  в горизонтальной и вертикальной плоскостях φ и θ от плоскостей отсчета выдаются в зависимости от положения  угловых датчиков электронной системы слежения за звездой. Расстояние до звезды r может быть определено в результате замера яркости звезды (при известном классе звезды) фотометром.

Считаем, что в газе не действуют вращающие моменты внешних сил и . Тогда уравнение сохранения момента импульса в стационарном случае примет вид 

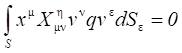.                                                                                                 (11)

Для выполнения данного уравнения в любом месте и по любой поверхности должно быть

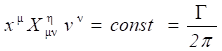, или r´v=G¤2p.                                                                      (12)

Тогда Г/2p можно вынести из-под знака интеграла и ввиду уравнения сохранения массы

                                                                                                  (13)

уравнение (11) будет тождественно выполняться.

Данное уравнение описывает вихрь. В цилиндрической СК r, φ, z с осью z по w0  проекция на ось вращения w0 из (16) равна

.                                                                                             (14)

Где Г-циркуляция скорости, r - расстояние до оси вращения, v^t -тангенциальная составляющая скорости газа в вихре.

При r=0 из уравнения (16) следует v^t=¥ . Поэтому используем другое решение уравнения(11)

                                                                                     (15)

как векторное произведение двух параллельных векторов. При r=rc=r₀ =R имеем  из (14)

.                                                                                              (16)

При      r<r₀

v_t =wr ,                                                                                                              (17)

где r₀ –радиус ядра вихря (см. рисунок).

Используем для расчета условие 

Преобразуем уравнения (1)-(5), используя (6)-(10).

Выносим qv^e  за скобки, используем уравнение  и заменяем dW по (7).

Тогда получаем уравнение сохранения энергии в стационарном случае при неподвижной поверхности

                                                                                   (18)

Чтобы уравнение (18) тождественно выполнялось при всех объёмах жидкости с поверхностью S , должно быть (при вынесении выражения в квадратных скобках за знак интеграла)  ввиду уравнения (1)

                                                                                    (19)

Или         

- Уравнение Бернулли для газа.

Для импульса имеем в стационарном случае

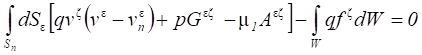.                                                                    (20)

Используем уравнение  и заменяем dW по (11).

Тогда получаем уравнение сохранения импульса в стационарном случае при неподвижной поверхности

                                                                               (21)

Чтобы уравнение (21) тождественно выполнялось при всех объёмах жидкости с поверхностью S , должно быть ввиду уравнения

,(теорема Остроградского при φ=const)

 равной постоянной  с плюсом или минусом

                                                                                          (22)

При неучете трения μ₁=0,

Знак - используем при расчете течения газа в случае r<r0 или в других обозначениях r<R.

Постоянную i1 находим из условия в центре вихря r=0. Тогда по (17) v=0 и

                                                                                                         (23)

Постоянную i2 находим из условия на границе  вихря r=r_a. Тогда по (17) v=v_а и

                                                                                          (24)

Полученные уравнения (19)- (24) позволяют рассчитать все параметры вихря как в ядре вихря, так и за его пределами.

Для параметров на границе ядра имеем

.

Для параметров в центре вихря

Дальше для проведения расчетов используем программу аналитических вычислений в МАТКАДе [6]. Использование программы аналитических вычисления позволяет автоматически получать уравнения физического изменения состояния изучаемого объекта используя в качестве исходных данных математические выражения физических законов. При этом происходит сокращение времени расчета по сравнению с расчетом методом численного интегрирования в тысячи раз. Ниже автоматические аналитические преобразования выделяются прямым латинским шрифтом, стрелка показывает результат преобразования, прямоугольная точка показывает, что в это место должно вставляться следующее выражение.

Проведем расчет Галактического вихря в момент образования 13 млрд. лет назад.

Галактическое облако подвержено силе тяготения, определяемой по формуле для гравитационного потенциала[7]

Проводим аналитические вычисления.

 уравнение для нахождения q0*

0= 

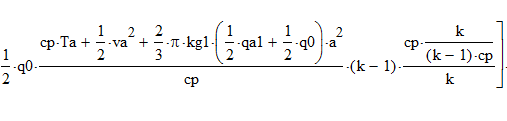
.                                                  (24а)

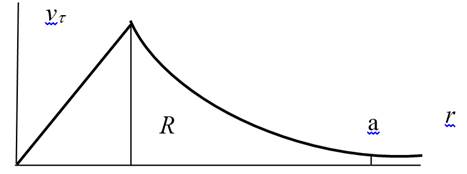
Рисунок. Изменение тангенциальной скорости v_τ по радиусу в вихре

Исходные данные в СИ: радиус Галактики a, постоянная тяготения kg1, радиус ядра R1, тангенциальная скорость в ядре vR, температура в пространстве Ta, плотность в пространстве qa, теплоемкость межгалактического газа(плазмы) при постоянном давлении cp, отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме k, давление межгалактического газа pa [3].

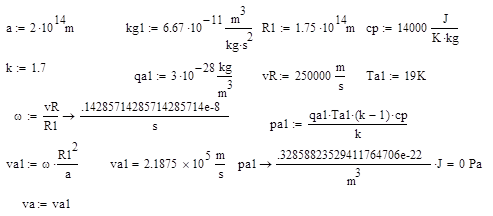
Подставляя исходные данные в (24а), получаем кубическое уравнение(без обозначения размерностей для уменьшения громоздкости уравнений):

1+v1*q0+v2*q0²+v3*q0³ =0.

Решая это кубическое уравнение по программе в МАТКАД, получаем три значения q0.

Берем третье значение, так как первые два не соответствуют физическому смыслу рассматриваемой задачи

Далее находим параметры

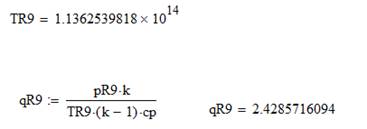
Как видно по результатам расчета, в центре галактического торнадо вследствие действия сил тяготения образуется ядро с повышенной плотностью q09, с очень высоким давлением p09, с очень высокой температурой T09. Такие параметры в центре Галактики привели в дальнейшем к образованию в центре «черной дыры».

Для сравнения результатов расчета с опытными данными вычислим массу Галактики, считая Галактику тонким эллиптическим диском с толщиной в 100 раз меньшей, чем диаметр, и считая радиус и толщина Галактики 13млрд. л. н. были вследствие общего расширения Вселенной в 10⁶ раз меньшими (что соответствует возникновению Галактического торнадо 12 млн. лет после Большого Взрыва) [3].

В результате расчета получаем

Как видно, опытные данные согласуются с расчетными.

Таким образом, вследствие неустойчивости при больших относительных скоростях трехмерного течения газа образуются парные вихри, приводящие к возникновению структуры Галактик [1], [5]. Время образования галактики определяется скоростью распада вихря (например, для галактики Большое Магелланово облако по результатам математического моделирования по разработанной программе расчете трехмерного потока методом Годунова [5] – (13000-130000)лет).

Для воздушного вихря (смерча) Земли гравитационные силы не учитываем и положим k_g=0, П=0

Проводя аналитические преобразования, получаем

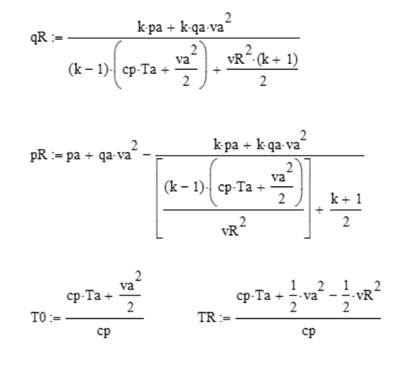
Проводим расчет при исходных данных, полученных из метеорологических наблюдений на Земле, в СИ:

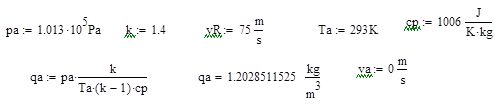
Вычисления по полученной системе уравнений дают (без обозначения размерностей) значения параметров смерча:

Опытное значение давления по данным исследователей США имеет значение в центре воздушного вихря на Земле (смерча) [9] Р0=0.95*10⁵ Па.

Таким образом в центре смерча создается пониженное на 5% давление. Полученные расчетные данные согласуются с опытными данными.

Сравнивая qa и q0 видим, что плотность на периферии смерча и в центре смерча мало отличаются. Поэтому данное решение можно применить для расчета водного вихря, плотность воды которого постоянна. Таким образом, в центре водного вихря создается пониженное на 5% давление.

Такой же результат дает расчет по программе на ЭВМ численного расчета трехмерного газового потока методом Годунова [4], но требует наличия мощного компьютера.

Выводы

При образовании галактик вследствие больших относительных скоростей плазменного облака, полученных в начале «большого взрыва», происходит образование вихря вследствие неустойчивости трехмерного течения. В центре вихря (галактического торнадо) образуется под действием сил тяготения область с высокой плотностью и температурой. В дальнейшем под действием сил тяготения в центре этой области образуется «черная дыра».

Расчет вихревого движения газовой сферы Земли и других планет показывает, что в центре вихрей газовой сферы планет(смерчей) имеется область пониженного давления, что приводит к всасывающему действию смерча, поднятию им различных предметов. Так, по сообщению областной газеты в 1948 году смерч, образовавшийся (по наблюдению автора) в районе г. Болохово и двигающийся вдоль реки Упы, при достижении Московского вокзала в г. Туле скинул с рельс железнодорожный подъемный кран весом 200тс, а затем распался.

Имеются смерчи и на других планетах, например, красное пятно в газовой сфере Юпитера [3].

Гидросфера Земли также подвержена вихреобразованию.

Водные вихри на океанах аналогично являются причиной многих кораблекрушений вследствие образования волн-убийц (например, в районе Бермудского треугольника).

Меньшие водные вихри на морях вследствие наличия пониженного давления в центре вихря, могут поглощать лодки с людьми, что фиксируется многими легендами как заглатывание морскими чудовищами (миф о «Сцилле и Харибде»).

Еще меньшие вихри образуются в быстрых реках. Так как в центре речных вихрей понижается давление, то вихри затягивают попавшие в них предметы. Как подтверждается многочисленными туристами-водниками, попавшие в водный вихрь люди засасываются до дна реки и затем выбрасываются на некотором расстоянии на поверхность.

Полученные зависимости могут быть использованы в инженерных расчетах.