Модель турбулентного переноса и физической коагуляции капель эмульсий на стенке канала

MODEL OF TURBULENT TRANSPORT AND PHYSICAL COAGULATION OF THE DROPLETS OF THE EMULSION INTO THE CHANNEL WALL

Anatoly Laptev

Doctor of technical Sciences, Professor Kazan state power engineering University, Russia, Kazan

Marat Basharov

Candidate of technical Sciences Deputy General Director maintenance and engineering JSC TANECO, Russia, Nizhnekamsk

Работа выполнена в рамках базовой части государственного задания в сфере научной деятельности (№13.6384.2017/БЧ).

Аннотация. Рассмотрен турбулентный перенос тонкодисперсной фазы в жидкостях и осаждение на стенки канала. Записано дифференциальное уравнение конвективной диффузии частиц с учетом турбулентного переноса и осаждения на стенку. Получено выражение для расчета скорости турбулентной миграции частиц к стенке канала. Даны результаты расчетов коэффициента турбулентной миграции и эффективности разделения эмульсии.

Abstract. Considered turbulent transfer of finely dispersed phase in the liquid and deposition on the channel walls. Recorded differential equation of convective diffusion of particles subject to turbulent transfer and deposition on the wall. The resulting expression for the rate of turbulent migration of particles to the channel wall. The results of calculations of the coefficient of turbulent migration and the efficiency of separation of the emulsion.

Ключевые слова: эффективность; контактное устройство; сепарация; турбулентный перенос; дисперсная фаза.

Keywords: efficiency; contact device; separation; turbulent transfer; dispersed phase.

Введение

При выборе конструкций сепарирующих устройств, для заданных условий проведения процесса, расчет эффективности выделения дисперсной фазы из жидкости является основной задачей. Эффективность может быть определена по содержанию дисперсной фазы в жидкости на входе в аппарат очистки и на выходе из него по известному выражению:

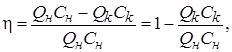                                                                                               (1)

где  - концентрация частиц, кг/м³;  - расход жидкости; м³/с; «н», «к» - начальное и конечное значения. Обычно для аппаратов принимается  Тогда .

Выделение дисперсной фазы из жидкости может происходить в результате гравитационного, диффузионного, турбулентного, инерционного осаждения. Принцип работы большинства промышленных аппаратов основан на совмещении различных механизмов осаждения. На эффективность сепарации влияние каждого из  механизмов зависит от различных параметров, таких как размер и плотность  частиц, физические свойства среды, условия протекания процесса.

Общая эффективность при одновременном действии нескольких взаимно не связанных механизмов и при очистке в нескольких последовательных аппаратах (зонах), находится по правилу:

                                                                                                     (2)

где  - эффективность сепарации за счет i-го механизма или i-м аппарате(зоне).

Уравнения переноса тонкодисперсной фазы в турбулентном потоке

Как известно, расчет осаждения крупных дисперсных частиц при ламинарном режиме не представляет значительных трудностей. Гораздо сложнее определить эффективность при турбулентном режиме переноса тонкодисперсной фазы (используется термин - турбулентное осаждение).

Проблема математического моделирования взвешенных частиц в турбулентных потоках является важной и актуальной как для фундаментальной науки, так и для практических приложений для расчета различных технических и технологических устройств. Фундаментальные исследования в этой области были выполнены Колмогоровым А.Н., Левичем В.Г., Кучановым С.И., Рахматуллиным Х.А., Нигматулиным Р.И., Кисловской М.Д. и др. Разработаны теоретические основы и модельные представления. Левич В.Г. и Кучанов С.И., оценили величину дополнительной диссипации энергии, обусловленную наличием в турбулентном потоке взвешенных частиц, и пришли к выводу, что из – за практически полного увлечения частиц жидкостью, инерционная диссипация в жидкости незначительна в отличии от движения частиц в газах. Т.е. определяющим механизмом в данном случае является турбулентный перенос частиц. По данным различных исследователей наличие в потоке твердых частиц может как уменьшать его турбулентность, так и увеличивать. В ламинарных течениях частицы могут служить своеобразными дискретными турбулизаторами и тогда турбулентный режим наступает при числе Рейнольдса в несколько раз меньшем, чем для однофазных сред.

Примером одной из прикладных задач является гидротранспорт дисперсной фазы. В таком случае требуется минимальное осаждение и прилипание транспортируемых частиц к стенкам канала. Обратной задачей может служить пример разделения эмульсий и суспензий в аппаратах, когда требуется максимальная эффективность осаждения с минимальными затратами и габаритами аппаратов. Большинство аппаратов являются проточными и при проведении таких процессов они должны работать при ламинарном режиме несущей фазы (песколовки, нефтеловушки, и др.). Однако в этих аппаратах при больших расходах смеси не всегда возможна организация «чистого» ламинарного движения. В крупногабаритных аппаратах неизбежно возникают циркуляционные контуры, вихреобразования различного масштаба и т.д. Эти явления могут быть вызваны входными неравномерностями, градиентами температур (на стенке и в ядре потока), градиентами концентраций и другими возможными неустойчивостями потоков. Турбулентность так же может быть организована за счет специальных конструкций аппаратов, например, в гидроциклонах. В отстойниках же, турбулентность «подавляется» за счет тонкослойных модулей (наклонных перегородок и др.). Известно, что эффективность таких аппаратов повышается в несколько раз. Однако и в таких аппаратах при вынужденном повышении нагрузки может наступить переход к турбулентному режиму. В отличии от гидротранспорта в таких отстойниках поверхность сепарирующих элементов (модулей) должна хорошо смачиваться и удерживать дисперсную фазу (разделение эмульсий), а так же твердую дисперсную фазу с минимальным срывом и уносом.

Далее рассмотрен подход Ф.П. Заостровского и К.Н. Шабалина (1951-1953г.г.) и развитый Е.П. Медниковым, А.Ю. Иваненко, Г.М. Островским, С.И. Кучановым и другими авторами [1-4], когда перенос тонкодисперсной фазы рассматривается как разновидность диффузионного процесса и для его описания пользуются уравнениями из теории массопередачи и турбулентной миграции частиц.

Для определения эффективности контактного устройства при сепарации ниже приведено уравнение конвективного массопереноса частиц. В качестве примера рассмотрен турбулентный режим потока жидкости, который на входе контактного устройства (например, прямоугольный канал) имеет концентрацию тонкодисперсной фазы . В процессе движения жидкости в канале за счет турбулентной диффузии происходит миграция дисперсной фазы всторону стенки. Использованы следующие известные допущения: диаметр частиц d_ч мал по сравнению с масштабом несущих их пульсационных вихрей; полидисперсность учитывается пофракционно; при концентрации дисперсной фазы С< 0,2 кг/м³  частицы не соударяются и не коагулируются друг с другом; вторичный срыв частиц со стенки канала после осаждения незначителен. Потому в зависимости свойств от разделяющих фаз выбирается материал стенок хорошо удерживающие частицы. Разделяющие сепарирующие модули монтируются под некоторым углом (40-60°) и осевшие частицы сползают вниз, а при разделении эмульсий образуется подвижная пленка, которая за счет разности плотностей фаз выводится из разделяющего модуля.

Уравнение стационарного переноса дисперсных частиц в жидкости запишется в виде:

                                                           (3)

где x, y, z - пространственные координаты, м; D_d - коэффициент турбулентной диффузии частиц, м²/с.

При турбулентном движении жидкости за пределами пограничного слоя броуновской диффузией обычно  пренебрегают, поскольку ее роль очень мала.

Для решения уравнения (3) прежде всего, необходимо иметь трехмерное поле скорости - ,, и функцию для коэффициента турбулентной  диффузии частиц  (x, y, z). Тогда при заданных значениях начальных и граничных концентраций из решения уравнения (3) можно вычислить распределение концентраций частиц по координатам х, y, z. Как отмечается в работе [3] задать концентрацию дисперсных частиц на стенке канала (сепарирующих элементов) затруднительно из-за некоторых неопределенностей. Поэтому используем известный подход, когда массоперенос компонента в уравнении переноса учитывается в виде локального или среднего объемного источника массы.

Источник массы в общем виде записывается в форме:

                                                                                                         (4)

где M - поток частиц, кг/с; dV - элементарный объем контактного устройства, м³; j - удельный поток частиц к стенке у ее поверхности к площади dF, кг/(м²с); F - площадь контакта жидкости со стенками канала, м².

Как отмечено А.Ю. Иваненко и Г.М. Островским, одним из простых вариантов моделирования является аналогия с коэффициентами тепло- и массоотдачи и вводится некий коэффициент «частицеотдачи» , который тождественен скорости миграции частицы к стенке.

Поток массы дисперсной фазы к стенке записывают в форме аналога уравнения массоотдачи

,                                                                                                           (5)

где - скорость турбулентной миграции (коэффициент переноса), м/с; - концентрация частиц в ядре потока, принимается средней по поперечному сечению, кг/м³. Известно, что в теории массопередачи движущая сила массоотдачи записывается в виде  (или ). Однако, при осаждении частица, достигающая стенки канала и прилипая к поверхности (полностью поглощающие стенки), как бы исчезает из несущей фазы и поэтому .

Коэффициент скорости турбулентного осаждения частиц  характеризует интенсивность осаждения частиц из турбулентного потока жидкости на стенках, т.е. количество частиц (весовое или численное), осаждающихся из потока жидкости на 1м² стенок за 1 сек, отнесенное к единичной концентрации частиц [3].

С учетом вышеизложенных допущений и оценки пространственно-временных масштабов явлений переноса, уравнение (3) для плоскопараллельного канала, получит вид:

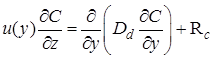,                                                                                             (6)

а для цилиндрического канала:

,                                                                                           (7)

где - радиальное расстояние до оси трубы, м; z- продольная координата (в направлении движения жидкости), м; y - поперечная координата к стенке канала, м; u(r) - скорость течения среды, как функция радиуса канала, м/с.

Определение коэффициента турбулентного переноса

При обтекании потока с дисперсными частицами на поверхности контактного устройства дисперсная фаза сепарируется (осаждается)  за счет различных механизмов. При осаждении  капель на поверхности  канала или насадки будет образовываться пленка.

В турбулентном потоке на безынерционные и слабоинерционные дисперсные частицы будет действовать эффект турбулентной миграции. Поскольку инерционные дисперсные частицы не подвержены влиянию линий тока жидкости и не увлекаются турбулентными пульсациями среды, то их движение можно считать прямолинейным. Эффективность осаждения инерционных дисперсных частиц на контактном устройстве будет определяться в основном их геометрическими размерами. В свою очередь слабоинерционные дисперсные частицы можно разделить на две группы. Первая – это частицы, успевающие за время релаксации достичь поверхности и осесть на ней. Вторая – частицы, которые подвержены влиянию течения жидкости, за время сближения с контактным устройством они не успевают осесть на его поверхности  [3].

Физической основой появления миграции частиц в сторону стенки является то, что мелкая, легко увлекаемая турбулентной средой частица, в ходе движения среды совершает идентичное движение практически с тем же ускорением, что и среда. Перемещаясь по потоку, тонкодисперсная фаза на том или ином этапе своего движения достигает пристеночной области и, когда расстояние до стенки становится равным радиусу частицы, касается ее и осаждается на ней, если поверхность стенки удерживает частицы. Число Вебера в случае движения и коагуляции капель в эмульсиях We < 10, т.е. дробление капель не происходит.

Коэффициент скорости миграции  характеризует интенсивность осаждения частиц из турбулентного потока на стенку канала  или, где– удельный поток частиц к стенке, кг/(м²с);– средняя по поперечному сечению концентрация частиц, кг/м³ [3].

Выражение  является аналогом известного уравнения массоотдачи , где – коэффициент массоотдачи, м/с; ΔС - движущая сила массоотдачи (разность концентраций в ядре потока и на поверхности).

Для очень малых частиц [1-4], их движение практически ничем не отличается от движения несущих турбулентных вихрей среды и тогда = , где , - коэффициенты турбулентной диффузии частиц и среды, м²/с.

Удельный поток частиц по аналогии с первым законом Фика записывается в виде:

,                                                                                                        (8)

где  - коэффициент броуновской диффузии, м²/с.

Сопротивление переносу частиц в пристенном слое, с учетом броуновской и турбулентной диффузии, имеет вид [2]:

,                                                                                                   (9)

где  - безразмерная плотность потока частиц к стенке; δ- толщина пограничного слоя, м.

Коэффициент турбулентной диффузии  частиц для частиц II группы, т.е. частично увлекаемых турбулентными пульсациями среды [1-4], равен:

                                                                                                       (10)

где - угловая частота энергоемких пульсаций, с^-1; - время релаксации частицы, с; - коэффициент турбулентной диффузии, м²/с.

Выражения для частоты энергоемких пульсаций и времени  релаксации имеют форму:

                                                                                                (11)

где - динамическая скорость, м/с;   – эквивалентный радиус канала, м; – диаметр частиц, м; - плотность частицы, кг/м³; – коэффициент динамической вязкости среды, Па∙с;.

Обычно с небольшой погрешностью допускают , где - коэффициент турбулентной вязкости среды, м²/с. 

Турбулентная миграция частиц

Согласно одному из положений (гипотезе) свободного инерционного движения частиц из турбулентного потока к стенке, в пристеночной области взвешенные частицы из-за приобретенной от вихрей кинетической энергии преодолевают вязкое трение до самой стенки [3]. Вблизи вязкого подслоя происходит затухание турбулентности (по модели Ландау-Левича и в вязком подслое происходит постепенное затухание турбулентности), а взвешенные частицы продолжают свой путь в силу инерции через вязкий подслой вплоть до стенки. К тому же, при движении турбулентного потока с дисперсной фазой на поверхности канала за счет осаждения частиц образуется шероховатость, выступы которой могут превышать толщину вязкого подслоя.

На основании вышесказанного можно пренебречь переносом в вязком подслое и рассматривать перенос только в буферной и турбулентной областях.

Тогда сопротивление переносу частиц получит вид:

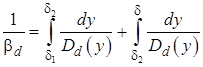.                                                                                           (12)

где   - толщина вязкого подслоя, м; -толщина буферной (переходной) области, м.

С функциями Дайслера   после интегрирования (12) получено

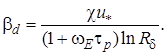                                                                                                  (13)

где - константа турбулентности;  - безразмерная толщина пограничного слоя.

Динамическая скорость на стенке круглого канала: , а в хаотичном насадочном слое:   [5], где - коэффициент гидравлического сопротивления;  - число Рейнольдса; -средняя скорость среды, м/с; - эквивалентный диаметр насадки, м.

На рис.1. показаны результаты расчетов коэффициента переноса частиц (13) в зависимости от их диаметра и плотности. Видно, что с увеличением диаметра и плотности частиц скорость турбулентного переноса снижается. Для крупных  частиц необходимо учитывать и силу тяжести.

Рисунок 1. Зависимость коэффициента переноса от диаметра частиц  1 - ρ_ч = 2650 кг/м³; 2 - ρ_ч = 7560 кг/м³; 3 - ρ_ч=1100 кг/м³; μ_ж = 0,656 ×10^-3Па·с;  = 0,005 м/с; δ = 0,01 м. Расчет по уравнению (13)  (без учета силы тяжести). Осаждение на пластину.

Пример расчета эффективности сепарации (процесс физической коагуляции  капель эмульсии на стенке).

Система: вода при  температуре   с дисперсной фазой (каплями) диаметром , м (1мкм): ; концентрация частиц  кг/кг. Движение смеси в трубе диаметром  м; расход смеси м³/с; средняя скорость  м/с. Число Рейнольдса .

1) Гладкие стенки. Коэффициент сопротивления ; динамическая скорость  м/с;  безразмерная толщина пограничного слоя ; коэффициент переноса м/с.

2) Стенки с полным проявлением шероховатости. Коэффициент сопротивления ; динамическая скорость  м/с; ;  м/с.

Из решения уравнения  (7) с граничными условиями: z=0; ; ; при , находим концентрацию частиц на выходе из трубы.  При длине 10 м получаем  1)  кг/кг, 2)  кг/кг.

Эффективность сепарации  1) ; 2) ,

т.е. в первом случае на стенке за счет турбулентной миграции осело 65% частиц, а во втором 77%.

В качестве следующего примера на рис. 2  даны результаты  расчетов эффективности коагуляции капель на поверхность хаотичных насадочных элементов, расположенных в канале перед подачей в отстойник.

Рисунок 2. Зависимость эффективности коагуляции капель воды в ШФЛУ от длины насадочного слоя (насадка: кольца Рашига 15х15х2 мм)1 – Re_Э= 500; 2 – Re_Э= 1000

На насадке происходит слияние капель, а затем на выходе  из канала, т.е. на входе в отстойник, с насадки происходит отрыв дисперсной фазы в виде капель с значительно большим диаметром, чем в исходной эмульсии. Таким образом насадочный коагулятор значительно повышает эффективность разделения эмульсии в отстойнике.

Выводы

В данной работе рассмотрен процесс турбулентного переноса  тонкодисперсной фазы в жидкостях и осаждение частиц на стенках канала и хаотичной насадки. Для определения профиля частиц в канале, с учетом осаждения на стенки, использованы дифференциальные уравнения с частными производными (двумерная задача), где турбулентный перенос дисперсной фазы в объеме среды учитывается коэффициентом турбулентной диффузии частиц, а осаждение на стенку в виде объемного источника массы. В объемном источнике основным параметром является коэффициент скорости турбулентной миграции частиц к стенке канала. Коэффициент турбулентной миграции определен с применением модели пограничного слоя Дайсера и аналогии переноса несущих турбулентных вихрей и частиц. Даны результаты расчетов коэффициентов турбулентного переноса частиц и эффективности сепарации эмульсии. Внедрение отстойников с каогуляторами  в промышленности   показывает адекватность  представленной математической  модели [6,7].