Составление кластера при обучении школьников решению тригонометрических уравнений

The preparation of the cluster to teaching the solution of trigonometric equations

Natalia Sukhanova

the candidate of pedagogical Sciences, associate Professor, Budgetary institution of higher professional education "Surgut state pedagogical University", Russia, Surgut

Diana Tulemisova

bachelor direction of preparation "Pedagogical education" (focus Maths) Budget institution of higher professional education "Surgut state pedagogical University", Russia, Surgut

Аннотация. В статье представлена возможность применение метода построения кластера при обучении школьников решению тригонометрических уравнений. Данный прием реализует обобщение и систематизацию изученного материала, дает возможность визуализировать результат деятельности школьника по поиску решения тригонометрического уравнения.

Abstract. The article presents the possibility of application of the method of building a cluster to teaching the solution of trigonometric equations. This technique implements a generalization and systematization of the studied material, gives the possibility to visualize the result of the activities of the student to find solutions to trigonometric equations.

Ключевые слова: тригонометрические уравнения, решение тригонометрического уравнения, кластер, обобщение, систематизация.

Keywords: trigonometric equations, solution of trigonometric equations, cluster, generalization, systematization.

Тригонометрические уравнения одна из сложных тем в школьном курсе алгебры и начал анализа. Несмотря на этот аспект, тригонометрические уравнения являются интереснейшей темой элементарной математики, развивающейся на протяжении долгого времени. Данные уравнения имеют свои отличительные особенности, которые подразделяют уравнения на определенные виды. Следовательно, для каждого из видов можно применить те или иные методы и приемы решения.

Тригонометрическое уравнение (ТУ) – уравнение, содержащее переменную под знаком тригонометрических функций [1, с. 36]. Решение ТУ делится на два этапа: тождественные преобразования уравнения, с целью получения его простейшего вида и решение полученного простейшего тригонометрического уравнения.

На современном этапе развития наук в область применения тригонометрии входят: навигация, анализ финансовых рынков, электроника, медицина, химия, архитектуры и т.д. Поэтому изучение ТУ актуально для старшеклассников.

Обобщим изученный теоретический материал и покажем связь единичной окружности с графиком тригонометрической функции (рис. 1).

Систематизирующий эффект представленного на рисунке 1 кластера состоит в том, что на нем оказались соединенными различные методы решения уравнения: метод единичной окружности, метод использования графика тригонометрической функции, метод работы с памятками, как с опорным конспектом [2]. Этот аспект позволит реализовать последовательное построение анализа исследуемой проблемы (поиска решения тригонометрического уравнения) с последующей систематизацией полученных результатов.

Такая визуализация учебного материала позволит кажущийся сложный материал сделать доступным для школьника.

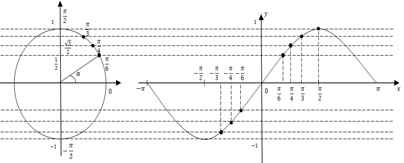
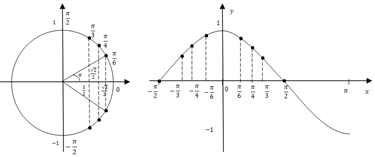
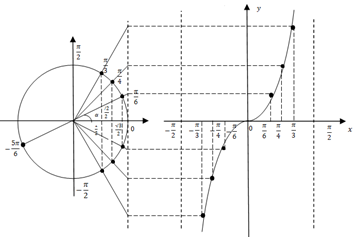
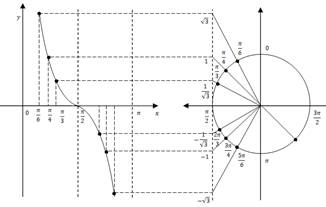
Рисунок 1. Простейшие тригонометрические уравнения

В математической литературе описывается набор специальных методов и приемов решения ТУ. Изучая их основные виды целесообразно постепенно производить обобщение типизации ТУ, которую мы предлагаем представить следующим кластером (рис.2).

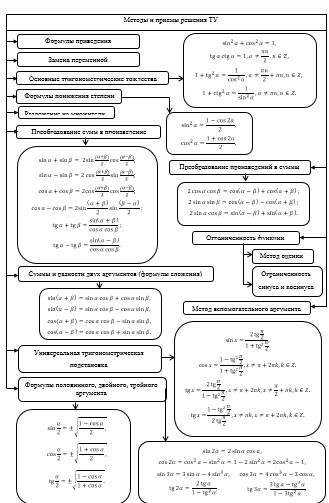
Рисунок 2. Методы и приемы решения тригонометрических уравнений

Процесс решения ТУ непрост и многообразен. Выбор метода для их решения определен сложностью тригонометрического выражения, входящего в уравнение, и уровнем математических знаний и умений самого решающего этого ТУ. Составление кластера позволяет визуализировать учебный материал, обеспечивая включенность обучающегося в процесс обобщения и систематизации процесса поиска решения тригонометрического уравнения.