КАК РАЗВИВАТЬ ИССЛЕДОВАТЕЛЬСКИЕ НАВЫКИ УЧАЩИХСЯ ЧЕРЕЗ ПРОБЛЕМНОЕ ОБУЧЕНИЕ И ПРИМЕНЕНИЕ МЕТОДОВ РАЗВИТИЯ КРИТИЧЕСКОГО МЫШЛЕНИЯ

HOW TO DEVELOP RESEARCH SKILLS OF STUDENTS THROUGH PROBLEM-BASED LEARNING AND APPLICATION OF CRITICAL THINKING DEVELOPMENT METHODS

Bakhtygul Bismildinova

Mathematics teacher, KSU "Jana Kalinskaya basic comprehensive school" of education department of Pavlodar region, the education department of Pavlodar region, Republic of Kazakhstan, Jana cala

Bibigul Bismeldinova

Mathematics teacher, master of natural sciences, Nazarbayev Intellectual school of Physics and Mathematics, Republic of Kazakhstan, Nur-Sultan

Maya Ospanova

Mathematics teacher, Nazarbayev Intellectual School of Chemistry and Biology, Republic of Kazakhstan, Pavlodar

Аннотация. Исследование направлено на то, чтобы показать, что математическое образование, основанное на проблемном обучении, реализованном на методах развития критического мышления − один из лучших способов формирования навыков мышления высокого порядка, исследовательских навыков и развития критического мышления. Целью исследования является, определить влияние проблемного обучения и методов развития критического мышления на развитие у учащихся навыков анализа, синтеза, оценки, критического мышления и исследовательских навыков.

Учащиеся 7 класса, отобранные с различных школ, имеют различный уровень учебных и познавательных навыков. Начальный анализ определил затруднения учащихся 7 класса при выполнении заданий на исследование, анализ, синтез и оценку. Результаты исследования  показали, что задания, направленные на исследование и проблемные задания, развивают у учащихся мышление высокого порядка, исследовательские навыки, развивают логическое, критическое и абстрактное мышление, приобретают глубокие и фундаментальные знания, которые творчески используются в практической деятельности, а также дают мотивацию к достижению успеха. 

Abstract. The study aims to show that mathematical education based on problem-based learning and implementation of the methods of developing critical thinking is one of the best ways to form high-order thinking skills, research and  critical thinking skills. The purpose of the study is to determine the impact of problem-based learning and the methods of developing critical thinking on the development of students' skills in analysis, synthesis, evaluation, critical thinking and research skills.

Students in grade 7 selected from various schools have a different level of educational and cognitive skills. The initial analysis identified the difficulties of students in grade 7 when completing tasks for research, analysis, synthesis and evaluation. The results of the study showed that tasks aimed at research and problem solving develop high-order thinking, research skills, develop logical, critical and abstract thinking. Moreover, such tasks acquire deep and fundamental knowledge that is creatively used in practical activities and also give students motivation to further success.

Ключевые слова: проблемное обучение; методы критического мышления; исследовательские навыки; анализ, синтез; оценка; обучение математики.

Keywords: problem-based learning; critical thinking methods; research skills; analysis; synthesis; evaluation; teaching mathematics.

Критическое мышление относится к навыкам мышления высокого порядка. В настоящее время, в огромном потоке информации критическое мышление становится необходимым для развития ученика, обладающего ценностно-смысловыми, общекультурными, учебно-познавательными, информационными, коммуникативными   компетенциями и компетенцией личностного самосовершенствования. В данном исследовании мы хотим показать, что математическое образование, основанное на проблемном обучении, реализованном на методах развития критического мышления − один из лучших способов формирования навыков мышления высокого порядка и развития критического мышления.

Начальные наблюдения, мониторинг учебных достижений учащихся и результаты психологического анализа в 7 классах показало, что учащиеся, отобранные с различных школ, имеют различный уровень учебных и познавательных навыков. А также результаты показали, что учащимся, оказавшихся в новой образовательной среде и коллективе, обучение вызвало определенные сложности. Решая данные проблемы в рамках исследования в действии, мы реализовали проблемное обучение, применяя методы развития критического мышления. Данное исследование направлено на определение влияния проблемного обучения и методов развития критического мышления на развитие у учащихся навыков анализа, синтеза, оценки, критического мышления и исследовательских навыков. Результаты этого исследования показывают, что: через проблемное обучение формируется навыки анализа, синтеза и оценки; формируются исследовательские навыки; формируются умения критически мыслить.

Исследование, которое проводилось в течение 4-х учебных лет с 7 по 10 класс для двух подгрупп в параллели, показало, что внедрение проблемного обучения и методов развития критического мышления должно быть системным и достаточно длительным процессом. В обеих подгруппах использование проблемных задач и вопросов приводило к различным результатам и требовало более глубокого анализа при выборе методов развития критического мышления. Как показала практика, выбор методов должен основываться на психологический анализ и на дифференциацию в классе. Однако в обеих группах  каждый урок, начиная с проблемной задачи с использованием методов развития критического мышления: «Мозгового штурма», «Обратного мозгового штурма», в течение длительного времени привело к тому, что учащиеся уже на 3-4 четвертый год могли справиться с проблемными задачами, требующие не только глубокие знания, но исследовательские навыки. Успех заключается в том, что урок начинается с проблемы, которая должна быть решена. Проблема, поставленная таким образом, что учащиеся должны получить новые знания, прежде чем они смогут ее решить. Учащиеся не только ищут правильный ответ, а также проводят всесторонний анализ проблемной ситуации, собирают необходимую информацию, определяют возможные решения, оценивают возможные варианты и представляют выводы. При этом правильно организованная деятельность с использованием стратегий критического мышления дает возможность организовать микрообучение и развивать набор мыслительных процессов, включая понимание, анализ, синтез, оценка и рефлексии.

Проблемное обучение, реализованное на уроке на основе методов развития критического мышления, дает возможность построить обучение на следующих принципах (схема 1.):

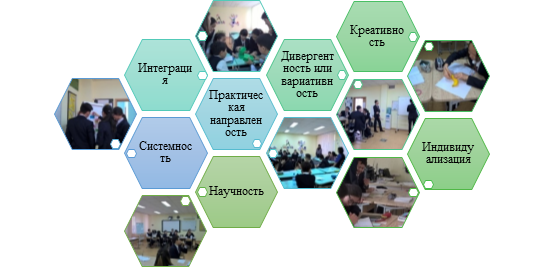
Рисунок 1. Принципы обучения

Проблемные задания помогают учащимся развивать навыки использования математических моделей в повседневной жизни и в различных профессиональных сферах. Системное использование заданий практического и прикладного характера способствует более глубокому пониманию математики в описании процессов и функций в природе. Групповые методы развития критического мышления делают более эффективным, т. к. учащиеся, выдвигая гипотезы и аргументируя, подходят к проблемам с различных сторон, при этом затрагивая большой диапазон знаний.  

Пример.

Метод развития критического мышления: «Зигзаг» (или «Фишбоун», Силовой анализ, Генераторы-критики, Мозговой штурм)

Проблемная задача:

Снежный барс по достоинству считается королем снежных вершин, но носить это гордое звание приходится украдкой, бесшумно и незаметно. Ирбис — очень осторожная кошка, эта особенность не только уберегает ее от встречи с браконьерами, но и не дает ученым возможности определить места постоянного обитания, а значит, и помочь хищнику (Рис.2). [2]

Использование показательных функций для моделирования роста популяций Снежного барса. Если при незначительной эмиграции и иммиграции рождаемость превышает смертность, то популяция будет расти. Рост популяции является непрерывным процессом, если в ней существуют все возрастные группы. Рост популяции при отсутствии каких-либо экологических ограничений описывает показательная функция [1]. В 2014 г. по инициативе Комитета лесного хозяйства и животного мира МСХ РК был разработан План действий по сохранению и изучению снежного барса в Казахстане на 2015-2020 гг. В плане действий, помимо мер направленных на охрану животных, планировалось проведение соответствующих научно-исследовательских работ [3].

Функция, которая может быть использована для моделирования роста популяции на период плана, имеет вид:

.

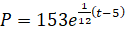• Определить численность популяции через t лет.

• Созданная модель данных используется для прогнозирования роста популяции снежного барса.
• Помогает организовать охрану снежного барса на терретории Казахстана.

Рисунок 2. Снежный барс

Задание: В 2014 году был запущен План действий по сохранению и изучению снежного барса в Казахстане на 2015-2020 гг. Используя математическую модель 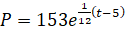 , определите:

• численность снежных барсов в 2020 году. 
• сколько насчитовалость снежных барсов в начале программы?
• Через какое время число снежных барсов достигнет 500?
• Постройте график изменеия численности снежных барсов.

Для определения результативности системного внедрения проблемного обучения и методов развития критического мышления в данном исследовании были использованы результаты мониторинга учебных достижений, который проводился в начале и середине каждого учебного года. Данный мониторинг позволил увидеть уровень сформированности навыков применения и анализа, умения решать задачи на моделирование. Для обработки данных эффективным представлением являются статистические характеристики и графические представления. Исследование, проводимое на основе анализа психологов (по Г.Гарднеру, Дж. Брунеру), анкетирования и наблюдений команды учителей данного класса становится более глубоким, обоснованным и результативным.

Результаты и выводы.

По результатам мониторинга учебных достижений процент выполнения заданий, проверяющих навыки анализа, вырос до 88%, а также повысился процент выполнения на математическое моделирование.

Результаты анкетирования учащихся показали, что все учащиеся считают проблемные задачи и задачи на исследования интересными и очень полезными.

По мнению учащихся "проблемные задачи, требуют поиска знаний", " проблемные задачи, приносят мне пользу в повседневной жизни», "задачи, направленные на исследование, помогают самостоятельно выводить сложные формулы и доказывать теоремы". Однако есть учащиеся, которые написали, что "чувствую не уверенность в заданиях, направленных на исследование». В целом по их мнению, при решении проблемных задач и исследовательских заданий, учащиеся глубоко понимают тему. Наблюдение коллег показало, что учащиеся уже в 9 классе решали исследовательские задачи с уверенностью и уже могли моделировать задачи практического и прикладного характера.

Качество знания к 9-10 классу выросло до 95-100%. А качество знаний за внешнее оценивание в 10 классе составило-95%.

На графическом представлении статистических данных показаны результаты групп по внешнему оцениванию в 10 классе:

Диаграмма «Ящик с усами» показывает, что в обеих группах центральная тенденция смещена к максимальному баллу.

Минимальное среднее значение по двум группам в выборке примерно − 77 баллов.

Нижний квартиль − 25 % выборки набрали в среднем по двум группам меньше 92 баллов.

Медиана − 50 % учащихся показали средний результат по двум группам больше (и меньше тоже) 118.25 балов.

Верхний квартиль − 25 % показали по двум группам выше 135 балов.

И максимальный результат 157 из 160 возможных баллов.

Рефлексия и анализ уроков показали повышение познавательной активности у учащихся. С. Геллерштейн отмечал, что формирование высокого уровня учебных достижений – анализа, синтеза, сравнительной оценки и применение на практике новой информации может быть достигнуто в новых условиях и незнакомых для учащихся ситуациях. И именно такие условия дают возможность создать проблемное обучение и методы развития критического мышления. При обобщении рефлексии уроков с коллегами учащиеся достигли четырех важных результатов:

• учащиеся достигают цели обучения;
• учащиеся формируют навыки анализа, синтеза, оценки и исследования;
• учащихся развивают логическое, критическое и абстрактное мышление;
• учащихся повышают познавательную активность.

А самое главное, возрастает интерес у учащихся к математике.

Следовательно, задания, направленные на исследование и проблемные задания развивают у учащихся мышление высокого порядка, способствуют приобретению глубоких и фундаментальных знаний, а также творческому использованию знаний в практической деятельности, дают мотивацию к достижению успеха.