Методика применения Калейдоскопа «Кванта» в изучении школьного курса математики на примере темы: «Последовательность. Арифметическая и геометрическая прогрессия»

Method of use Kaleidoscope «Quantum» in the study of school mathematics on the example of the theme: «Sequence. Arithmetic and geometric progression»

Shonin Maxim

Graduate student, Moscow University for the Humanities,

math teacher MEI Petropavlovsk School, Russia, Petropavlovsk settlement

Аннотация. В статье дан краткий исторический экскурс создания научного журнала «Квант», его структура. Обосновано его использование в процессе обучения в школе.

Abstract. The article gives a brief historical background of creation of the scientific journal «Kvant». Substantiated its use in the learning process at school.

Ключевые слова: журнал «Квант»; последовательность; арифметическая и геометрическая прогрессия.

Keywords: journal «Kvant»; sequence; arithmetic and geometric progression.

В нашей стране издается много журналов. Они нужны математикам и физикам, биологам и врачам, географам и геологам, инженерам разных специальностей, учителям и, конечно школьникам.

Но своего научного журнала у школьников не было, пока в 1970 году не появился первый научный журнал «Квант» для школьников, интересующихся математикой и физикой.

Первый номер этого журнала вышел в 1970 году, но создание задумывалось несколькими годами раньше. Идею создания такого журнала первый высказал известный физик П.Л. Капица в 1964 году. А первым главным редактором «Кванта», на протяжении почти 15 лет, был выдающийся физик И.К. Кикоин.

Почему этот журнал получил такое название? Так как создатели журнала надеялись, что появление нового журнала вызовет заметный скачек вперед в деле приобщение школьников к современной науке, как идея о том, что электромагнитная энергия поглощается и излучается отдельными порциями – квантами, приложила путь к созданию квантовой механики.

Не сразу сложился современный облик журнала, хотя основные его разделы – общие статьи, «Задачник Кванта», «Лаборатория «Кванта», «Практикум абитуриента», «Информация» - идут с первых номеров.

Позднее появились рубрики «Школа в «Кванте», «Информатика и программирование», «Игры и головоломки», «Квант» улыбается», «Калейдоскоп «Кванта». Всего в журнале более 20 рубрик.

Этот журнал активно можно применить в праздниках юных математиков и физиков, летних лагерях и других интересных мероприятиях. В журнале также можно найти очень много материала, подходящего для работы в школьных кружках. Большая часть журнала рассчитана на старшеклассников, но и ученики 6-7 классов найдут в журнале кое-что интересное. С первых же номеров в «Кванте» публикуются много разнообразных задач. Это задачи в разделах «Квант» для младших школьников», «Избранные школьные задачи», занимательные вопросы, задачи, опыты в «Калейдоскопе «Кванта» и др. Среди рубрик журнала наибольший интерес вызывает у школьников «Калейдоскопе «Кванта», так как именно в ней рассмотрены некоторые интересные школьные вопросы, которые также может использовать учителя математики и физики для подготовке уроков, факультативных занятий.Рассмотрим перечень журналов на предмет темы «Последовательность. Арифметическая и геометрическая прогрессия». По программе эта тема рассчитана на 14-16 часов.

Таблица 1.

Поурочное планирование темы

Изучение темы начинается с непосредственного введения понятия последовательности. При этом можно использовать статьи из номеров: №3 за 1988 год, №9 за 1985 год, №2 за 1995 год, №3 за 1990 год.

Из [3] можно взять определение чисел Фибоначчи и привести как пример бесконечной последовательности. Так как числа Фибоначчи являются элементами числовой последовательности 1, 1, 2, 3, 5…, в которой каждое число, начиная с третьего, является суммой двух предыдущих:  В качестве примера можно рассмотреть и натуральный ряд, некоторые сведения об одном ряде есть в [4], например, термин «натуральное число» впервые был употреблен римским философом Боэцием (ок. 480-524), а стал общеупотребительным после того, как был включен французским математиком Д’ Аламбером (1717-1783) в «Энциклопедию».

А при рассмотрении бесконечной последовательности лучше сказать о том, что она является лишь математическим понятием, удобным обобщением, а не существующим в действительности [1]. Затем вводятся понятия арифметической, геометрической и бесконечно убывающей геометрической прогрессий.

При закреплении этих тем лучше включить задачи с практическим содержанием и старинные задачи, такие как задача о зернах на шахматной доске, задача о семи старцах, задача об исчислении «сложных процентов» и др. Так как именно прикладные и старинные задачи являются одним из приемов зарождения и пробуждения интересов у учащихся к математики. Сам язык, на котором изложен текст задач, смысловая нагрузка пробуждают интерес, любопытство, обостряют внимание, нестандартные ситуации заставляют думать, размышлять. Перед решением таких задач можно дать некоторые исторические сведения. В этом случае поможет [2], где приведены примеры старинных и прикладных задач с их историческими сведениями. Из этой статьи лучше взять и вывод формулы нахождения суммы бесконечно убывающей геометрической прогрессии. Так как он является наиболее простым, чем те способы вывода, которые даны в школьных учебниках, потому что в них доказательство формулы нестрогое, в виду того, что в базовой школе не вводится понятие предела:

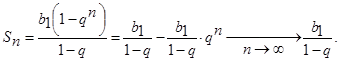
При проведении обобщающего урока можно рассказать о том, что кроме арифметической и геометрической прогрессий существует и гармоническая прогрессия [5].