Автоматизированный расчет. Построение аппроксимирующей функции методом наименьших квадратов по экспериментальным данным химического опыта

AUTOMATED CALCULATION. CONSTRUCTION OF THE APPROXIMATING FUNCTION BY THE LEAST SQUARES METHOD ACCORDING TO THE EXPERIMENTAL DATA OF CHEMICAL EXPERIMENT

Yuliya Astakhova

student, Lipetsk state technical University, Russia, Lipetsk

Anna Polosina

student, Lipetsk state technical University, Russia, Lipetsk

Svetlana Suslova

Cand. tech. Sci., Assoc. Prof., Lipetsk State Technical University, Russia, Lipetsk

Аннотация. В данной статье предлагается разработать алгоритм расчета влияния температуры на скорость гомогенной химической реакции. Для решения задачи применяется линейная аппроксимация.

Abstract. This article proposes to develop an algorithm for calculating the effect of temperature on the rate of homogeneous chemical reaction . Linear approximation is used to solve the problem.

Ключевые слова: химический опыт; температура; скорость; линейная аппроксимация; МНК; Pascal ABC.net; алгоритм в MS Excel.

Keywords: chemical experiment; temperature; velocity; linear approximation; MNK; Pascal ABC.net; algorithm in MS Excel.

Метод аппроксимации находит применение в различных разделах термодинамики и кинетики. Это позволяет упростить обработку результатов и уменьшить число опытов.

Обратимся к понятию аппроксимации.

Аппроксимация – построение такой прямой, для которой отклонения экспериментальных точек от точек прямой находятся в пределах погрешности [1, с. 6].

Рассмотрим применение аппроксимации на конкретном химическом опыте, напишем программу на языке Pascal ABC.net для линейной аппроксимации, найдем ее коэффициенты и значение требуемой величины, характеризующей химическую реакцию, построим аппроксимирующую функцию в Excel методом наименьших квадратов.

Изложим алгоритм нахождения необходимых данных для расчета. Начав с комнатной температуры и постепенно ее увеличивая, определили скорость реакции взаимодействия тиосульфата натрия с серной кислотой.

Получили следующие экспериментальные данные и занесли в таблицу.

n = 8 – количество измерений (таблица 1).

Таблица 1.

Зависимость скорости реакции от температуры

Анализируя экспериментальную зависимость y = f (x), представленную в таблице, видим, что построенные точки (x_i, y_i) на координатной плоскости не оказываются на одной прямой (рисунок 1).

Рисунок 1. Экспериментальные точки

Следовательно, требуется найти такую функцию, которая бы наиболее точно описывала результаты опыта, т. е. проходила так близко к экспериментальным точкам, как только можно.

Поэтому аппроксимируем зависимую переменную величину y = f (x) линейной функцией и получаем y = ax+ b, где a, b – коэффициенты линейной аппроксимирующей функции. Для построения параметров функции  прибегнем к методу наименьших квадратов. Для реализации МНК неизвестные коэффициенты a и b подбираем таким образом, чтобы сумма квадратов отклонений экспериментальных значений y_i от значений, полученных расчетом по аппроксимирующей функции, была минимальной   [1, с. 6].

Выводим формулы для нахождения коэффициентов МНК.

Составляем систему из двух уравнений с двумя неизвестными.

Находим частные производные функции

по переменным а и b, приравниваем эти производные к нулю:

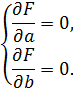
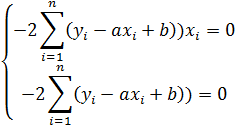
Получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК):

Функция 

 принимает наименьшее значение при полученных значениях a, b.

Формула для нахождения параметра a содержит суммы  ,  ,  , и параметр n – количество экспериментальных данных. Значения этих сумм вычисляем отдельно.

Введем обозначения: = sum1; = sum2;  = sum3; = sum4 .

Находим коэффициенты a и b:

a= n*sum4-sum1 *sum2/n*sum3 -sum1 *sum1

 b= sum2- a*sum1/n.

Реализуем разработанный алгоритм в MS Excel

1. Задаем начальные параметры х_i,у_i (рисунок 2).

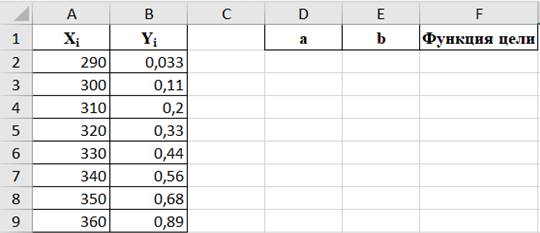
Рисунок 2. Исходные данные

2. В ячейку F2 ввели минимизируемую функцию: =СУММ=((B2:B9+(D2*A2:A9+E2))^2) (рисунок 3).

Рисунок 3. Минимизируемая функция

3. Выбираем команду Поиск решения. Диалоговое окно. Поиск решения заполняем, как показано на рисунке 4. На переменные a и b не налагаются никакие ограничения:

Рисунок 4. Поиск решения

4. В результате вычислений получили a= 0.011902 и b=-3.46408  (рисунок 5).

Рисунок 5. Значения a, b

5. Строим график функции, используя точечную диаграмму с прямыми отрезками и маркерами (рисунок 6).

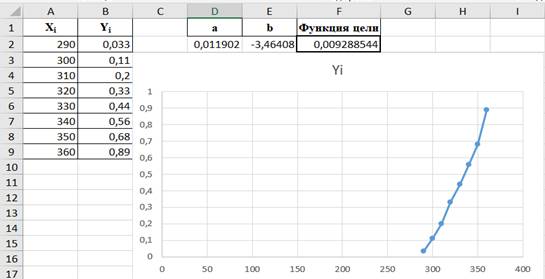
Рисунок 6. График функции

6. Добавляем линию тренда с указанием уравнения функции и величины достоверной аппроксимации (рисунок 7).

Рисунок 7. Линейная аппроксимация

Из графика аппроксимирующей функции, построенного с помощью программы, видно, что чем выше температура, тем выше скорость реакции.

Далее реализуем алгоритм с помощью программного обеспечения Pascal ABC.net.

Введем обозначения переменных:

n – количество известных экспериментальных значений;

x – экспериментальные значения (температура);

y – экспериментальные значения (скорость);

sum1, sum2, sum3, sum4 – суммы;

a, b – коэффициенты аппроксимирующей функции;

x0 – температура, при которой надо найти скорость;

y0 – скорость при заданной температуре.

Программа представлена ниже:

В ходе выполнения программы мы получили следующие результаты: при температуре 303 K скорость химической реакции равна 0,14 c^-1 (рисунок 8).

Рисунок 8. Результаты

Таким образом, мы произвели автоматизированный расчет и выяснили, что метод наименьших квадратов применим для исследования химических экспериментов. С помощью аппроксимирующей функции  можно определить скорость химической реакции при заданной температуре.