РАЗРАБОТКА ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ПОСРЕДСТВОМ ЯЗЫКА PYTHON ДЛЯ ИССЛЕДОВАНИЯ МАКСИМАЛЬНОГО ПОТОКА В СЕТИ

Одной из актуальных задач дискретной математики является задача определения максимального потока в сети. Ее решение непосредственно связано с оптимизацией транспортных путей, сетей трубопроводов, моделированием различных процессов физики и химии, применяется  в коммуникационных и электрических сетях, некоторых операциях над матрицами и для решения родственных задач теории графов. Помимо этого задача может использоваться при составлении расписания авиарейсов, распределении задач в суперкомпьютерах, обработке цифровых изображений и расположении последовательностей ДНК. Программная реализация данной задачи является достаточно востребованной, но при этом не является простой в силу особенностей алгоритмов на графах. В данной работе будет использован алгоритм Форда-Фалкерсона, на котором в течении ряда лет базировалось исследование данной задачи.

Постановка задачи. Транспортная сеть – это ориентированный граф G(E,U), где E – множество вершин графа, U – множество дуг. Основные понятия, т.к. «исток», «сток», «пропускная способность дуги», «поток» и  «насыщенная дуга» даются в [1, с. 236].

Задача о максимальном потоке: необходимо найти такой поток, чтобы величина  принимала максимальное значение [2, с. 363].

Алгоритм Форда-Фалкерсона заключается в итерационном построении максимального потока путем поиска на каждом шаге увеличивающей цепи.

Введем обозначения:

 - символ, обозначающий совпадение ориентации дуги с направлением прохождения цепи;

 - символ, обозначающий противоположную ориентацию дуги по отношению к направлению прохождения цепи;

d(u)=c()-f(),  f*=min f(), d*=min d(), e*=min[f*,d*]

Теорема: Если e*>0, то увеличивая на e* поток на каждой дуге  и уменьшая на e* поток на каждой дуге  цепи, поток f так же увеличивается на e*.

Теорема: Если не существует цепи из источника в сток с e*>0, то поток f нельзя больше увеличить, то есть он максимальный [2, c.366].

Программная реализация алгоритма. Алгоритм реализован на современном высокоуровневом языке программирования общего назначения  Python, который представляет собой достаточно мощный инструмент для создания программ самого разнообразного назначения [3]. Помимо стандартной, достаточно богатой библиотеки языка Python для реализации ПО, была использована библиотека Graphviz, предназначенная для непосредственной визуализации графов.

Продемонстрируем элементы кода программы, представляющие особый интерес.

Листинг 1. Функция bfs(breadth-first search)

Функция bfs(breadth-first search) осуществляет обход графа в ширину [1, c.116]. Алгоритм обхода графа в ширину заключается в последовательном просмотре отдельных «уровней» графа, начиная с вершины-источника.  Вначале посещается источник, затем произвольная вершина, в которую можно попасть из источника,  затем – все потомки данной вершины, далее-все потомки потомков и т.д. Обход графа завершается при достижении нужной вершины, в данном случае - при достижении вершины-стока.

Функция bfs возвращает массив предков, по которому в дальнейшем будет восстановлена цепочка ненасыщенных дуг из вершины источника в вершину-сток.

Листинг 2. Создание и отрисовка графа с помощью библиотеки Graphviz

maxdigraph - нагруженный ориентированный граф, с пропущенным по нему максимальным потоком, т.е. результат решения задачи;

Node - вершины графа, впоследствии соединенные дугами. Для maxdigraph определено n вершин.

Для графа maxdigraph определены три типа дуг:

·     нагруженные. Те, в которых величина пропущенного потока совпадает со значением величины пропускной способности дуги(F=C). будут в дальнейшем обозначены красным цветом(color=”red”);

·     посещенные. Те, через которые был пропущен поток, но он не превышает максимального значения пропускной способности дуги(F<C), обозначены зеленым цветом(color=”green”);

·     не посещенные. Те, через которые был пропущен нулевой поток(F=0), по умолчанию будут черного цвета.

Визуализированный граф сохраняется в виде изображения “maxdigraph.png” и располагается в той же директории, в которой находится исходный код.

Пример решения задачи.  Как правило, использование ПО для решения прикладных задач подразумевает работу с большим объемом входных данных. 

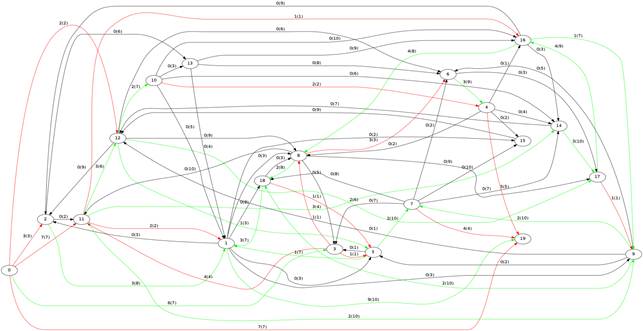
Рисунок 1. Результат работы ПО в произвольном графе на 20 вершин

Рассмотрим результат применения программы к некоторой задаче. Исходные данные - произвольный граф на 20 вершин (Рис.1)

В программный код был добавлен подсчет времени работы программы. На Рис.2 представлен результат подсчета максимального потока в графе с 20-тью вершинами.

Рисунок 2. Время обработки графа с 20-тью вершинами

Язык программирования Python позволил разработать программу, которая решается на ЭВМ достаточно эффективно и может быть использована в дальнейшем для решения прикладных задач.