РАЗРАБОТКА АЛГОРИТМА НЕТОЧНОГО ПОИСКА ЧТЕНИЙ В ГЕНОМЕ ПРИ ИСПОЛЬЗОВАНИИ ВЫЧИСЛЕНИЙ НА ВИДЕОКАРТАХ

Многие современные задачи биологии и медицины требуют знания геномов живых организмов. Изучение генома человека и других живых существ имеет важное прикладное значение. На основании результатов сборки генома конкретного человека возможна реализация персонифицированной медицины — определения предрасположенности человека к различным болезням, создание индивидуальных лекарства и т. д. Кроме этого, на основе результатов исследования геномов растений и животных с использованием методов биоиженерии могут быть выведены новые их виды, обладающие определенными свойствами.

Геном — совокупность наследственного материала, заключенного в клетке организма. Геном содержит биологическую информацию, необходимую для построения и поддержания организма. Большинство геномов, в том числе геном человека и геномы всех остальных клеточных форм жизни, построены из ДНК. В большинстве случаев ДНК состоит из двух полимерных цепочек, состоящих из соединенных в последовательность нуклеотидов. Каждый нуклеотид состоит из азотистого основания, дезоксирибозы и фосфатной группы. Азотистые основания, встречающиеся в ДНК, называются адеин (A), гуанин (G), тимин (T) и цитозин (C). В молекулярной биологии многие объекты представляются в виде последовательности символов. Длина этих последовательностей может достигать миллиарды символов.

Секвенирование биополимеров — определение их аминокислотной или нуклеотидной последовательности. В результате секвенирования получают формальное описание первичной структуры линейной макромолекулы в виде последовательности мономеров в текстовом виде. Данные секвенирования — чтения геномной последовательности. В основном, их длина порядка 100 нуклеотидов, геном покрыт чтениями несколькими десятками раз. Далее из полученных данных и происходит сборка генома. Следует отметить, что в силу множества факторов при чтении даже коротких последовательностей нуклеотидов аппаратные погрешности могу повлечь ошибку. При этом каждое чтение может являться не подстрокой искомой последовательности нуклеотидов, а строкой, слегка отличающейся от нее. Ошибки могут встречаться трех видов: вставки, удаления и замены.

Задача сборки генома является одной из главных задач биоинформатики. На выходе секвенатора мы получаем большой набор небольших чтений, и нам нужно из этих кусочков собрать целый геном. Для решения данной задачи существует несколько подходов. Один из подходов основан на поиске перекрытий чтений, а второй на выравнивание полученных чтений на референсный геном. В обоих этих случаях появляется необходимость неточного сравнения двух строк. Учитывая размер данных, такая задача требует больших объемов вычислений, а поиск неточного вхождения каждого из чтений в геном является независимой подзадачей. Поэтому в своих исследованиях я рассматривала различные модификации алгоритмов, подходящие для решения поставленной задачи, и приспосабливала их для выполнения на графическом процессоре(GPU).

В исследованиях рассматривались различные алгоритмы. Стандартный алгоритм вычисления редакционного расстояния для решения этой задачи предложили Wagner и Fisher. Он использует динамическое программирование и работает за , где w и v — сравниваемые строки. Далее, будут представлены два алгоритма, которые, по сути, работают за линейное время для данной задачи.

Автомат Левенштейна.

Был построен детерминированный универсальный автомат Левенштейна для фиксированного редакционного расстояния n. Были сгенерированы таблицы, содержащие параметры и общее описание состояний и переходов универсального автомата Левенштейна. Необходимо заметить, что таблицы являются универсальными и строятся заранее, никак не завися от входных данных и сравниваемых строк. Во время выполнения, получая входное слово w и слово, с которым его необходимо сравнить v, на основании булевских векторов, являющихся битовыми масками рассматриваемого символа из строки v в подстроке w длины от текущей позиции, совершаются переходы автомате. Таким образом, эмулируется построение детерминированного автомата для конкретного слова w. Время работы алгоритма:.

Были построены таблицы для различных n=0..6. В начале, в глобальную память графического процессора были загружены референсная геномная последовательность, чтения, универсальный автомат Левенштейна (таблица) для заданного n. Далее для каждого из чтений запускался неточный поиск вхождения в геном. Каждому потоку соответствовало одно чтение. Для каждого потока, соответствующему чтению длины k требовалось не более чем k+n обращений к таблице.

Выявленные достоинства метода:

·     Работает за линейное время.

·     Препроцессинг происходит до выполнения. Построение таблиц — отдельная независимая задача.

·     Не теряет в производительности при увеличении длины чтений. Реализация не упирается в ограничения по длине чтений.

Выявленные недостатки метода:

·     Для n > 4 таблицы становятся очень большими, и при n=7 таблица уже не может поместиться в глобальную память видеокарты.

·     Требуется k+n дополнительных обращений к глобальной памяти, которая является довольно медленной.

Bitap.

Алгоритм неточного поиска подстроки, использующий тот факт, что в современных компьютерах битовый сдвиг и побитовое «или» являются атомарными операциями. Высокая скорость работы этого алгоритма достигается за счет битового параллелизма — за одну операцию возможно провести вычисления одновременно над 32 и более битами одновременно. Вычислительная сложность  с крайне малой константой. На предварительную обработку идет порядка  операций и памяти, где ∑ — алфавит. Если же длина шаблона писка не превышает длину машинного слова(в битах), сложность получается , где n — заданное редакционное расстояние.

Этот алгоритм показал себя очень эффективным для решения данной задачи. По условию, длины чтений варьируются от 64 символов до 128. Таким образом, маску каждого чтения можно представить в виде всего двух long long int (каждый по 64 бита). А так как алфавит состоит всего из 4 символов, то чтение будет представляться в виде всего лишь 4 таких масок. Таким образом, в связи с этим алгоритм по сути работает на данной задаче за линейное время.

Выявленные достоинства метода:

·     Работает за линейное время.

·     Выполняет одновременно 64 битовые операции.

·     Манипулирует исключительно логическими операциями, которые очень быстро выполняются на ядрах графического процессора.

·     Не требует обращения в глобальную память.

Выявленные недостатки метода:

·     Плохо масштабируется на более длинные чтения, сильно теряя в производительности. Реализация упирается в максимальную длину чтений.

Результаты исследований.

Оба метода были реализованы. Ниже представлены графики сравнения работы алгоритмов. Так в данных исследованиях рассматривалась производительность алгоритмов неточного поиска вхождений, то этап фильтрации кандидатов для сравнения пропускался. Поиск неточного вхождения чтения в референсный геном запускался с каждой позиции генома.

Для получения следующих двух графиков программа тестировалась на видеокарте NvidiaIon 2. Для получения третьего графика тестирование проводилось на видеокарте Nvidia Tesla C2075.

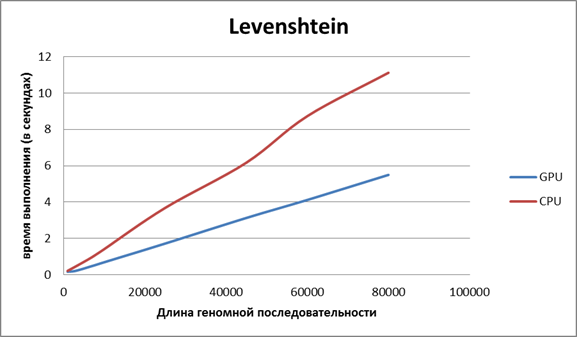
Рисунок 1. Сравнение времени работы алгоритма, использующего автомат Левенштейна, на CPU и GPU

Рисунок 2. Сравнение времени работы алгоритма bitap на CPU и GPU

Рисунок 3. Сравнение алгоритмов Wagner-Fisher, bitap и алгоритма, использующего автомат Левенштейна

Таким образом, были исследованы различные алгоритмы неточного сравнения строк в применении к задаче выравнивания чтений генома, реализация была написана для выполнения на графическом процессоре. Самым эффективным алгоритмом для решения поставленной задачи показал себя алгоритм Bitap.

Список литературы:
1.    Александров А.В., Казаков С.В., Мельников С.В., Сергушичев А.А., Царев Ф.Н., Шалыто А.А. Метод сборки контигов геномных последовательностей на основе совместного применения графов де Брюина и графов перекрытий // Всероссийская научная конференция по проблемам информатики (СПИСОК-2012). СПб.: ВВМ. СПбГУ. 2012, С. 415—418.
2.    Klaus U. Schulz, Stoyan Mihov. Fast String Correction with Levenshtein-Automata // International Journal of Document Analysis and Recognition, 2002.
3.    Mitankin P.N. Universal Levenshtein Automata. Building and Properties // Sofia University St. Kliment Ohridski, 2005.
4.    Udi Manber, Sun Wu. Fast text search allowing errors // Communications of the ACM, 35(10): Р. 83—91, 1992.
5.    Ricardo A. Baeza-Yates, Gastón H. Gonnet. A New Approach to Text Searching // Communications of the ACM, 35(10): Р. 74—82, 1992.
6.    Stephen M. Rumble, Phil Lacroute, Adrian V. Dalca, Marc Fiume, Arend Sidow, Michael Brudno. SHRiMP: Accurate Mapping of Short Color-space Reads // Public Library of Science, 2009.