Расчет искажения напряжения в электроэнергетической системе
Секция: Технические науки

XLIII Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
Расчет искажения напряжения в электроэнергетической системе
Введение. Качество электроэнергии определяется параметрами, описывающими производство и передачу энергии, и характеризующими напряжение в электроэнергетической системе. Искажение формы напряжения отрицательно действует на электрооборудование, вызывает ложные срабатывания систем управления и защиты, сокращает сроки службы изоляции. Применение импульсных схем возбуждения синхронных генераторов ухудшают форму выходного напряжения, при этом возникают дополнительные потери энергии. Актуальны эти вопросы в автономных электроэнергетических системах, когда мощность системы и мощность источника одного порядка [1, с.47–59, 112–134].
Несинусоидальное напряжение характеризуется коэффициентом несинусоидальности, который определяется отношением действующего напряжения высших гармоник к напряжению основной частоты
 , (1)
, (1)
где: ![]() – действующие напряжения основной и высших гармоник.
– действующие напряжения основной и высших гармоник.
Существующие способы расчета ![]() основаны на уравнениях синхронного генератора, которые в общепринятых обозначениях имеют вид [2, с.154–159].
основаны на уравнениях синхронного генератора, которые в общепринятых обозначениях имеют вид [2, с.154–159].
 (2)
(2)
При заданной нагрузке из (2) можно получить изображения составляющих выходного напряжения для любой формы напряжения возбуждения. Затруднением является невозможность получения явного выражения для напряжения на нагрузке даже при простой форме напряжения возбуждения. Развитию этого посвящена работа [3], однако в ней напряжение возбуждения задается в виде гармонической функции, и затруднено получения точного значения ![]() .
.
В пакете MatLab Simulink и в библиотеках Power System имеются средства моделирования синхронных генераторов, которые позволяют получить стационарный режим при различных видах возбуждения, а для визуального исследования состава напряжения применяется спектрограмма [4]. Ввиду учета ограниченного числа гармоник затруднительно получение точного значения ![]() .
.
Целью статьи является разработка методики имитационного моделирования для исследования выходного напряжения и численного определения коэффициента несинусоидальности ![]() синхронного генератора при различных условиях импульсного возбуждения.
синхронного генератора при различных условиях импульсного возбуждения.
Материалы исследований. Преобразуем выражение (1) к виду, в котором действующие значения напряжения и его первой гармоники вычисляются непосредственно по мгновенному значению напряжения ![]()
 , (3)
, (3)
где: ![]() , интеграл в числителе – действующее значение напряжения, а в знаменателе – действующее значение первой гармоники.
, интеграл в числителе – действующее значение напряжения, а в знаменателе – действующее значение первой гармоники.
Введем сопротивление рассеяния обмотки возбуждения ![]() , продольной демпфирующей обмотки
, продольной демпфирующей обмотки ![]() и обмотки фазы статора
и обмотки фазы статора ![]() и перепишем уравнения (2) генератора под резистивно-индуктивной нагрузкой
и перепишем уравнения (2) генератора под резистивно-индуктивной нагрузкой ![]() :
:
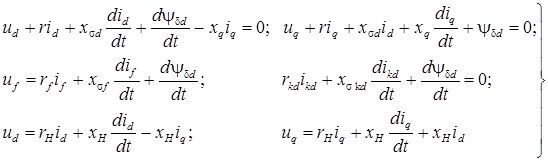 . (4)
. (4)
Потокосцепление в зазоре ![]() по продольной оси вследствие насыщения магнитной цепи нелинейно зависит от намагничивающего тока
по продольной оси вследствие насыщения магнитной цепи нелинейно зависит от намагничивающего тока ![]() . Аналитическое решение этих уравнений невозможно, поэтому для исследования предлагается имитационное моделирование, которое заключается в численном исследовании моделей с помощью существующих программных средств расчета электрических цепей, например, Electronics Workbench [3, 4 ,5].
. Аналитическое решение этих уравнений невозможно, поэтому для исследования предлагается имитационное моделирование, которое заключается в численном исследовании моделей с помощью существующих программных средств расчета электрических цепей, например, Electronics Workbench [3, 4 ,5].

Рисунок 1. Параллельная схемная модель генератора под резистивно-индуктивной нагрузкой
Подобная модель генератора под резистивно-индуктивной нагрузкой, соответствующая уравнениям (4), изображена на рисунке 1. Проводимости: ![]() и
и ![]() численно равны активным сопротивлениям фазы нагрузки
численно равны активным сопротивлениям фазы нагрузки ![]() и фазы статора
и фазы статора ![]() ; проводимости
; проводимости ![]() – активным сопротивлениям обмотки возбуждения
– активным сопротивлениям обмотки возбуждения ![]() и продольной демпфирующей обмотки
и продольной демпфирующей обмотки ![]() . Емкости
. Емкости ![]() численно равны реактивному сопротивлению нагрузки
численно равны реактивному сопротивлению нагрузки ![]() ; емкость
; емкость ![]() – поперечной реактивности генератора
– поперечной реактивности генератора ![]() . Сопротивления рассеяния
. Сопротивления рассеяния ![]()
![]() численно равны емкостям
численно равны емкостям ![]() . Единичная индуктивность
. Единичная индуктивность ![]() предназначена для получения производной от продольного потокосцепления в зазоре
предназначена для получения производной от продольного потокосцепления в зазоре ![]() , которое имитируется управляемым источником тока
, которое имитируется управляемым источником тока ![]() в соответствии с его нелинейной зависимостью от
в соответствии с его нелинейной зависимостью от ![]() . Линейные управляемые источники тока
. Линейные управляемые источники тока ![]() реализуют соотношения
реализуют соотношения ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Источник тока
. Источник тока ![]() численно равен напряжению
численно равен напряжению ![]() . Эта часть модели производит решение системы (4): напряжения на емкостях
. Эта часть модели производит решение системы (4): напряжения на емкостях ![]() численно равны составляющим тока статора; напряжение на
численно равны составляющим тока статора; напряжение на ![]() – току возбуждения; на емкости
– току возбуждения; на емкости ![]() – току в продольной демпфирующей обмотке. Составляющие напряжения
– току в продольной демпфирующей обмотке. Составляющие напряжения ![]() численно равны токам, верхней части рисунка.
численно равны токам, верхней части рисунка.
Контуры ![]() ,
, ![]() ,
, ![]() представляют интеграторы с единичными емкостями и нулевыми начальными условиями для подсчета интегралов в (3). Токи источников
представляют интеграторы с единичными емкостями и нулевыми начальными условиями для подсчета интегралов в (3). Токи источников ![]() в этих контурах равны выражениям подинтегральных функций в (3) соответственно
в этих контурах равны выражениям подинтегральных функций в (3) соответственно ![]() ,
, ![]() ,
, ![]() . Источник
. Источник ![]() вычисляет коэффициент несинусоидальности, который равен напряжению на единичной проводимости
вычисляет коэффициент несинусоидальности, который равен напряжению на единичной проводимости ![]() в момент окончания моделирования. В режиме холостого хода модель упрощается за счет исключения емкостей
в момент окончания моделирования. В режиме холостого хода модель упрощается за счет исключения емкостей ![]() , проводимостей
, проводимостей ![]() и источников тока
и источников тока ![]() .
.
Для расчета ![]() представленные модели выводятся в стационарный режим. Такой режим достигается просчетом их на длительном интервале времени, что требует больших вычислительных ресурсов и приводит к потере точности. Задача определения таких начальных напряжений на емкостях моделей, которые сразу бы обусловили установившийся режим, решается с помощью процедуры минимизации суммы квадратов разностей между значениями напряжений в начале и в конце периода промышленной частоты.
представленные модели выводятся в стационарный режим. Такой режим достигается просчетом их на длительном интервале времени, что требует больших вычислительных ресурсов и приводит к потере точности. Задача определения таких начальных напряжений на емкостях моделей, которые сразу бы обусловили установившийся режим, решается с помощью процедуры минимизации суммы квадратов разностей между значениями напряжений в начале и в конце периода промышленной частоты.
Обсуждение результатов. Для иллюстрации рассмотрен стационарный режим генератора МС117-4 мощностью 125 кВА с параметрами в относительных единицах [3]: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() под резистивно-индуктивной нагрузкой
под резистивно-индуктивной нагрузкой ![]() при возбуждении прямоугольными импульсами амплитудой 0,5 о.е. и частотой 300 Гц.
при возбуждении прямоугольными импульсами амплитудой 0,5 о.е. и частотой 300 Гц.

Рисунок 2. Стационарный режим генератора с импульсным возбуждением под резистивно-индуктивной нагрузкой
На рисунке 2 изображены напряжения и токи этого режима, рассчитанные по модели на рисунке 1 с точностью ![]() %. На графиках рисунка 2 видны искажения продольной составляющей напряжения, соответствующие импульсам напряжения возбуждения; заметны они и в кривой фазного напряжения. Коэффициент несинусоидальности составляет 1,65%.
%. На графиках рисунка 2 видны искажения продольной составляющей напряжения, соответствующие импульсам напряжения возбуждения; заметны они и в кривой фазного напряжения. Коэффициент несинусоидальности составляет 1,65%.

Рисунок 3. Холостой ход генератора с импульсным возбуждением
Для сравнения на рисунке 3 изображены кривые, соответствующие режиму холостого хода генератора, которые показывают наличие существенных импульсных искажений в фазных напряжениях. Эти искажения проявляются вблизи перехода графиков через ноль, что объясняется насыщением магнитной цепи. Коэффициент искажения составляет 2,85%. Таким образом, при малых нагрузках искажения выходного напряжения генератора проявляются более заметно. Подобные же исследования показали снижение коэффициента несинусоидальности с ростом частоты и с соответствующим снижением амплитуды импульсов возбуждения.
Вывод:
Существующие методы анализа искажения фазных напряжений синхронных генераторов при импульсном возбуждении отличаются громоздкими преобразованиями и дают приближенные значения коэффициента несинусоидальности. Достоинством применения предлагаемой методики является повышенная точность определения коэффициента несинусоидальности, так как определение его производится непосредственно по мгновенному значению выходного напряжения генератора. Проведенные исследования показали, что искажения в наибольшей степени проявляются в режиме холостого хода. Повышение частоты импульсного возбуждения снижает искажения фазного напряжения.





