АРМИРОВАНИЕ СПИРАЛЬНО СВЕРНУТЫХ КОНСТРУКЦИЙ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ
Секция: 10. Моделирование

XII Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
АРМИРОВАНИЕ СПИРАЛЬНО СВЕРНУТЫХ КОНСТРУКЦИЙ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ
В работе исследуется влияние углов армирования ткани на напряженно-деформированное состояние спирально армированных оболочек вращения.
Для получения слоистых композитов в качестве армирующих элементов используют ткани на основе высокопрочных волокон различной природы [1].
Отечественной и зарубежной промышленностью выпускаются ткани на основе стеклянных, органических и углеродных волокон, имеющие различное переплетение. Наиболее простая схема — полотняное переплетение, когда каждая нить основы и утка проходит поочередно сверху и снизу пересекающихся нитей. Широко распространенным является сатиновое переплетение, когда каждая нить проходит поочередно сверху, а затем снизу пересекающей ее нити. Более сложным является саржевое переплетение, при котором каждая нить основы и утка проходит поочередно сверху и снизу двух и четырех пересекающих ее нитей. При этом на поверхности ткани образуется структура диагональных линий. Возможны и другие типы переплетений, например трехмерные.
Характерной особенностью рассматриваемых материалов является ярко выраженная анизотропия механических свойств, зависящая от расположения армирующих элементов. Направление армирования задается тремя углами: углом армирования γ, углом к меридиану ψ и углом спиральности α (рисунок 1).
Это обстоятельство позволяет поставить задачу о проектировании оболочек с наиболее рациональной схемой расположения армирующих элементов при заданном виде нагружения.

γ — угол между проекцией направления армирования на плоскость (s,θ) и плоскостью (s,n);
ψ — между проекцией направления армирования на плоскость (s,n) и плоскостью (s,θ);
α — между проекцией направления армирования на плоскость (θ,n) и плоскостью (s,θ).
Рисунок 1. Углы, определяющие направление армирования
Ортогональные в исходном листовом материале армирующие элементы при выкладке располагаются по сложным спиральным траекториям вокруг оси вращения, при этом направляющие косинусы этих элементов являются переменными как по длине, так и по толщине конструкции. Первоначально плоский материал трансформируется в некую линейчатую развертывающуюся поверхность. Это требование обеспечивает возможность выкладки тела вращения из плоских лепестков без складок и разрывов (рисунок 2) . Углы, определяющие направление армирования в готовой конструкции зависят от ориентации выкройки на ткани.

Рисунок 2. Коническая часть заготовки детали
Задача нахождения напряженно-деформированного состояния оболочки решается по алгоритму метода конечных элементов [3] в форме метода перемещений с учетом гипотезы Кирхгофа-Лява, в основу которой положено предположение о том, что после деформации нормаль к координатной поверхности оболочки остается нормальной к деформированной координатной поверхности, прямолинейной и не изменяет своей длины. В качестве неизвестных берутся значения линейных u, v, w и угловых перемещений ![]() и их производные [2].
и их производные [2].
Для построения модели выбран вариационный принцип Лагранжа, позволяющий получить разрешающие уравнения для оболочки на основе минимизации потенциальной энергии, которая может быть выражена через перемещения и упругие константы материала любой схемы армирования
Равновесие оболочки достигается при минимуме потенциальной энергии, для отыскания которого необходимо выразить деформации и перемещения координатной поверхности через узловые переменные.
В тестовой задаче было исследовано влияние параметров армирования на напряженно-деформированное состояние конической части заготовки детали под воздействием нормальной нагрузки. Расчетная схема задачи приведена на рисунке 3. Физико-механические характеристики материала принимались равными Е=6000 кгс/мм2, ν=0,12, α=7∙10-7 К-1.
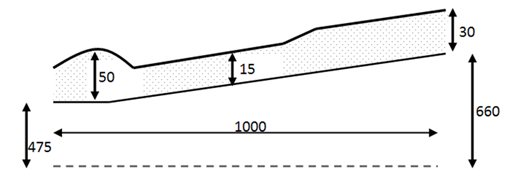
Рисунок 3. Расчетная схема
На рисунке 3 представлены зависимости прогибов от меридиональной координаты при различных углах ориентации лепестка к основе ткани при равномерно-распределенном нормальном давлении 15 Мн/м2.
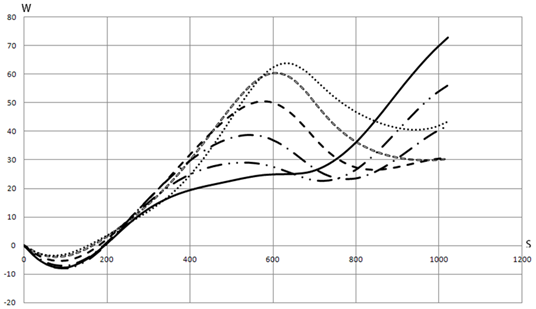
Рисунок 3. Перемещения при разных углах ориентации выкройки к основе при нагрузке qn=15 МН/м2:
![]() угол 100
угол 100
![]() угол 200
угол 200
![]() угол 300
угол 300
![]() угол 400
угол 400
![]() угол 500
угол 500
![]() угол 600
угол 600
Поведения кривых зависимостей прогибов от меридиональной координаты качественно изменялось с изменением угла ориентации лепестка к основе ткани. При начальном угле установки в 100наблюдается рост функции и наибольшее значение прогиба достигается на правой кромке конструкции. При углах в 200 и 300 рост функции продолжаетсядо отметки ≈500 S, далее спад до ≈750 S и вновь рост до достижения наибольшего значения на правой кромке.Начиная с 400, наибольшее значение прогиба с кромки перемещается на участок в ≈600 S.
Таким образом, построенная модель позволяет проводить исследования по подбору рациональной схемы армирования для проектирования конструкций с заданными жесткостными характеристиками.
Список литературы:
1. Васильев В.В. Прочность цилиндрических оболочек из армированных материалов [Текст] / Васильев В.В., Елпатьевский А.Н. — М.: Машиностроение, 1972 г. — 168 с.
2. Еременко С.Ю. Методы конечных элементов в механике деформируемых тел [Текст] / С.Ю. Еременко — Харьков: изд. «Основа» при Харьк. гос. ун-те, 1991. — 272 с.
3. Сегерлинд Л. Применение метода конечных элементов [Текст] / Л. Сегерлинд. — М.: Мир, 1979. — 392 с.





